Come ricavare l`espressione matematica dell`accelerazione

Come ricavare l'espressione matematica
dell'accelerazione centripeta
Data un moto circolare uniforme di raggio r e di
velocità costante v dedurremo la legge che descrive
l'accelerazione centripeta, e di conseguenza della forza
centrifuga.
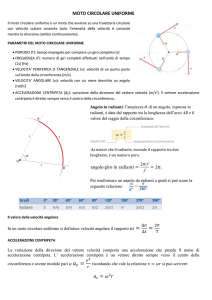
Abbiamo quindi un moto circolare (come nel disegno).
Vediamo, nella figura, il segmento P 1 P 2 che è lo spazio
percorso dal punto materiale con velocità tangenziale v
nel tempo t . Possiamo mettere in relazione i segmenti
con il teorema di Pitagora. Quindi:
Dalla relazione [F1], se sviluppiamo il binomio e
r h2=v⋅t 2r 2 [F1]
eleviamo alla seconda potenza troviamo [F2],
2
2
2 2
2
semplificando r 2 e raccogliendo h troviamo
r 2⋅h⋅rh =v ⋅t r [F2]
[F3].
2 2
Adesso possiamo osservare che, se t  0 (t
h 2r h=v t [F3]
tende a 0) allora h≪ r (h sarà molto minore di
r) e di conseguenza 2r h≈2r , quindi
2 2
possiamo ottenere [F4]. Da quest'ultima relazione
2rh≈v t [F4]
troviamo h [F5].
Se si osserva bene si nota che se confrontiamo
1 v2
h≈   t 2 [F5]
[F5] con l'equazione oraria di un moto
2 r
uniformemente accelerato possiamo dedurre
l'accelerazione [F6].
v2
[F6]
ac=
r
Conseguenze
Da questa relazione possiamo dedurne altre due; quella della forza centripeta (o centrifuga) e quella
dell'accelerazione espressa con la velocità angolare.
1. Forza Centripeta
{
 =m
F
a
[F7]

v2
ac =
r
Se mettiamo a sistema le due relazioni
(accelerazione centripeta e secondo principio di
Newton) otteniamo la forza centripeta [F8].
2
 =m v [F8]
F
r
2. Forza e accelerazione centripeta in funzione della velocità angolare
{
⋅
 r =v
[F9]
v2
ac =
r
 2⋅r [F10]
ac =
Se mettiamo a sistema l'accelerazione centripeta
con la definizione di velocità in un moto circolare
uniforme troviamo [F10]. Se vogliamo la forza
centripeta basta seguire lo stesso procedimento
del punto precedente e quindi ottenere [F11].
 2⋅r [F11]
F c =m⋅
Bibliografia
Invito alla fisica vol.1 Paul A. Tipler Zanichelli 1990