Cinematica – Soluzioni

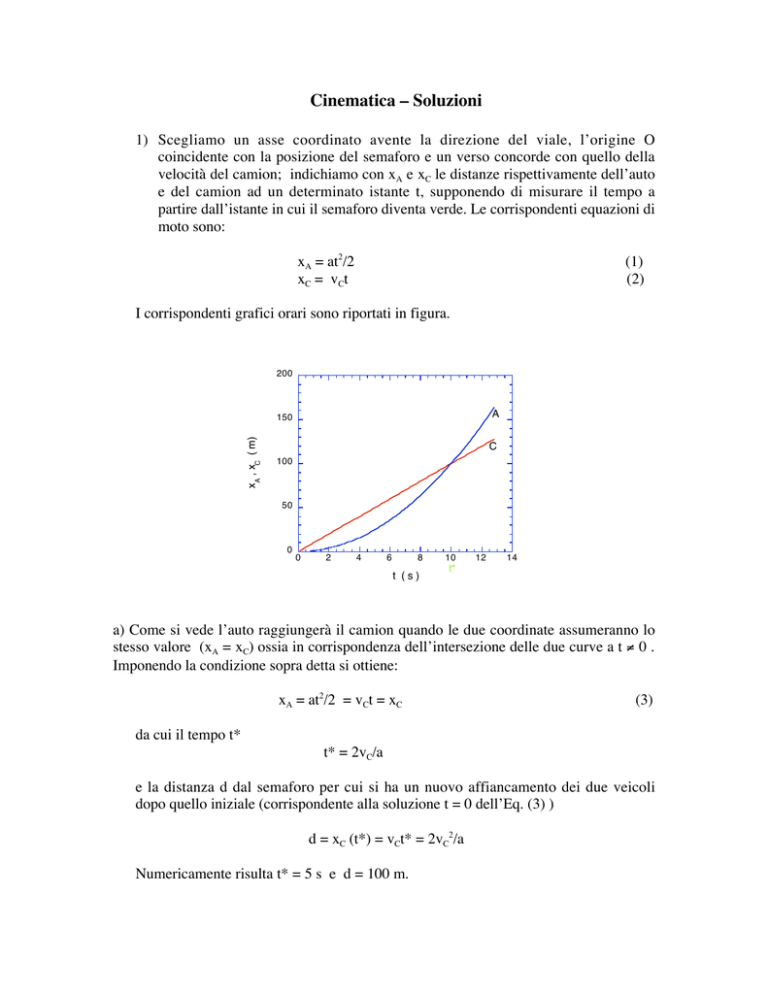
Cinematica – Soluzioni
1) Scegliamo un asse coordinato avente la direzione del viale, l’origine O
coincidente con la posizione del semaforo e un verso concorde con quello della
velocità del camion; indichiamo con xA e xC le distanze rispettivamente dell’auto
e del camion ad un determinato istante t, supponendo di misurare il tempo a
partire dall’istante in cui il semaforo diventa verde. Le corrispondenti equazioni di
moto sono:
xA = at2/2
xC = vCt
(1)
(2)
I corrispondenti grafici orari sono riportati in figura.
200
A
x A , xC ( m)
150
C
100
50
0
0
2
4
6
8
t (s)
10
12
14
t*
a) Come si vede l’auto raggiungerà il camion quando le due coordinate assumeranno lo
stesso valore (xA = xC) ossia in corrispondenza dell’intersezione delle due curve a t ≠ 0 .
Imponendo la condizione sopra detta si ottiene:
xA = at2/2 = vCt = xC
(3)
da cui il tempo t*
t* = 2vC/a
e la distanza d dal semaforo per cui si ha un nuovo affiancamento dei due veicoli
dopo quello iniziale (corrispondente alla soluzione t = 0 dell’Eq. (3) )
d = xC (t*) = vCt* = 2vC2/a
Numericamente risulta t* = 5 s e d = 100 m.
b) L’equazione oraria della velocità dell’auto è data da vA = at , quindi la sua velocità
nell’istante del sorpasso è data da
vA* = at* = 2vC
numericamente quindi si ha vA*= 20 m/s (72 Km/h).
[Osservazione: essendo all’istante t* nuovamente affiancati, i due veicoli devono
avere durante questo intervallo di tempo la stessa velocità media, pari a vc. Dato che
in un moto uniformemente accelerato la velocità media fra due istanti qualsiasi è la
media aritmetica delle velocità nei due istanti, si poteva anche scrivere la relazione:
vAM = vC = [vA (t = 0) + vA*]/2 = vA*/2
da cui il risultato trovato.]
2) Scegliamo un asse coordinato diretto lungo la verticale, orientato positivamente
verso l’alto e con l’origine O coincidente con il punto da cui viene lanciata la
palla, e misuriamo il tempo a partire dall’istante di lancio. La palla si muove di
moto uniformemente accelerato e le equazioni orarie per la velocità e la
coordinata della palla sono:
v = v0 – gt
(1)
x = v0t – gt2/2
(2)
5
0
0
-5
-5
-10
0
0.5
1
1.5
t(s)
2
-10
2.5
( m/s )
5
v ( m/s )
10
abs( v )
x (m)
10
In figura sono riportati il grafico orario per x , v (linea tratteggiata) e per il suo valore
assoluto (linea continua).
a) La palla raggiunge la massima quota quando si annulla la sua velocità, pertanto
dalla Eq. (1) si ottiene il tempo impiegato t* ponendo v = 0 :
t* = v0/g
t* = 1.02 s
b) La massima quota raggiunta corrisponde al valore della coordinata x per t = t*,
quindi da (2) si ha:
H = x(t*) = v02/2g
H = 5.09 m
c) Il tempo t’ che impiega la palla per tornare al punto di partenza lo si ottiene dalla
Eq. (2) ponendo x = 0 ; la soluzione t = 0 corrisponde all’istante di partenza,
mentre per t’ si ha.
t’ = 2v0/g = 2t*
t’ = 2.04 s
d) La velocità quando la palla torna al punto di partenza è ottenuta immediatamente
ponendo nell’Eq. (1) t = t’ e si ottiene:
v = v0 - gt’ = - v0
e) Eliminando il tempo fre le Eq. (1) e (2) si può esprimere la velocità della palla in
funzione della sua coordinata e si ottiene:
v2 = 2gx - v02
v = ± (2gx - v02)0.5
Come risulta dalla precedente espressione ( si veda anche il grafico ) la velocità della
palla può assumere per una stessa quota due valori uguali in modulo ed opposti in
verso in corrispondenza della fase ascendente e discendente del moto. Ponendo x =
H/2 (rappresentato in figura dalla retta orizzontale tratteggiata) si ottiene v = ± 9.38
m/s.
f) Consideriamo i due istanti t e t+Dt e le corrispondenti coordinate della palla x(t) e
x(t+Dt); la differenza fra le due posizioni è data, in modulo e segno, da Dx =
x(t+Dt) - x(t) e risulta esplicitamente:
Dx= (v0 - gt)Dt – g(Dt)2/2 = v(t)Dt – g(Dt)2/2
quindi per due istantanee successive al tempo nDt e (n + 1)Dt si ha:
Dx= v0Dt – g(2n+1)(Dt)2/2
la distanza fra due posizioni successive della palla è quindi data da Dd = abs(Dx) ;
come risulta da questa espressione Dd decresce gradualmente all’avvicinarsi della
palla alla sommità della traiettoria per poi tornare ad aumentare nuovamente una volta
che inizia a muoversi verso il basso ( nella figura l’ordinate dei pallini corrispondono
alle posizioni della palla a intervalli di 0.1 s). Nella figura successiva sono riportati i
valori di Dx(n) in funzione del numero d’ordine n dell’istantanea.
1.4
1.2
Dx ( m )
1
0.8
0.6
0.4
0.2
0
0
5
10
15
20
25
n
3) Scelto l’asse coordinato coincidente con il binario, con l’origine O nel punto in
cui si trova il treno A quando il macchinista inizia a frenare, ed orientato nel verso
di marcia dei treni, le loro equazioni orarie risultano:
xA = v0At – at2/2
xB = d – vBt
dove con -a si è indicato la decelerazione del treno A. I corrispondenti grafici sono
riportati in figura per due diversi valori di a.
700
700
A
x A ( m)
xB ( m )
600
600
500
500
B
A
400
400
300
300
200
200
100
100
0
0
-100
-100
0
5
10
15
t (s)
20
25
Come si vede a seconda della grandezza della decelerazione si ha o meno un’intersezione
fra i due grafici orari ed essa corrisponde all’eventuale collisione. Imponendo quindi la
condizione xA = xB dalle due precedenti equazioni si ricava:
xA = v0At – at2/2 = d – vBt = xB
da cui per l’istante di collisione t* (si scarta ovviamente la radice di valore maggiore):
t* = {(v0A – vB) - [(v0A – vB)2 –2ad]0.5}/2
Perché vi sia effettivamente un impatto t* deve risultare reale, quindi se il termine
sotto radice quadrata è minore di zero la collisione non avviene. Imponendo questa
condizione si ottiene il minimo valore di a necessario ad evitare lo scontro:
a > a* = (v0A – vB)2/2d
ovvero numericamente a* = 0.906 m/s2.
4) Scegliamo un asse coordinato verticale, orientato positivamente verso l’alto e con
l’origine sul fondo del pozzo; misurando i tempi a partire dall’istante in cui si
abbandona il sasso dalla sommità del pozzo, detta h la quota corrispondente, si
per l’equazione oraria del sasso:
y = h - gt2/2
a) Dalla precedente equazione si ricava immediatamente la profondità
imponendo che per t = t* il sasso abbia raggiunto il fondo del pozzo,
corrispondente a y = 0. Si ha:
h = gt*2/2
h = 122 m
(1)
b) Il valore ora trovato non è corretto se teniamo conto che il suono si
propaga con una velocità finita e quindi che il tempo misurato t* è in
realtà la somma del tempo tc che il sasso impiega effettivamente a
raggiungere il fondo e del tempo ts che il suono (prodotto dall’urto del
sasso ) impiega per giungere dal fondo alla cima del pozzo. Scriveremo
pertanto le seguenti relazioni che legano fra loro h ed i tempi considerati:
h = g tc2/2
h = vs ts
tc + ts = t*
Eliminando nelle precedenti equazioni tc e ts si ottiene l’equazione:
h2 – 2h(vst* + vs2/g) + (vst*)2 = 0
da cui
h = (vst* + vs2/g) – [(vst* + vs2/g)2 - (vst*)2]0.5
che fornisce il valore numerico h = 107 m.
c) Se l’operatore arresta il cronometro con un ritardo t , il tempo
effettivamente impiegato dal sasso a cadere (trascurando la velocità del
suono) sarà t’ = t*- t. La relazione corretta risulta quindi data da:
h = gt’2/2
da cui l’errore che si commette assumendo t* come tempo effettivo di caduta
Dh = gt*2/2 – gt’2/2 = gt*t - gt2/2
Numericamente risulta Dh = 4.85 m , e come si vede un piccolo ritardo nell’arresto
del cronometro comporta un errore (per eccesso) non trascurabile nella
determinazione di h.
5) Scegliamo un asse coordinato diretto lungo la verticale ascendente con l’origine 0
in corrispondenza del davanzale della finestra da cui si osserva. Indichiamo con h
la quota, incognita, del punto da cui cade l’oggetto e scegliamo come istante
iniziale quello di inizio della caduta. Il corpo si muove di moto uniformemente
accelerato sotto l’azione della gravità; la sua equazione di moto è pertanto:
y = h - gt2/2
y
Se indichiamo con t’ il tempo che l’oggetto impiega
per arrivare al limite superiore della finestra ( y = l)
e di conseguenza con ( t’ + t ) il tempo impiegato
per arrivare al davanzale (y = 0 ), avremo dall’equazione di moto le due relazioni:
l = h – gt’2/2
h
0 = h - g(t’ + t)2/2
Queste due equazioni consento di determinare i
valori incogniti di t’ ed h ; risolvendo per quest’ultimo si ottiene:
h = [ 1 + l/gt2 + gt2/4l ]l/2
l
O
e numericamente h = 8.78 m.
6) Le accelerazioni medie dei due veicoli sono determinate immediatamente
applicando la definizione, e si ottiene:
a1 = 1.91 m/s2
a2 = 6.17 m/s2
a1 = V/T1
a2 = V/T2
I corrispondenti spazi percorsi nella fase di accelerazione sono dati da:
s1 = a1T12/2 = VT1/2
s2 = a2T22/2 = VT2/2
s1 = 62.5 m
s2 = 201.4 m
(Osservazione: nelle due precedenti relazioni lo spazio percorso è espresso come il
prodotto della velocità media per il tempo. In un moto uniformemente accelerato la
velocità media vm in un intervallo di tempo in cui la velocità passa dal valore v1 al
valore v2 è facilmente calcolabile essendo data dalla media aritmetica dei due valori,
ossia da:
vm = (v1 + v2)/2
Ovviamente quest’ultimo risultato vale soltanto per un moto uniformemente
accelerato. )
7) Consideriamo un asse coordinato nella direzione di marcia del veicolo e con lo
stesso verso; poniamo l’origine nel punto in cui si trova il veicolo all’inizio della
frenata e corrispondentemente fissiamo l’istante iniziale. Le equazioni orarie
corrispondenti a questo moto uniformemente accelerato sono:
x = v0t - at2/2
v = v0 – at
dove v0 è la velocità del veicolo all’inizio della frenata. Da queste, eliminando fra le
due il tempo, si ottiene una relazione diretta fra la posizione, l’accelerazione e le
velocità:
a = (v02 – v2 )/2x
a) Ponendo in questa relazione v = 0 ed x = s si ricava immediatamente
l’accelerazione media:
a= v02/2s
a = 4.96 m/s2
b) La precedente espressione mostra come, a parità di accelerazione, lo spazio di
frenata cresca quadraticamente con la velocità iniziale del veicolo, quindi per una
velocità v’0 = 27.78 m/s ( 100 Km/h) si ha:
s’ = v02/2a
s’ = 77.78 m
c) Se teniamo conto del tempo di reazione complessivo vi è una prima fase del moto
, di durata t , in cui il veicolo si muove di moto rettilineo uniforme con velocità
pari a v0, seguito dalla fase di frenata. Quindi lo spazio totale di arresto diviene:
s* = v0t + s
s* = 44.7 m
Nel caso in cui la velocità sia v’0 lo spazio di frenata divene:
s’* = v’0t + s’
s’* = 105.5 m
8) Indichiamo con t la durata dell’urto, misurata a partire dal contatto della
macchina col muro, e con a l’accelerazione media; dalle equazioni orarie per la
velocità e lo spazio si ottiene al termine dell’urto ( ossia per t = t ):
v(t = t ) = 0 = v0 – at
d = v0t - at2/2
dove v0 è la velocità iniziale del veicolo. Risolvendo per a e t si ottiene:
a= v02/2d
t = v0/a
a = 321.5 m/s2 ª 33 g
t = 43 ms
9) Si scelga un asse di riferimento verticale, orientato positivamente verso l’alto e
con l’origine al livello del suolo, e si misuri il tempo a partire dall’istante di
distacco della goccia. Le equazioni orarie per una goccia, soggetta solo
all’accelerazione di gravità, sono:
v = -gt
y = h - gt2/2
Da queste si può ricavare immediatamente la velocità della goccia, quando essa
raggiunge il suolo, vs = v(y = 0):
vs = (2gh)0.5
v = 140 m/s = 504 km/h
Il tempo impiegato ad arrivare a terra è in questo caso pari a:
ts = (2h/g)0.5 = 2h/vs
ts = 14.3 s
Da confrontare con il tempo che impiega muovendosi con velocità costante:
t0 = h/v0
t0 = 153.8 s
[ Osservazione - La velocità così calcolata è ovviamente irrealistica, la
determinazione corretta del moto della goccia deve tener conto della resistenza
dell’aria comme illustrato nel successivo esercizio 10). ]
10) Si scelga un asse di riferimento verticale, orientato positivamente verso l’alto e
con l’origine al livello del suolo, e si misuri il tempo a partire dall’istante di
distacco della goccia.
a) La goccia è soggetta ad una accelerazione diretta verso il basso data da:
a = - g - Kv
La velocità limite, costante, viene raggiunta quando si annulla l’accelerazione ossia
quando
g + Kv = 0
da cui posto v = -v0 si ha K = g/v0 ossia K = 1.51 s-1.
b) In modo analogo al precedente caso si ha quando la goccia ha raggiunto la velocità
limite v = - v0:
a* = - g + Kv02 = 0
da cui K = g/v02 ossia K = 2.32 m-1.
c) L’equazione di moto della goccia nel caso a) è data da:
a = dv/dt = - (g + Kv)
(1)
La derivazione delle equazioni orarie per la velocità e la posizione della goccia deve
essere fatta integrando l’Eq. (1); separando le variabili si ottiene:
Kdv/( g + Kv ) = - Kdt
Integrando direttamente questa equazione, membro a membro, fra l’istante iniziale (t
= 0 ) e l’istante generico t in cui la velocità vale rispettivamente v = 0 e v(t) si
ottiene:
v(t ) Kdv'
t
Ú 0 g + Kv' = -K Ú 0 dt'
da cui
†
ln( 1 + Kv(t)/g) = -Kt
e infine invertendo il logaritmo:
v = v(t) = - (g/K)[1 – exp(-Kt)] = - v0[1 – exp(-Kt)]
(2)
Si vede quindi che la velocità si avvicina esponenzialmente al valore limite v0 con
una costante di tempo pari ad (1/K).
[NOTA: dicesi “costante di tempo”, relativa ad un andamento esponenziale di una
grandezza fisica, il tempo in cui l’esponenziale passa dal valore iniziale ( = 1 ) al
valore 1/e ].
L’equazione oraria può essere ottenuta per integrazione diretta dell’Eq. (2), infatti si
ha:
v = dy/dt = - v0[1 – exp(-Kt)]
e, separando le variabili:
dy = - v0[1 – exp(-Kt)]dt
integrando direttamente fra l’stante iniziale ( t = 0 , h = 0 ) e l’istante generico t ( y =
y(t) ) si ottiene:
Ú
y(t )
h
t
dy = -v 0 Ú 0 [1- exp(-Kt')]dt'
da cui
y – h = - v0t + (v0/K)[1 – exp(-Kt)]
(3)
†
I corrispondenti
andamenti per il modulo della velocità e per la coordinata sono
riportati nelle figure in fondo all’esercizio ed indicati con la lettera c . Nel grafico
della velocità è riportata anche la retta v = 0.9v0 la cui intersezione con la funzione v
= v(t) fornisce il valore di t = t’ per cui si raggiunge il 90% della velocità limite. Nel
grafico della coordinata è riportata la retta t = t’ la cui intersezione con la funzione y
= y(t) fornisce la distanza percorsa dalla goccia all’istante considerato; si noti che
dopo tale istante il moto può essere considerato con buona approssimazione rettileo
uniforme.
La goccia quindi raggiungerà una velocità v = - 0.9v0 dopo un tempo t’ il cui valore si
ottiene immediatamente dall’Eq. (2):
v = - 0.9v0 = - v0[1 – exp(-Kt’)]
da cui:
t’ = - (1/K)ln(1 – v/v0) = ln(10)/K
t’ = 1.52 s
La distanza Dy percorsa dalla goccia nel tempo t’ è calcolata immediatamente dall’Eq. (3)
ponendo t = t’ e si ha:
Dy = h – y(t’) = v0t’ - (v0/K)[1 – exp(-Kt’)] = v0t’ - 0.9v0/K = v0t’ - 0.9v02/g
da cui Dy = 6 m.
d) In questo caso l’equazione di moto è data da:
dv/dt = a* = - g + Kv2 = - g[1 – (v/v0)2]
dove si è tenuto conto dell’espressione di K = g/v02.
Anche in questo caso separando le variabili e riordinando i termini si ottiene:
dv/v0[1 – (v/v0)2] = -(g/v0)dt
Questa equazione può essere integrata direttamente fra l’istante iniziale ( t = 0, v = 0) e
l’stante generico t ( v = v(t)):
Ú
v(t )
0
1
dv'
g t
=
-(
) Ú dt'
v0 0
1- ( v' v ) 2 v 0
0
da cui
ln[(1 + v/v0)/( 1 – v/v0)] = -2(g/v0)t
(4)
† il logaritmo:
ossia invertendo
v = v(t) = - v0tgh(gt/v0)
(5)
Anche in questo caso la velocità limite viene raggiunta asintoticamente con una costante
di tempo dell’ordine di v0/g = 1/(Kg)0.5.
Dall’Eq. (5) si puo infine ottenere l’equazione oraria, infatti risulta:
v = dy/dt = - v0tgh(gt/v0)
Da questa separando le variabili si ottiene:
dy = - v0tgh(gt/v0)dt
che integrata fra l’stante iniziale t = 0 ( y = h ) e l’stante generico t ( y = y(t) ) fornisce:
Ú
y(t )
0
dy'= -v 0 Ú 0 tgh( gt' v )dt'
t
0
da cui
y – h = - (v02/g)ln[cosh(gt/v0)]
(6)
†
I corrispondenti andamenti
per il modulo della velocità e per la coordinata sono riportati
nelle figure in fondo all’esercizio ed indicati con la lettera d . Nel grafico della velocità è
riportata anche la retta v = 0.9v0 la cui intersezione con la funzione v = v(t) fornisce il
valore di t = t* per cui si raggiunge il 90% della velocità limite. Nel grafico della
coordinata è riportata la retta t = t* la cui intersezione con la funzione y = y(t) fornisce la
distanza percorsa dalla goccia all’istante considerato; si noti che dopo tale istante il moto
può essere considerato con buona approssimazione rettileo uniforme.
Il tempo t* per cui la goccia raggiunge il valore v = - 0.9v0 è ottenuto immediatamente
dall’Eq. (4) e risulta t* = v0ln(19)/2g ossia numericamente t* = 0.97 s.
La distanza percorsa la si ottiene invece dall’Eq. (6) per t = t* e si ha:
Dy = h – y(t+) = (v02/g)ln[cosh(gt*/v0)]
Dy = 3.54
7
7
d
6
6
0.9 v 0
v ( m/s )
c
5
5
4
4
3
3
2
2
1
1
0
0
0
1
2
3
4
5
t(s)
1005
1005
1000
1000
t*
995
t'
y (m)
995
990
990
c
985
985
d
980
980
0
0.5
1
1.5
2
t (s)
2.5
3
3.5
4
[ N.B. Il procedimento adottato per la soluzione dei punti c) e d) è esemplificativo del
metodo di soluzione che deve essere utilizzato nel caso generale: come si vede si procede
per integrazioni successive delle equazioni differenziali per la velocità e per la posizione.
La determinazione completa dell’equazione oraria implica la conoscenza della velocità e
della posizione (oppure di due posizioni) dell’oggetto a due istanti determinati.
Osservazione. Le due espressioni adottate per la resistenza viscosa del mezzo
corrispondono alle sue due schematizzazioni classiche la cui aderenza alla realtà dipende
da molteplici fattori. Senza entrare in dettagli si può dire che, in linea generale, la
schematizzazione utilizzata al punto d) meglio si adatta al caso di una goccia, o di un
altro corpo (naturalmente varierà K ), che cade in aria. Sempre a grandi linee la
schematizzazione del caso c) è invece più aderente al caso di una goccia di olio ( o di un
altro corpo ) che si muove in un acqua.]
11) Nel piano del moto del corpo scegliamo un sistema di riferimento con l’origine O
nel punto da cui esso viene lanciato, l’asse x diretto lungo l’orizzontale nel verso
della componente orizzontale della velocità e con l’asse y verticale e diretto verso
l’alto; si sceglie come istante iniziale quello del lancio del corpo. Dette v0x =
v0cosq e v0y = v0sinq le componenti della velocità di lancio, le equazioni orarie,
lungo i due assi, per la velocità sono:
vx = v0x = v0cosq
vy = v0y – gt = v0sinq - gt
(1)
(2)
Per le coordinate del corpo si hanno le equazioni orarie:
x = v0xt = (v0cosq)t
y = v0yt - gt2/2 = (v0sinq)t - gt2/2
70
60
x , y ( m)
50
40
30
20
10
0
0
1
2
3
t (s)
4
5
(3)
(4)
Nella figura precedente sono riportate i diagrammi orari per le coordinate x ed y
corrispondenti agli angoli di lancio q = p/6 (linea continua), q = p/4 (linea tratteggiata) e
q = p/3 (linea con pallini). Le gittate raggiunte per i diversi angoli sono indicate dalle
frecce.
Le Eq. (3-4) forniscono la traiettoria del corpo in forma parametrica, in cui il parametro è
il tempo, ed eliminado t fra di esse si ottiene l’equazione della traiettoria che come è noto
è una parabola passante per O:
y = xtgq - gx2/2(v0cosq)2 = xtgq - g(1 + tgq2)x2/2v02
(5)
Nella figura seguente sono riportate le tre traiettorie corrispondenti agli angoli di lancio q
= p/6 (linea continua), q = p/4 (linea tratteggiata) e q = p/3 (linea con pallini).
30
25
y (m)
20
15
10
5
0
0
10
20
30
40
50
60
70
x (m)
Le Eq. (1-5) consentono di rispondere a tutte le domande formulate nel testo.
a) La gittata, ossia la distanza da O del punto in cui cade il corpo, la si ottiene
immediatamente dall’Eq. (5) ponendo in essa y = 0 : l’equazione così ottenuta
x[tgq - gx/2(v0cosq)2] = 0
ammette due radici che corrispondono all’intersezione della traiettoria con l’asse delle
ascisse, corrispondente al suolo. La prima radice, x = 0 , corrisponde ad O ossia al
punto di lancio del corpo, l’altra è quella che ci dà la gittata e risulta:
x = 2v02sinqcosq/g = v02sin2q/g
Da questa relazione si ottiene immediatamente che la gittata massima x* viene
raggiunta con un angolo q = b = p/4 e risulta x* = v02/g ; numericamente si ha x* =
63.7 m.
b) Il tempo t* che il corpo impiega per toccare terra nel punto x = x* lo si ottiene
dall’Eq. (3) per x = x* e si ha:
t* = x*/(v0cosb) = v0/(gcosb)
t* = 3.6 s
c) Le componenti della velocità nell’istante dell’impatto t = t* sono fornite
immediatamente dalle Eq. (1-2) e risulta:
vx = v0x
vy = - v0y
Pertanto il modulo della velocità è esattamente uguale a v0 , cioè quello che ha il
corpo al momento del lancio, e l’unica differenza sta nel cambiamento di segno della
componente verticale della velocità.
d) Il punto più alto della traiettoria viene raggiunto quando la componente verticale
della velocità si annulla, ossia all’istante t’ dato dall’equazione:
vy = v0y – gt = v0sinb - gt = 0
ossia per t’ = v0sinb/g = v0/2gcosb = t*/2 . Il risultato poteva anche essere scritto
immediatamente tenendo conto che il vertice della parabola si trova esattamente nel
punto intermedio fra l’origine O ed il punto di impatto.
Per quanto riguarda la velocità risulta immediatamente che, essendo nel vertice vy = 0
, essa è orizzontale ed essendo questa componente costante nel tempo essa è pari a
v0cosb.
La quota massima raggiunta dal corpo corrisponde giusto all’ordinata y’ del vertice
della parabola e si ottiene immediatamente dall’Eq. (4) per t = t’ ( oppure dall’Eq. (5)
per x = x*/2 ):
y’ = (v0sinb)2/2g
y’ = 15.93 m
12) L’equazione della traiettoria di un proiettile sparato con un alzo q e velocità v0 è
data dell’Eq. (11-5):
y = xtgq - gx2/2(v0cosq)2 = xtgq - g(1 + tgq2)x2/2v02
(1)
Se vogliamo che il proiettile colpisca un bersaglio posto in un punto P , di coordinate
x = a ed y = b, dovremo imporre che la traiettoria passi per il punto P determinando
di conseguenza i valori di q per cui questa condizione è soddisfatta. Dalla Eq. (1) si
ottiene quindi l’equazione di II grado in tgq:
(b + ga2/2v02) – a tgq + (ga2/2v02) tgq2 = 0
le cui soluzioni sono:
tgq = (v02/ga) ± [(v02/ga)2 – ( 1 + 2bv02/ga2)]0.5
(2)
affinchè le soluzioni siano reali, e quindi esista una traiettoria che passa per P, deve
essere:
(v02/ga)2 – ( 1 + 2bv02/ga2) ≥ 0
ovvero:
b £ v02/2g – (g/2v02) a2
(3)
Pertanto il bersaglio posto in P sarà colpito solo se le sue coordinate (a, b) soddisfano
questa disequazione, ovvero se P si trova nella regione di spazio delimitata dagli assi
x ed y e dalla parabola definita dall’Eq. (3) con il segno di uguale ( detta “parabola di
sicurezza”):
y £ v02/2g – (g/2v02) x2
Si noti che in queste condizioni è sempre possible colpire un bersaglio impostando
due diversi alzi: l’angolo più piccolo corrisponde ad una traiettoria più tesa, quello
maggiore corrisponde ad una traiettoria a “colombella” o da mortaio.
b) Fissate le coordinate del punto a = d e b = h , l’Eq. (3) fornisce immediatamente i
valori dei due angoli e risulta:
y (m)
q+ = 1.22 rad = 69.93°
q- = 0.426 rad = 24.40°
3500
3500
3000
3000
2500
2500
2000
2000
1500
1500
1000
ps
500
500
P
0
0
1000
2000
3000
4000
1000
5000
6000
0
7000
x (m)
Nella figura è riportata la parabola di sicurezza, indicata con ps, e le due possibili
traiettorie con cui è possible colpire un bersaglio posto in P ( intersezione delle due
parabole).
13) Nel piano del moto del corpo scegliamo un sistema di riferimento con l’asse x ,
posto a livello del terreno, diretto lungo l’orizzontale nel verso della componente
orizzontale della velocità dell’aereo, e con l’asse y verticale, diretto verso l’alto e
passante per il punto in cui avviene il distacco del bullone; si sceglie come istante
iniziale quello del suo distacco dall’aereo. Le componenti della velocità del
bullone all’istante iniziale, uguali a quelle della velocità dell’aereo, risultano v0x =
v0cosq e v0y = v0sinq ; le equazioni orarie per le componenti della velocità sono
quindi:
vx = v0x = v0cosq
vy = v0y – gt = v0sinq - gt
(1)
(2)
Per le coordinate del bullone al tempo t si ha:
x = v0xt = (v0cosq)t
y = h + v0yt - gt2/2 = h + (v0sinq)t - gt2/2
(3)
(4)
Eliminado t fra le Eq. (3-4) si ottiene l’equazione della traiettoria :
y = h + xtgq - gx2/2(v0cosq)2
(5)
a) La coordinata x* del punto di atterraggio la si ottiene immediatamente andando a
determinare in quale punto la traiettoria del bullone interseca il suolo ossia
ponendo nell’Eq. (5) y = 0 ; si ottiene così:
x* = (v02sinqcosq/g) + [(v02sinqcosq/g)2 – 2h(v0cosq)2/g ]0.5
e numericamente risulta x* = 2916.52 m
b) Il tempo di volo t* lo si ottiene dall’ Eq. (3) per x = x* e risulta:
t* = x*/(v0cosq)
t* = 24.2 s
c) La velocità del bullone al momento dell’impatto si ricava dalle Eq. (1-2) per t =
t*:
v*x = v0x = v0cosq
v*x = 120.28 m/s
v*y = v0y – gt* = v0sinq - gt*
v*y = -167.95 m/s
Il modulo della velocità risulta quindi dato da v* =( v*x2 + v*y2)0.5 = 206.6 m/s (653.7
Km/h).
d) Il bullone raggiungerà la massima quota all’istante t’ in cui la componente
verticale della sua velocità si annulla; ponendo quindi vy = 0 nell’Eq. (2) si ricava:
t’ = v0sinq/g
da cui, sostituendo nell’Eq. (4):
y’ = y(t’) = h + (v0sinq)2/2g
y’ = 1445.8 m
y(m)
e) Poichè la componente orizzontale della velocità rimane costante durante il moto,
il minimo valore di v lo si ottiene quando si annulla la componente verticale della
velocità, ossia al vertice della traiettoria, e risulta uguale a v0x = v0cosq ;
ugualmente la velocità è massima quando è massima la sua componente verticale,
ossia al momento dell’impatto col terreno, e risulta quindi uguale a v*.
Nel grafico di figura è riportata la traiettoria parabolica del bullone e la treiettoria
dell’aereo da cui si sgancia (linea tratteggiata )
1600
1600
1200
1200
800
800
400
400
0
0
500
1000
1500
2000
2500
0
3000
x(m)
14) Scegliamo un sistema di riferimento con l’origine O nel punto in cui si trova la
stazione radar, l’asse x orizzontale ed orientato nel verso di V e l’asse y verticale
orientato positivamente verso l’alto; scegliamo come istante iniziale quello in cui
il proiettile ha raggiunto l’apice della traiettoria. Le coordinate e le componenti
della velocità del proiettile all’istante iniziale sono quindi:
x0 = -Lcosq
y0 = Lsinq
v0x = V
v0y = 0
Le equazioni orarie per le coordinate del proiettile e per le componenti della velocità
sono quindi:
v0x = V
v0y = -gt
(1)
x = -Lcosq + Vt
y = Lsinq - gt2/2
(2)
a) Il priettile toccherà terra all’istante t = t* dato dall’equazione y = y(t*) = 0 ; dalla
Eq. (2) si ricava:
t* = (2Lsinq/g)0.5
t* = 16.6 s
per cui la coordinata del punto d’impatto risulta data da :
x* = -Lcosq + Vt*
x* = 2641 m
Il proiettile atterra quindi alla destra della stazione radar.
b) La traiettoria del proiettile è simmetrica rispetto alla linea verticale passante per il
vertice della parabola ( quindi esso impiega un tempo uguale a t* per arrivare dal
punto di sparo all’apice della traiettoria ) e la distanza lungo l’orizzontale del
vertice dal punto di sparo è uguale a Vt* (uguale alla distanza in orizzontale fra il
vertice ed il punto di atterraggio). La coordinata del cannone X risulta quindi:
X = -Lcosq - Vt*
X = -7318 m
c) La componente orizzontale della velocità del proiettile è costante; la componente
verticale, sempre per la simmetria della traiettoria, ha invece all’istante iniziale un
valore uguale ed opposto a quello che ha al momento dell’atterraggio. Pertanto si
ha:
v0x = V
v0y = gt* = (2Lgsinq)0.5
v0 = (V2 + 2Lgsinq)0.5
e quindi numericamente v = 341 m/s.
L’alzo b è dato immediatamente dalla relazione:
tgb = v0y/v0x = (2Lgsinq)0.5/V
b = 0.497 rad = 28.5°
2000
2000
y
y(m)
1500
1500
V
1000
1000
L
500
500
q
0
-1 104
-8000
-6000
-4000
-2000
x(m)
O
0
2000
0
4000
15) Scegliamo un sistema di riferimento con l’asse x orizzontale, a livello del suolo, e
l’asse y verticale, ascendente, e passante per il punto di lancio della freccetta;
scegliamo come istante iniziale quello di distacco della mela dal ramo.
a) Le equazioni orarie della mela sono:
yM = h - gt2/2
xM = d
(1)
mentre quelle della freccetta, scagliata al momento del distacco della mela, sono:
x = (v0cosq)t
y = l + (v0sinq)t - gt2/2
(2)
(3)
dove v0 è la velocità di lancio e q è l’angolo che essa forma con l’orizzontale.
La freccetta colpirà la mela se ad un determinato istante t* esse hanno le stesse
coordinate, quindi dovrà risultare:
xM = x
yM = y
Æ
Æ
d = (v0cosq)t*
h – gt*2/2 = l + (v0sinq)t* - gt*2/2
(4)
eliminando fra queste due equazioni il tempo t* si ottiene l’angolo q di lancio:
tgq = ( h – l )/d
q = 0.38 rad = 21.78°
Per colpire la mela si dovrà quindi mirare esattamente verso il punto di distacco dal
ramo.
b) Le precedenti equazioni determinano la quota a cui si colpisce la mela in
funzione della velocità v0 ; esiste quindi un valore minimo della velocità
per cui è possibile colpire il bersaglio prima che tocchi terra ed è fornito
dalla condizione:
yM = h – gt*2/2 > 0
per cui ricavando dall’Eq. (4) il valore di t* = d/(v0cosq) e sostituendo nella
disuguaglianza si ottiene:
v0 > (d/cosq)(g/2h)0.5
v0 > 6.88 m/s
In figura è riportata la traiettoria della freccetta per una velocità v0 = 10 m/s.
3.5
3.5
3
3
2.5
2.5
y (m)
h
2
2
1.5
1.5
v0
q
1
1
l
0.5
0.5
0
0
0
1
2
3
4
5
6
7
t (s)
c) Una volta che la velocità v0 sia stata fissata ad un determinato valore si
potrà colpire la mela ad una quota prefissata scegliendo opportunamente
l’istante di lancio t’ e la direzione di lancio b della freccetta.
Le equazioni orarie della mela rimangono inalterate, rispetto al caso a), mentre quelle
della freccetta, tenendo conto del ritardo t’ nel suo lancio, divengono:
x = (v0cosb)(t – t’)
y = l + (v0sinb)(t – t’) – g(t – t’)2/2
(4)
(5)
Dovendo la freccetta colpire la mela quando essa passa per il punto a quota l dovrà
risultare:
d = (v0cosb)(t – t’)
l = l + (v0sinb)(t – t’) – g(t – t’)2/2
con t dato dall’equazione:
yM = l = h – gt2/2
Risolvedo queste tre equazioni si ottiene:
sin2b = gd/v02
b = 0.325 rad =18.64°
t = [2(h – l)/g]0.5
t = 0.638 s
t’ = t – d/(v0cosb)
t’ = 52 ms
Nella figura seguente sono riportate le equazioni orarie per le quote della freccetta ( F
) e della mela ( M ).
3.5
3.5
3
3
y , yM ( m )
2.5
2.5
M
2
2
1.5
1.5
F
1
1
0.5
0.5
0
0
0
0.2
0.4
0.6
t (s)
0.8
1
16) In tutti i casi presi in considerazione nelle varie domande si ha a che fare con
moti circolari uniformi; quindi la velocità v e l’accelerazione centripeta a sono
dati, in modulo, dalle seguenti espressioni:
w = 2pn = 2p/T
v = wR
a = w2R = vw = v2/R
dove R è il raggio della circonferenza, T è il periodo associato col moto in esame e w
la frequenza angolare. Utilizzando i dati forniti per i vari casi si ha quindi:
a)
n = 10 Hz
T= 0.1 s
b)
T = 24 h = 86400 s
w = 62.8 rad/s
w = 7.27 10-5 rad/s
v = 31.4 m/s
a = 1972 m/s2 = 201 g
v = 463 m/s
a = 3.36 10 m/s = 3.43 10-3 g
-2
c)
T = 365 gg = 3.134 107 s
w = 1.99 10-7 rad/s
2
v = 2.98 104 m/s
a = 5.93 10 m/s2 = 6.04 10-4 g
-3
d) T = 2 1011 a.a. = 6.27 1018 s w = 1.00 10-18 rad/s
v = 3.096 10-7 m/s
a = 3.10 10-25 m/s2
17) Consideriamo un pianeta che si muove su un’orbita circolare di raggio R con una
velocità angolare w = 2p /T , dove T è il periodo di rivoluzione attorno al Sole;
l’accelerazione centripeta a cui è soggetto vale:
a = w2R = (2p/T)2R = (2p/R)2K = 4.23 1019/R2
dove si è sfruttata, nelle ultime espressioni la III Legge di Keplero.
Dato che questa relazione, che esprime l’accelerazione come il prodotto di una costante
per l’inverso del quadrato della distanza del pianeta dal Sole, vale identica qualunque sia
il pianeta considerato ne segue che essa è l’espressione di una stessa legge fisica. Questa
relazione sta alla base delle considerazioni che portarono Newton a formulare la Legge di
Gravitazione universale secondo cui due corpi puntiformi dotati di “massa” interagiscono
con una “forza” attrattiva inversamente proporzionale al quadrato della loro distanza e
diretta lungo la congiungente i due corpi. L’accelerazione con cui i pianeti ed i satelliti si
muovono sulle loro orbite e l’accelerazione di gravità sono il risultato di questa
interazione detta “gravitazionale”
18) a) In prossimità della superficie terrestre ogni corpo è soggetto all’accelerazione
di gravità g ( = 9.81 m/s2) diretta perpendicolarmente al suolo e quindi verso il
centro della terra. Questa accelerazione è il risultato dell’interazione
gravitazionale fra la Terra ed il corpo ed in base alla Legge di Gravitazione
universale essa è inversamente proporzionale al quadrato della distanza del corpo
dal centro della Terra, pari al raggio terrestre RT. Si ha quindi la relazione che
fissa il valore della costante di proporzionalità:
g = C/RT 2
b)
C = 3.98 1014 m3/s2
In base alla Legge di Gravitazione universale l’accelerazione centripeta a
cui è soggetta la Luna nel suo moto attorno alla terra è data dalla
relazione:
a = w2RTL = (2p/T)2RTL = C/RTL2 = gRT 2/RTL2
Dove T è il periodo di rivoluzione della Luna attorno alla Terra. Si ottiene allora da
questa relazione:
T = 2p(RTL3/C)0.5
T = 2.37 106 s = 27.43 gg
valore che, nei limiti delle approssimazioni fatte circa l’orbita della Luna, è in ottimo
accordo con il valore effettivo.
Queste valutazioni, effettuate in modo più raffinato e preciso, furono fatte dallo stesso
Newton per verificare la validità della Legge di Gravitazione universale.
c) Per un satellite artificiale che orbita attorno alla Terra periodo di rivoluzione T ( o
velocità angolare w) e raggio dell’orbita R , supposta circolare, sono strettamente
correlate dalla stessa relazione che abbiamo visto valere per la Luna ed abbiamo:
a = w2R = (2p/T)2R = C/R2 = gRT 2/R2
Nel caso di un satellite geostazionario la sua velocità angolare dovrà essere esattamente
uguale a quella della Terra di modo che la sua posizione rimanga fissa sopra la verticale,
o raggio, passante per un punto della superficie terrestre. Quindi risulta T = 24 h = 86400
s ed w = 7.27 10-5 rad/s da cui:
R = (C/w2)1/3
R = 4.22 107 m = 6.63 RT
19) a) Nell’ipotesi che il razzo si muova con velocità radiale costante v il tempo t*
impiegato a coprire la distanza Terra-Luna è dato dalla relazione:
t* = (RTL - RT)/v
b)
t* = 6.85 gg = 5.9184 105s
Indichiamo con r e RL i raggi che uniscono in centro della Terra al razzo
ed alla Luna rispettivamente e con q e qL gli angoli che essi fanno rispetto
ad uno stesso asse polare di riferimento, che scegliamo coincidente con la
v
RL
r
q
qL
congiungente Terra-Luna all’istante di lancio del razzo che scegliamo come
istante iniziale t = 0. Perchè il razzo colpisca la Luna, di cui si trascurano le
dimensioni, all’istante t* questi due raggi dovranno essere sovrapposti e
quindi q e q L dovranno essere uguali a meno di un multiplo intero di 2p.
Essendo all’istante t = 0 qL = 0 e q = q0 , le equazioni orarie per le
coordinate angolari del razzo e della Luna sono:
q = q0 + wTt
qL = wLt
dove w T è la velocità angolare del razzo , uguale a quella della Terra da cui viene
lanciato, e wL ( = w T/28 ) la velocità angolare della Luna. Per quanto detto al tempo t*
deve risultare
q = qL
Æ
q0 + wTt* = wLt* + 2pn
da cui:
q0 = ( wL - wT )t* + 2pn = - (27/28)wTt* + 2pn
numericamente risulta q0 = -0.60 2p = - 3.79 rad = - 217.3°. Per la coordinata angolare
della Luna al momento dell’impatto si ha invece: qL = wLt* ossia qL = 1.537 rad = 88.1°.
Le traiettorie della Luna (traccia circolare blu) e del razzo (spirale tratteggiata rossa )
sono riportate nel diagramma polare A della figura (v anche domanda e). Come si vede in
questo caso il razzo compirebbe, durante il suo avvicinamento alla Luna, circa 7 giri
attorno al’asse di rotazione terrestre. Nel diagramma polare B è riportato un
ingrandimento della parte iniziale del moto del razzo (traccia rossa)
c) La velocità vR del razzo quando raggiunge la Luna è la risultante della
componente radiale, pari a v, e della componente angolare pari a wTRTL ,
quindi si ha:
vR = [v2+ (wTRTL)2]0.5
d)
vR = 28 Km/s
In un punto qualsiasi della traiettoria a distanza r dal centro della Terra la
velocità vR del razzo è data da:
vR = [v2+ (wTr)2]0.5
Per l’accelerazione tangenziale risulta quindi dalla sua definizione, tenendo conto che
dr/dt = v :
at = dvR/dt = (dvR/dr)dr/dt = wT2vr/[v2+ (wTr)2]0.5
La massima accelerazione tangenziale la si ha per r = RTL per cui risulta numericamente
at = 4.64 10-2 m/s2 .
e) La traiettoria del razzo può essere calcolata immediatamente a partire
dalle equazioni orarie per le sue coordinate radiali ed angolari; si ha
infatti:
r = RT + vt
q = q0 + wTt
(1)
Eliminando il tempo fra queste due equazioni si ottiene:
r - RT = v(q - q0 )/wT
equazione che corrisponde ad un ramo di spirale di Archimede come mostrato nei
diagrammi polari delle figure.
f) In questo caso la velocità angolare w del razzo diminuisce con la distanza dal centro
della Terra, ossia del tempo, e precisamente risulta:
w = dq/dt = RT2wT/r2 = RT2wT/(RT + vt)2
(2)
dove nell’ultima espressione si è usata l’Eq. (1) per esprimere la distanza r in funzione
del tempo. L’Eq. (2) può essere integrata separando le variabili e si ottiene:
Ú
q
q0
t
dq '= Ú 0 dt' RT2wT
( RT + vt')
2
da cui:
q - q0 = wTt/(1 + vt/RT)
(3)
†
Imponendo come prima
che per t = t* la Luna e il razzo abbiano la stessa coordinata
angolare, a meno di multipli di 2p , si trova per l’angolo di lancio
q0 = wLt* - wTt*(RT/RTL)
e numericamente q0 = 0.823 rad = 47.1°. Anche in questo caso si ottiene l’equazione della
traiettoria eliminando il tempo fra l’Eq. (3) e la prima delle Eq. (1) e si ha:
RT(1 - RT/r ) = v(q - q0 )/wT
Nei grafici polari della figura la traiettoria del razzo è in questo caso rappresentata dal
tratto di spirale di colore verde; il raggio disegnato individual la direzione di lancio del
razzo, corrispondente a q0 = 47.1°.
A
B
90
4 105
120
60
90
3.5 105
4 104
3 105
60
3.5 104
2.5 105
30
3 104
2 105
30
2.5 104
1.5 105
2 104
5
1 10
1.5 104
5 104
0
0
210
330
240
r ( Km )
r ( Km )
120
1 104
5000
0
210
300
330
240
270
300
270
20) Il primo ciclista si muove di moto uniforme lungo l’anello del velodromo, quindi con
velocità angolare costante w1; velocità lineare v1 ed equazione oraria per la coordinata
angolare q1 sono dati da:
v1 = w1R
q1 = q10 + w1t = p/2 + w1t
(1)
Nello scrivere le Eq. (1) si è supposto di misurare l’angolo q a partire della linea di
partenza (e di arrivo) dei corridori e si è scelto come istante iniziale quello in cui parte
il secondo corridore , per cui q1(t = 0)= q10 = p/2. Durante il suo moto il ciclista 1
sarà soggetto unicamente all’ accelerazione centripeta ar1 = w12R.
Il secondo ciclista si muove con accelerazione angolare a costante ossia di moto
uniformemente accelerato. Con le scelte fatte per il riferimento angolare e l’istante
iniziale abbiamo le seguenti relazioni per l’equazioni orarie, la velocità lineare v2,
l’accelerazione tangenziale at2 e l’accelerazione centripeta ar2:
q2 = at2/2
w2 = at
1
2
q1
q2
O
v2 = w2R
at2 = aR
ar2 = w22R
a) Tenuto conto dell’angolo descritto dal raggio che individua la posizione del primo
ciclista nel tempo t* si ha:
w1 = [q1(t*) - q10]/t* = 19p/2t*
w1= 0.166 rad/s
v1 = 10.8 m/s = 38.8 Km/h
b) Dall’equazione oraria del secondo ciclista si ha per l’accelerazione angolare e
tangenziale:
a = 2q2(t*)/t*2 = 20p/t*2
a = 1.94 mrad/s2
at2= 0.126 m/s2
c) Dall’equazione oraria per la velocità del secondo ciclista si ha quando arriva al
traguardo:
w*2 = w2(t*) = at* = 20p/t*
w*2 = 0.349 rad/s
v*2 = 22.7 m/s = 81.7 km/h
d) Per il modulo delle accelerazioni dei due ciclisti sul traguardo si ha infine :
a*1 = ar1 = w12R
a*2 = [at22+ ar22]0.5 = [(aR)2+ (w*22R)2]0.5
a*1 = 1.79 m/s2
a*2 = 2.81 m/s2
21) In ogni punto della traiettoria è nota l’accelerazione totale agente sul proiettile che
risulta pari all’accelerazione di gravità g. Inoltre con i dati forniti è possibile
calcolare la traiettoria. che risulta essere una parabola data dell’Eq. (11-5), e
quindi in ogni punto è possibile calcolare la tangente alla traiettoria e la velocità.
Le componenti tangenziale at e normale a n dell’accelerazione possono quindi
essere calcolate proiettando g lungo la direzione tangente e normale alla taiettoria;
infine il raggio di curvatura r = v2/an può essere calcolato utilizzando
l’espressione generale dell’accelerazione normale.
a) La tangente alla traiettoria è individuata dalla direzione della velocità quindi
forma con l’orizzontale un angolo q . Le componenti dell’accelerazione e il raggio
di curvatura sono pertanto dati da:
an = 8.49 m/s2
at = - 4.9 m/s2
r = 7357 m
an = gcosq
at = -gsinq
r = v02/gcosq
La componente tangenziale dell’accelerazione può ovviamente essere calcolata
ricorrendo alla sua definizione at = dv/dt ottenendo identico risultato; si noti il segno
– nell’espressione di at che indica un decremento del modulo della velocità in questa
parte della traiettoria, ovvero un verso di at opposto a quello di v.
b) Nel punto più alto della traiettoria la tangente e quindi la velocità v’ sono
orizzontali e v’= v0cosq, ne segue pertanto immediatamente:
at = 0
an = 9.81 m/s2
r = 4778 m
an = g
r = (v0cosq)2/g
All’apice della traiettoria risulta at = 0 in conseguenza del fatto che il modulo della
velocità risulta minimo in questo punto.
c) Essendo la traiettoria simmetrica rispetto alla retta passante per il vertice della
parabola risulta immediatamente che le componenti dell’accelerazione ed il
raggio di curvatura sono uguali in modulo a quelle che si hanno nel punto di
lancio, calcolate in a). L’unica differenza riguarda il segno dell’accelerazione
tangenziale che in questo caso risulta positiva dato che il modulo della velocità, in
questa parte della traiettoria, aumenta (verso di at concorde con quello di v).
y
v’
v0
q
x
at
v’’
q
an
an
g
g
at
g
22) La velocità della barca, rispetto alla riva, è la somma vettoriale della velocità con
cui essa si muove rispetto all’acqua e della velocità di quest’ultima che
corrisponde alla velocità di trascinamento. In questo caso la denominazione di
“velocità di trascinamento” ha un significato immediato ed intuitivo in quanto la
barca immessa nell’acqua, senza velocità alcuna rispetto ad essa, viene trascinata
dalla corrente con velocità V. Volendo formalizzare il problema possiamo dire
che si ha un sistema di riferimento S solidale con la riva del fiume, un sistema di
riferimento mobile S’ , solidale con l’acqua del fiume, che trasla rispetto ad S con
velocità V, ed infine la barca che si muove relativamente ad S’ con velocità vB. La
velocità v della barca rispetto alla riva ( ossia nel sistema S ) è quindi data da:
v = V + vB
(1)
Questa relazione consente di rispondere a tutte le varie domande.
a) La velocità della barca v , data dalla Eq. (1) con v B = v 0 , è costante quindi la
barca si muove lungo la retta individuata dalla direzione di v a partire dalla
posizione iniziale A sulla riva; l’intersezione B di questa retta con la riva opposta
individua il punto di arrivo. Si ha pertanto per l’angolo q che v forma con le rive:
tgq = v0/V
q = 0.38 rad = 21.8°
Quindi indicando con H il punto opposto ad A sull’altra riva del fiume , la distanza D
= BH risulta data da:
D = L/tgq = LV/v0
D = 150 m
H
B
v0
v
L
q
V
A
b) Il tragitto spazialmente più breve è quello che va dal punto di partenza A al punto
H opposto ad esso sull’altra riva. Perchè la barca segua questo tragitto la velocità
v dovrà essere diretta lungo la retta passante per A ed H, quindi la sua
componente in direzione parallela alla riva dovrà essere nulla, ossia, in base
all’Eq. (1), la componente di vB parallela alla riva dovrà essere uguale ed opposta
aV:
V + vBcosq = 0
Æ
vB = - V/cosq
(2)
Il valore minimo di vB lo si ha in corrispondenza di un angolo che differisca da p di
una quantità infinitesima , quindi per vB = v* = V. E’ evidente che se non si è in grado
di imprimere alla barca una velocità superiore a V non si potrà mai contrastare
l’azione di trascinamento della corrente.
H
v
vB
q
V
A
c) L’Eq. (2) fornisce immediatamente il valore dell’angolo q richiesto ponendo vB =
3v* =3V :
cosq = -V/vB= -1/3
q = 1.91 rad = 109°
Tenuto conto che la barca si muove in direzione perpendicolare alle rive con una velocità
costante v = vBsinq = 3Vsinq si ha immediatamente per il tempo t’ , impiegato nella
traversata:
t’ = L/v = L/3Vsinq
t’ = 7.07 s
d) Il tempo T impiegato nella traversata è comunque dato da T = L/v’, con v’
componente della velocità della barca perpendicolare alle rive, quindi per
minimizzare T si deve rendere massimo v’ , ovvero dirigere la barca
perpendicolarmente alle rive di modo che v’ = 3V. Il tempo corrispondente risulta
quindi T = L/3V , ossia T = 6.66 s ; ovviamente la barca raggiungerà la riva
opposta in un punto a valle di H e precisamente in un punto distante da esso d =
VT , da cui d = 20 m.
23) Consideriamo un sistema di riferimento S , solidale col terreno, ed un sistema di
riferimento S’ solidale con l’auto su cui si trova il passeggero. Nel sistema S la
goccia ha velocità v con componente verticale pari a v0 , rivolta verso il basso, e
componente orizzontale , dovuta al vento, pari a V. Il sistema S’ , solidale con
l’auto, trasla rispetto ad S con velocità vA diretta lungo l’orizzontale, quindi, detta
v’ la velocità della goccia relativa ad S’ , si ha la relazione:
v = vA + v’
Da quanto detto risulta immediatamente che la componente verticale della velocità della
goccia è la stessa nei due sistemi di riferimento, mentre per le componenti orizzontali
abbiamo:
V = vA + v’
Æ
v’= V – vA
Avendo scelto un sistema di riferimento con l’asse orizzontale orientato positivamente
nel verso in cui spira il vento; l’equazione mostra che la velocità relativa v’ risulterà
comunque positiva se la macchina si muove nel verso opposto a quello in cui spira il
vento, mentre se si muove nello stesso verso sarà v’ > 0 ( < 0 ) se vA < V ( > V).
Nel caso in cui la macchina è ferma (vA = 0 ) v’ = V , l’angolo q 0 che la traccia della
goccia forma con la verticale discendente è dato dalla relazione:
tgq0 = v’/v0 = V/v0
(1)
Invece nel caso in cui la macchina sia in movimento l’angolo q è dato dalla relazione:
tgq = v’/v0 = (V – vA)/v0
(2)
Dalle equazioni (1-2) si ottiene per V e v0:
v0 = vA/( tgq0 - tgq)
V = v0tgq0
v0= 7.7 m/s
V = 4.44 m/s
24) Il problema può essere risolto nel modo più semplice considerando un sistema di
riferimento S’ solidale con la nave B, quindi che trasla con velocità costante vB
rispetto al sistema di riferimento S solidale con la banchina del porto. La velocità
dell’imbarcazione A rispetto ad S’ , v’A ,è data da:
vA = vB + v’A
Æ
v’A = vA – vB
Tenendo conto che le velocità delle navi sono uguali in modulo, un passeggero della
nave B vedrà avvicinarsi la nave A , lungo una retta corrispondente alla bisettrice
dell’angolo formato dalle rotte delle due navi, con una velocità di modulo v’A =
2vAcosf = 2vcosf con f = (p – b)/2 ( naturalmente lo stesso passeggero vede anche
avvicinarsi le banchine del porto con velocità vA ). Nel disegno la linea continua blu (
individuata dalla velocità relativa v’A) rappresenta la traiettoria della nave A come è
vista da un passeggero della nave B.
a) Tenuto conto che le rotte delle navi si intersecano in corrispondenza
dell’inboccatura del porto P (corrispondente anche alla posizione
dell’imboccatura del porto in S’ all’istante iniziale ) e che la minima distanza d
fra le due navi corrisponde alla distanza BH della nave B dalla rota seguita da A
nel sistema di riferimento S’ si ha immediatamente dal triangolo PBH:
d = Dsinf
b)
d = 259 m
Quando la nave A raggiunge , al tempo t*, la minima distanza da B si trova, in
S’, ad una distanza dalla sua posizione iniziale pari alla lunghezza l d e l
segmento PH e risulta l = Dcosf. Muovendosi con velocità costante v’A lungo la
sua rotta, il tempo t* risulta dato da:
t* = l/v’A = D/2v
A
t* = 50 s
P
f f
D
vA
P’
v’A
vB
B
d
H
c)
Le distanze delle due navi dall’imboccatura del porto P al tempo t* risultano
date immediatamente dalle relazioni:
dA = vt* = D/2
dB = D - vt* = D/2
dA = 500 m
dB = 500 m
25) a) Scelto il sistema S solidale con la tromba dell’ascensore, possiamo risolvere il
problema scrivendo le equazioni di moto per il bullone ed il pavimento
dell’ascensore. Il bullone cade, partendo da fermo dato che la velocità
dell’ascensore nell’ istante di distacco è nulla, sotto l’azione della accelerazione di
gravità. Pertanto scelto un asse y verticale, orientato positivamente verso l’alto, e
l’origine O in corrispondenza della quota del pavimento dell’ascensore all’istante
iniziale, le equazioni orarie per la coordinata e la velocità del bullone sono date
da:
yB = h – gt2/2
vB = -gt
(1)
Il pavimento dell’ascensore nell’istante in cui il bullone si stacca inizia a muoversi
verso l’alto, partendo da fermo, con accelerazione costante A. Le sue equazioni orarie
sono pertanto:
yP = At2/2
vP = At
(2)
Nell’istante t = t* in cui il bullone urta il pavimento dell’ascensore le loro coordinate
saranno uguali, pertanto si ha l’equazione:
yB = yP
Æ
h – gt*2/2 = At*2/2
che fornisce per l’istante cercato:
t* = [2h/(g + A)]0.5
t* = 0.61 s
Per le velocità del bullone e del pavimento all’istante dell’urto si ha invece:
v*B = -gt*
v*P = At*
vB = -5.98 m/s
vP = 1.22 m/s
La velocità del bullone rispetto al pavimento v’* è quindi , nell’istante considerato:
v’* = v*B – v*P = - (g + A)t* = - [2h(g + A)]0.5
y
v’ = -7.2 m/s
y’
S
S’
A
g
g
a’
-A
b) Il sistema S’ solidale con la gabina dell’ascensore è quello di un passeggero del
medesimo che vede staccarsi, con velocità nulla, il bullone dal soffitto. Il sistema
S’, che scegliamo con un asse verticale y’, orientato verso l’alto, e con l’origine
O’ sul pavimento dell’ascensore , trasla rispetto ad S con accelerazione A e
velocità istantanea vP , rivolte verso l’alto. Indicate con a’ e con v’ l’accelerazione
e la velocità relativa del bullone in S’ , si hanno le relazioni fra le accelerazioni e
le velocità in S ed S’ :
vB = vP + v’
- g = A + a’
Quindi il bullone si muove in S’ di moto rettilineo uniformemente accelerato sotto
l’azione di una accelerazione a’ = - (g + A). Di conseguenza le sue equazioni orarie
saranno in S’:
y’B = h + at2/2 = h – (g + A)t2/2
v’ = a’t = -(g + A)t
Imponendo la condizione y’B = 0 nella prima equazione si determina l’istante t* di
impatto col pavimento e conseguentemente la velocità, con risultati ovviamente
uguali a quelli trovati al punto a).
y
y’
S
S’
-A*
g
a’
A*
g
c) Nel caso che l’ascensore si muova verso il basso con accelerazione A*= -A le
equazioni scritte risultano uguali con l’eccezione del segno dell’accelerazione.
Cambiando nelle precedenti equazioni A con – A si ottiene per il tempo di impatto
t’ = [2h/(g - A)]0.5
t’ = 0.75 s
v” = - (g - A)t* = - [2h(g - A)]0.5
v” = - 5.86 m/s
e per la velocità
Come si vede il tempo di caduta risulta più lungo e la velocità di impatto più piccola
rispetto ai valori determinati per il caso precedente.
26) Nel sistema di riferimento S solidale con il terreno il corpo si muove sotto
l’azione dell’accelerazione di gravità g e, essendo la sua velocità iniziale nulla, si
muove lungo la verticale. Il sistema di riferimento S’ trasla lungo l’orizzontale,
rispetto ad S. Indichiamo con v’ e a’ la velocità e l’accelerazione del corpo nel
sistema S’ (velocità ed accelerazione relative) e con V e A la velocità istantanea
di traslazione e l’accelerazione di S’ rispetto ad S (velocità ed accelerazione di
trascinamento). Le accelerazioni a cui è soggetto il corpo e le velocità nei due
sistemi di riferimento sono legate fra loro dalle relazioni:
g = a’ + A
v = v’ + V
(1)
y
S
h
g
v0
A
x
y’
S’
- v0
-A
x’
g
a’
Per i due sistemi di riferimento si scelgono: gli assi y ed y’ diretti lungo la verticale,
orientati positivamente verso l’alto e coincidenti all’istante iniziale con la verticale
passante per il corpo; gli assi x e x’ orizzontali e a livello del suolo. (N.B. Nelle figure
gli assi risultano traslati per necessità di chiarezza grafica). L’istante iniziale t = 0
viene fissato al momento del distacco del corpo e si suppone l’accelerazione A e la
velocità V ( orizzontali) dirette nel verso opposto a quello di orientazione degli assi x
e x’.
L’equazioni (1) , proiettate lungo gli assi coordinati forniscono per le componenti
dell’accelerazione a’ e della velocità iniziale v0’ = v’(t = 0):
a’x = A
v’0x = v0
a’y = -g
v’0y = 0
Il moto del corpo (se A ≠ 0) sarà pertanto un moto uniformemente accelerato lungo
entrambi gli assi x’ e y’. Essendo x’( t = 0) = 0 e y’( t = 0) = h l’equazioni di moto
assumono la forma generale:
x’ = v0t + At2/2
y’ = h - gt2/2
Queste equazioni esprimono la traiettoria del corpo in forma parametrica; eliminando
fra di esse il tempo si ottiene l’equazione della traiettoria:
[x’ + (A/g)(y’- h)]2 = 2v02(h - y’)/g
(2)
che corrisponde in generale ad un arco di parabola.
a) Nel caso in cui A = 0 l’Eq. (2) diviene:
y’ = h – gx’2/2v02
che corrisponde esattamente ad una parabola con il vertice nel punto di distacco del
corpo.
b) Nel caso in cui v0= 0 l’Eq. (2) degenera nell’equazione della retta:
y’ = h – (g/A)x’
c) Come già detto in precedenza la traiettoria è in questo caso un arco di parabola.
Le traiettorie per i vari casi considerati sono riportate in figura: (v0 = 0, A = 2 m/s2)
linea tratteggiata verde, (v0 = 15 m/s, A = 0 m/s2) traccia rossa, (v0 = 15 m/s, A = 5
m/s2) traccia tratteggiata nera; inoltre è riportato anche il caso (v0 = 15 m/s, A = 2
m/s2) traccia blu.
A conclusione dell’esercizio è utile ribadire che nel sistema S’ , se A≠ 0, il corpo è
soggetto ad un’ accelerazione a’ = ( g – A ) ossia ad una accelerazione costante di
modulo a’ = (g2 + A2)0.5 diretta lungo la direzione della risultante di (g – A) ossia
lungo una retta di coefficiente angolare –(g/A). Sono quindi facilmente prevedibili ed
interpretabili i risultati trovati, in particolare quello del punto b), dato che il moto del
corpo è quello conseguente all’azione di un’accelerazione costante a’ che agisce
lungo una direzione obliqua rispetto alla verticale.
0
-0.5
y'(m)
-1
-1.5
a=5
-2
a=0
-2.5
v0 = 0
a=2
-3
0
0.5
1
1.5
2
x' ( m )
2.5
3
3.5
4
27) Nel sistema di riferimento S, solidale con il terreno, la traiettoria del corpo P è
nota; scelto l’asse x orizzontale e coincidente con la traiettoria del corpo, l’asse z
verticale e coincidente con l’asse di rotazione della giostra e scegliendo come
istante iniziale quello di passaggio del corpo per l’origine O ( posta sull’asse di
rotazione) si ha:
x = vt
y=0
z=0
y
S’
x’
y’
S
v
q
O
x
P
Il sistema S’, solidale con la giostra, ruota rispetto ad S con velocità angolare costante
w ( con i dati del problema w = 0.105 rad/s ); in questo caso la determinazione della
traiettoria del corpo nel sistema S’ è ottenuta applicando semplicemente la relazione
di trasformazione delle coordinate fra sistemi ruotanti. Per il sistema S’ si sceglie
l’asse z’ verticale e coincidente con l’asse di rotazione della giostra e l’asse x’
orizzontale e coincidente con l’ asse x all’istante iniziale. All’istante t , quando l’asse
x’ è ruotato di un’angolo q = wt rispetto alla posizione iniziale ( coincidente con
l’asse x ) , un punto P , di coordinate in S ( x, y = 0, z = 0) (rappresentativo della
posizione del corpo) , ha in S’ coordinate:
x’ = xcosq = xcoswt
y’ = - xsinq = - xsinwt
z’ = 0
tenuto conto che x = vt l’equazioni orarie che descrivono il moto del corpo nel
sistema della giostra sono:
x’ = vtcoswt
y’ = - vtsinwt
L’equazione della traiettoria può anche essere riscritta in forma più compatta in
termini della distanza del corpo da O’≡ O , data da r’ = vt , e dell’angolo polare, q’ =
-wt , che il segmento O’P ≡ r’ forma rispetto all’asse x’; eliminando fra le espressioni
di r’ e q’ il tempo si ottiene:
r’ = - (v/w)q
Questa equazione rappresenta una spirale di Archimede, e pertanto l’osservatore sulla
giostra vedrà il corpo muoversi lungo una curva di questo tipo il cui andamento è
riportato nel diagramma polare di figura.
90
120
10
60
8
6
30
4
r' ( m )
2
0
0
210
330
240
300
270
(N.B. - L’osservatore in S , solidale col terreno, vede un corpo che si muove con
velocità costante e quindi non soggetto ad accelerazione; l’osservatore sulla giostra
vede invece un corpo che si muove lungo una spirale e quindi necessariamente
soggetto ad una accelerazione non nulla. Come sarà detto a suo tempo, considerando
la dinamica dei corpi, questa diversità implica una sostanziale differenza fra i due
sistemi di riferimento. )
28) La velocità di un qualsiasi punto P del disco può essere espressa a partire dalla
velocità angolare w e dalla velocità di traslazione di un punto di riferimento
qualsiasi del disco per mezzo della relazione fondamentale della cinematica dei
corpi rigidi. Scegliendo in essa come punto di riferimento, con cui caratterizzare il
moto di traslazione del corpo, il centro O si ha:
vP = v0 + w Ÿ (P – O) = v0 + w Ÿ r
(1)
Scelto un sistema di riferimento con l’asse x orizzontale, orientato nel verso di v0,
l’asse y verticale ascendente, e l’asse z fissato di conseguenza si ha:
v0 = iv0
w = wk
r = r[isinq + jcosq]
dove i , j , k sono i versori lungo i tre assi x,y,z e q è l’angolo che il raggio r = OP
forma ad un certo istante con l’asse y. Le componenti della velocità di P sono quindi:
vPx = v0 - wrcosq
vPy= wrsinq
(2)
y
q P
O r
vP
d
x
C
(N.B.- Nello scrivere l’espressioni (2) si è fatto riferimento ad una terna “destrorsa”
nella quale il verso positivo di rotazione, e di misurazione degli angoli, è quello
antiorario).
a) Supponendo che il disco ruoti con velocità angolare costante, in modulo pari ad W
, in verso orario , per cui w = -W , si ha per i vari punti del bordo del disco ( r =
R):
(A ; q = 0 )
vAx = v0 + WR
vAy= 0
(B ; q = p/2 )
vBx = v0
vBy= -WR
(C ; q = p )
vCx = v0 - WR
vCy= 0
(D ; q = 3p/2 )
vDx = v0
vDy= WR
A
vA
vR
vD
B
D
v0
C
vB
vC
Come si vede dall’espressione (1) la velocità in ogni punto è la somma vettoriale
della velocità di traslazione e della velocità di rotazione attorno ad O.
( N.B. - Particolare importanza ha la velocità del punto C di contatto fra la ruota ed
il terreno. Come si vede dalla sua espressione vC > 0 se v0 > W R , ossia se la
componente traslazionale della velocità è maggiore di quella rotazionale; per
esempio al limite W = 0 (rotazione bloccata) il disco “struscia” sul piano come
accade quando si bloccano le ruote di una macchina a causa di una frenata troppo
brusca. Si ha invece vC < 0 se v0 < W R , ossia se la componente rotazionale della
velocità di C prevale su quella traslazionale; al limite v0 = 0 (traslazione del mozzo
della ruota bloccata) la ruota “slitta” sul terreno come accade quando la ruota di
una macchina rimane insabbiata.)
b) Il particolare moto che si realizza quando la ruota trasla con velocità v0 del centro
O e contemporaneamente ruota in verso orario con velocità W = v0/R riveste
notevole importanza e viene detto “moto di puro rotolamento” ( si dice anche che il
disco “rotola senza strisciare” ); in queste condizioni si vede subito che per quanto
riguarda il punto di contatto col terreno si ha:
(C ; q = p )
vC = v0 - WR = 0
(3)
Quindi nel moto di puro rotolamento la velocità del punto C del disco che ad un
determinato istante si trova a contatto col terreno deve essere nulla. Questa
condizione, espressa dall’equazione (3), costituisce la “condizione di puro
rotolamento” e determina un preciso legame fra la velocità del centro del disco e la
sua velocità angolare. Per questo tipo di moto la relazione (3) ( indipendentemente da
come è stata ricavata) vale in qualsiasi istante facendo ovviamente riferimento alle
velocità istantanee, quindi non solo se le velocità sono costanti. Questa relazione
costituisce una condizione necessaria e sufficiente per la sussistenza di un moto di
puro rotolamento: la condizione vC = 0 vale necessariamente se il moto è di questo
tipo e viceversa è sufficiente verificare che vC = 0 per asserire che il moto è di puro
rotolamento.
In queste condizioni per il punto A , diametralmente opposto a C, si ha:
(A ; q = 0 )
vA = v0 + WR = 2WR = 2v0
A
vA
vD
B
D
C
vC = 0
vB
c) Per il modulo di un generico punto P si ha immediatamente dalle Eq. (2), tenuto
conto della condizione di puro rotolamento v0 = WR:
vP = [vPx2 + vPy2]0.5 = [v0 2 + (Wr)2 + 2v0Wrcosq] 0.5 = W[R 2 + r2 + 2Rrcosq] 0.5 = Wd
dove d = PC rappresenta la distanza del punto P dal punto C di contatto col terreno.
Il vettore (P – C) = d risulta dato da:
d = irsinq + j(R + rcosq)
Tenuto conto delle Eq. (2) si verifica subito che il prodotto scalare d•vP = 0 per cui i
due vettori risultano perpendicolari.
In conclusione quindi, essendo I) la velocità di C nulla , II) la velocità di un punto
qualsiasi P del disco diretta perpendicolarmente alla congiungente P con C e III) di
modulo Wd , pari al prodotto della velocità angolare per la distanza di P da C , si può
affermare che il moto di puro rotolamento corrisponde, istante per istante, ad un moto
di pura rotazione attorno a C , che per qusto viene detto “centro di istantanea
rotazione”.
A questa conclusione si poteva anche arrivare immediatamente dalla relazione
fondamentale della cinematica dei corpi rigidi scegliendo come punto di riferimento
del corpo rigido C, infatti si ha:
vP = vC + w Ÿ (P – C) = w Ÿ d
w = -Wk
(4)
Riassumendo un moto di puro rotolamento può essere descritto in modo conveniente
e del tutto equivalente o come il risultato di un moto di traslazione del suo centro O
con velocità v0 più una rotazione attorno ad esso con velocità angolare W = v0/R (
moto roto-traslatorio) oppure come una semplice rotazione attorno a C con la stessa
velocità angolare W.
29) Consideriamo il moto del punto P del bordo del disco che all’istante iniziale si
trova nel punto più alto della circonferenza. Scegliamo un sistema di riferimento con
l’asse y verticale ascendente e passante per la posizione iniziale di P e l’asse x
orizzontale, giacente nel piano su cui rotola il disco, e orientato nel verso della
velocità del centro O; di conseguenza P all’istante t = 0 ha coordinate ( x = 0 , y = 2R
). La velocità del punto P ad un qualsiasi istante è data dalla relazione fondamentale
della cinematica dei corpi rigidi
vP = v0 + w Ÿ (P – O) = v0 + w Ÿ r
(1)
che fornisce per le componenti della velocità:
vPx = v0 + WRcosq = WR(1 + cosWt)
vPy= - WRsinq = -WRsinWt (2)
dove q = Wt è l’angolo che il raggio r forma con l’asse y all’istante t e si è tenuto
conto della condizione di puro rotolamento v0 = Wt W = |w|.
y
P
P’
q
O xO
O’
x
a) La traiettoria di P può essere determinata integrando direttamente le Eq. (2)
rispetto al tempo, oppure , in modo del tutto equivalente e senza eseguire gli
integrali, tenendo conto che il moto di puro rotolamento è il risultato della
composizione di un moto di traslazione lungo l’orizzontale con velocità costante
v0 e di un moto di rotazione attorno ad O con velocità angolare costante W. Di
conseguenza all’istante t il centro O del disco è traslato di una quantità xO = v0t =
W Rt , mentre il raggio r è ruotato di un angolo q = W t. Con semplici
considerazioni geometriche si ha allora per le coordinate del punto P.
x = RWt + Rsin Wt
y = R + RcosWt
Queste relazioni esprimono in forma parametrica l’equazione di una “cicloide” che è
appunto la traiettoria di un punto del bordo di un disco che rotola senza strisciare.
b) In un sistema di riferimento S’, solidale col centro del disco, che trasla con
velocità costante v0 il punto P descrive un moto circolare uniforme con velocità
angolare W. L’accelerazione a cui è soggetto P in S’ è quindi l’accelerazione
centripeta ar = W 2R diretta da P verso O ; dato che l’accelerazione di
trascinamento di S’ rispetto ad un sistema S, solidale col terreno, è nulla (v0 = cost
fi aT= 0) ne risulta che in S l’accelerazione di P è ancora uguale
all’accelerazione centripeta.
c) Per individuare le componenti tangenziale e normale della traiettoria è
innanzitutto necessario determinare la direzione della velocità in un punto
qualsiasi. Questo può essere fatto nel modo più semplice ricordando che il moto
di puro rotolamento può essere interpretato come una pura rotazione, con velocità
angolare W, attorno al punto di contatto col terreno C; di conseguenza la velocità
è perpendicolare al segmento CP e l’angolo OPC risulta uguale a q/2 dove q è
sempre l’angolo che il raggio r forma con l’asse y.
2.5
2
y (m )
1.5
1
P
0.5
2
0
3
1
0
0
0.5
1
1.5
2
2.5
x (m)
Le componenti tangenziale e normale dell’accelerazione sono quindi:
an = arcos(q/2) = W2Rcos(Wt/2)
(3)
at = Sarsin(q/2) = SW2Rsin(Wt/2)
( S = – 1 0 < (q –2np) < p fase discendente, + 1 p < (q –2np) < 2p fase ascendente )
1
0.8
y(m)
0.6
at
P
0.4
v
q
O
a
an
0.2
C
0
0
0.2
0.4
0.6
0.8
1
x (m)
Nel punto più alto della traiettoria (q = 2np) l’accelerazione tangenziale è nulla, in
accordo col fatto che il modulo della velocità è massimo, mentre l’accelerazione normale
vale in modulo W2R ed è diretta lungo la verticale verso il basso. Nel punto più basso
della traiettoria (q = (2n + 1)p) la componente normale è nulla mentre l’accelerazione
tangenziale vale in modulo W2R ed è diretta lungo la verticale verso l’alto.
( Nota - Per calcolare la componente tangenziale dell’accelerazione si poteva anche
ricorrere alla sua definizione. Tenuto conto che il modulo della velocità è v = WR(PC) =
2WR|cos(Wt/2)| si ha at = dv/dt = 2WRd|cos(Wt/2)|/dt ).
d) Il raggio di curvatura in un punto qualsiasi della traiettoria può essere ottenuto
dall’espressione dell’accelerazione normale e risulta r = v2/an. Tenuto conto dell’Eq. (3)
si ha:
r = 4R|cos(Wt/2)| = 2(PC) = 2PC
( N.B. – Come si vede r risulta doppio della distanza del punto P dal centro di istantanea
rotazione C; in generale quindi per un punto qualsiasi il raggio di curvatura della
traiettoria sarà diverso dal raggio della circonferenza su cui esso si muove ad
determinato istante.)
30) a) Nel caso in cui l’estremo B sia incernierato al manicotto M il sistema
ha un solo grado di libertà; per individuare la configurazione del sistema si può
scegliere, in modo conveniente, l’angolo f , misurato positivamente in verso
antiorario, che il raggio OP forma con la guida in cui scorre il manicotto.
y
P
x
f
O
B≡M
La velocità e l’accelerazione di un qualsiasi punto del sistema potranno quindi essere
espresse in termini della velocità angolare w e dell’accelerazione angolare a del
disco, che costituiscono le uniche variabili cinematiche essenziali. Le relazioni fra le
varie grandezze cinematiche e a ed w possono essere ottenute a partire dalle relazioni
geometriche che tengano ovviamente conto dei vincoli; scelto un sistema di
riferimento con l’origine nel centro O del disco e l’asse x coincidente con la guida
per i punti P e B ≡ M si ha:
xP = Rcosf
xB = 2Rcosf
yP = Rsinf
yB = 0
(1)
(2)
Le rispettive componenti della velocità possono essere ottenute immediatamente dalle
precedenti relazioni geometriche per derivazione:
vPx = - wRsinf
vBx = - 2wRsinf
vPy = wRcosf
vBy = 0
(3)
(4)
Analogamente per l’accelerazione derivando le Eq. (3-4) si ottiene:
aPx = - aRsinf - w2Rcosf
aBx = - 2aRsinf - 2w2Rcosf
aPy = aRcosf - w2Rsinf
aBy = 0
Per quanto riguarda il punto P quelle adesso calcolate sono le componenti lungo gli assi x
ed y dell’accelerazione: se , come accade in molti casi , si vogliono le componenti radiale
e tangenziale, tenendo conto che P si muove su una circonferenza di raggio R con
velocità v = wR , dalle definizioni risulta:
aPr = - w2R
aPt = aR
b)Nel caso particolare in cui il disco ruota con velocità angolare costante w, la
velocità ed l’accelerazione sono immediatamente ricavate dalle precedenti espressioni
del punto a) ponendo a = 0 e f = wt. Le espressioni della velocità sono identiche a
quelle delle Eq. (3) e (4) e si ha quindi:
vBx = - 2wRsinwt
vBy = 0
Per l’accelerazione si ottiene invece:
aBx = - 2w2Rcoswt = - w2xB
aBy = 0
Come si vede da queste espressioni il punto B descrive lungo la guida un moto armonico
di ampiezza 2R.
d) Nel caso in cui l’estremo B dell’asta non sia più vincolato a scorrere lungo l’asta
il sistema ha due gradi di libertà: per individuare completamente la configurazione del
sistema è necessaria oltre all’angolo f un’altra coordinata , che può per esempio
essere l’angolo q che la sbarra PB forma con l’asse x , misurato positivamente in
senso antiorario.
y
P
B
q
f
O
x
Per il punto P non cambiano rispetto al caso precedente le relazioni geometriche e di
conseguenza la sua velocità e la sua accelerazione sono identiche a quelle
precedentemente calcolate. Per il punto B si ha invece:
xB = Rcosf - Rcosq
yB = Rsinf - Rsinq
Derivando rispetto al tempo queste espressioni si ricava per le componenti della velocità:
vBx = - wRsinf + w*Rsinq
vBy = wRcosf - w*Rcosq
dove w* = dq/dt. Analogamente per l’accelerazione, posto a* = dw*/dt, si ha:
aPx = - aRsinf - w2Rcosf + a*Rsinq - w*2Rcosq
aPy = aRcosf - w2Rsinf - a*Rcosq + w*2Rsinq
31) Il sistema in oggetto ha un solo grado di libertà, infatti una volta fissata la posizione
del punto B risulta automaticamente fissata la posizione di P essendo fissata la lunghezza
L della funicella PAB. La configurazione del sistema può convenientemente essere
individuata tramite l’angolo f , misurato positivamente in verso orario, che la funicella
OB forma rispetto ad una retta orizzontale. Scegliamo un sistema di riferimento con
l’origine in O, l’asse x coincidente con la direzione ed il verso da O ad A e l’asse y
verticale ascendente.
y
O
A
f
B
P
x
Le coordinate dei punti B e P sono quindi:
xP = l
xB = lcosf
yP = -[L - 2lsin(f/2)]
yB = - lsinf
(1)
(2)
Posto w = df/dt e a = dw/dt si ha per derivazioni successive dell’Eq. (1-2):
vPx = 0
vBx = - wlsinf
vPy = wlcos(f/2)
vBy = - wlcosf
aPy = aRcos(f/2) - (w2R/2)sin(f/2)
aBy = - alcosf + w2lsinf
aPx = 0
aBx = - alsinf - w2lcosf
Come si vede è quindi possible esprimere velocità ed accelerazione di P e B unicamente
in termini della velocità angolare w e dell’accelerazione angolare a.
32) a) Nel caso in cui la rotazione del cilindro sia bloccata il sistema
costituisce un’unico corpo rigido ed esso ha un solo grado di libertà
muovendosi l’estremo A a contatto con la parete verticale e il cilindro sul
piano orizzontale. La configurazione del sistema può essere individuata
convenientemente per esempio mediante l’angolo f , misurato positivamente
in verso antiorario, che la sbarra OA forma con la verticale discendente.
y
A
f
O
x
Il sistema , come ogni corpo rigido, compirà un moto roto-traslatorio, ma
avendo un solo grado di libertà una soltanto sarà la varibile cinematica
indipendente e quindi velocità di traslazione e velocità angolare risulteranno
legate fra di loro. Il legame fra la velocità angolare w = df/dt , l’accelerazione
angolare a = dw/dt , la velocità e l’accelerazione dei vari punti e ricavato a
partire dalle relazioni geometriche. Scelto un sistema di riferimento con l’asse
x orizzontale, orientato positivamente nel verso del moto di O, e l’asse y ,
orientato positivamente verso l’alto, nel piano verticale su cui si muove A ,
per i punti A ed O in questo caso si ha:
xA = 0
xO = 4Rsinf
yA = R + 4Rcosf
yO = R
(1)
(2)
Velocità ed accelerazioni di A ed O sono ottenute per derivazione successive,
rispetto al tempo, delle relazioni (1-2).
vAx = 0
vOx = 4Rwcosf
vAy = - 4Rwsinf
vOy = 0
aAx = 0
aOx = 4Racosf - 4Rw2sinf
aAy = - 4Rasinf - 4Rw2cosf
aOy = 0
b) In questo caso il sistema, rispetto al caso precedente, ha un grado di libertà
addizionale dato dalla rotazione del cilindro attorno al proprio asse e di conseguenza
dovremo considerare anche la relativa velocità angolare W. Per quanto riguarda i
punti A ed O le relazioni geometriche (1-2) non cambiano , quindi saranno identiche
le espressioni della velocità e dell’accelerazione. Per quanto riguarda W la condizione
di puro rotolamento comporta un legame fra essa e la velocita del centro O e
precisamente risulta:
W = vOx/R = 4wcosf
e per l’accelerazione angolare A = dW /dt :
A = aOx/R = 4acosf - 4w2sinf
Nel caso di puro rotolamento quindi anche la velocità angolare W del disco è
esprimibile in termini di w e analogamente per l’accelerazione A.
c) Nel caso in cui il cilindro rotoli e strisci non esiste più alcun legame fra la sua
velocità angolare W e le altre variabili cinematiche (in particolare con la velocità del
centro O ) per cui essa è del tutto indipendente. Le relazioni (1-2) rimangono invece
inalterate.
d) Nel caso in cui l’estremo A della sbarra non sia più appoggiato alla parete
verticale per individuare completamente la posizione e la configurazione del
sistema, avendo bloccato la rotazione del cilindro ( caso a)), non è più sufficiente
l’angolo f .
Oltre a questo si dovrà per esempio assegnare anche una coordinata di un punto del
sistema, per esempio l’ascissa di O: quindi il sistema ha due gradi di libertà, le
coordinate indipendenti sono adesso f e xO e di conseguenza risultano variabili
cinematiche indipendenti w e vOx. Per quanto riguarda il punto A si ha adesso
xA = xO – 4Rsinf
yA = R + 4Rcosf
y
A
f
O
x
Da cui per velocità ed accelerazione si ottiene
vAx = vOx - 4Rwcosf
vAy = - 4Rwsinf
aAx = aOx - 4Racosf - 4Rw2sinf
aAy = - 4Rasinf - 4Rw2cosf
Nel caso di puro rotolamento del cilindro ( caso b)) la sua velocità angolare W è
legata alla velocità di traslazione del centro O dalla relazione W = vOx/R e le
espressioni della velocità ed accelerazione di A rimangono inalterate. Nel caso che il
cilindro rotoli e strisci invece la relazione ora scritta non è più valida e W risulta
essere una variabile cinematica indipendente.