Funzioni
Definizione: il dominio naturale (o campo di esistenza) di una funzione y = f(x) è l’insieme più
ampio di valori reali che si possono assegnare alla variabile indipendente x affinché esista il
corrispondente valore y.
Di solito non viene fornito ma si ricava dalla legge della funzione.
Esempi:
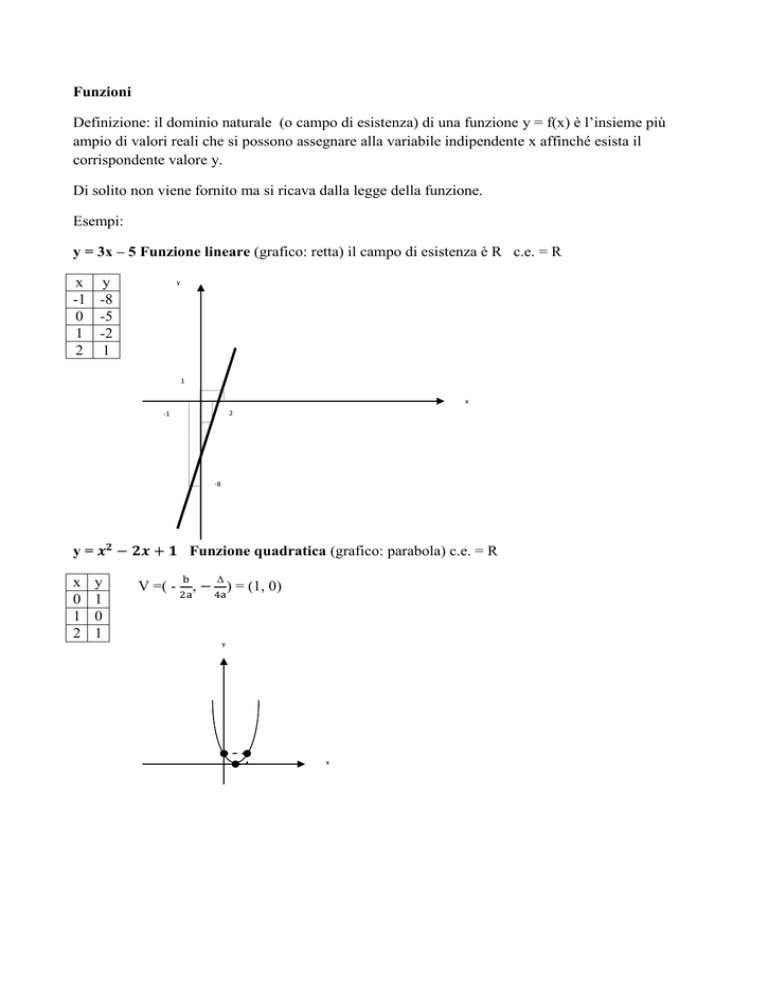
y = 3x – 5 Funzione lineare (grafico: retta) il campo di esistenza è R c.e. = R
x y
-1 -8
0 -5
1 -2
2 1
y
1
x
2
-1
-8
y=
x
0
1
2
Funzione quadratica (grafico: parabola) c.e. = R
y
1
0
1
V =( -
,
) = (1, 0)
y
x
y=
funzione fratta (grafico iperbole) c.e = x 0
x
y
-2 -1/2
-1
-1
1
1
2
1/2
-1/2 -2
1/2
2
(- , 0) U ( 0, + )
y
x
Il grafico della funzione si avvicina sempre di più all’asse y senza toccarlo mai, si dice allora che
l’asse y è un asintoto verticale per la funzione di equazione x=0
y=
c.e.
x
2
6
11
18
Funzione irrazionale
x-2 0
x 2
y
0
2
3
4
2
[2, + )
y
x
y=
x y
-7 -2
0 -1
1 0
9 2
Funzione irrazionale c.e.: R
y
x
Intersezioni di una funzione con gli assi cartesiani
Si ottengono mettendo a sistema l’equazione della funzione con le equazioni dei due assi cartesiani.
Intersezioni asse x
y = f (x)
y=0
Intersezioni asse y
y = f (x)
x=0
La soluzione del primo sistema cioè i valori a € R tale che f(a) = 0 si dicono zeri della funzione
Esempi:
y = 4x- 2
Intersezioni asse x
y = 4x-2
y=0
Intersezione asse y
y = 4x-2
x=0
y=0
4x-2 =0
y=0
4x = 2
X=0
y = -2
y=0
x= =
il grafico è una retta
y
x
1/2
-2
y= x2-4x-3
Intersezioni asse x
y = x2-4x-3
y=0
y=0
Intersezione asse y
y = x2-4x-3
x=0
X=0
y=3
x2-4x-3 = 0
Δ = 16-12 = 4
X=
=
=3
=1
V (- ; ) = (2;-1)
y
2
4
x
-1
Studio del segno di una funzione
Per conoscere quali zone del piano cartesiano occupa una funzione bisogna studiarne il segno.
Si studia attraverso la disequazione f(x)
0
Poi si ombreggiano le zone del piano in cui non è presente il disegno
Esempio:
y
y = 3x-6
3x-6 ˃ 0
3x ˃6
x˃
x˃2
2
x
Funzione pari e funzione dispari
Sia D
R sottoinsieme di R t.c. se x € D allora – x € D
1. Si dice che f(x) è pari se risulta f(-x) = f(x), per tutte le x comprese in D
2. Si dice che f(x) è dispari se risulta f(-x) = - f(x), per tutte le x comprese in D
Conseguenza:
-x
x
Il grafico di una funzione pari è sempre simmetrico rispetto all’asse y
f(x)
-x
x
-f(x)
Il grafico di una funzione dispari è sempre simmetrico rispetto all’origine
N.B. esistono funzioni né pari né dispari.
Come si dimostra la parità/disparità di una funzione
Si va a sostituire –x ad x nella legge data e si vede cosa succede ed essa; può succedere che:
f(-x) = f(x)
-f(x)
f pari
f dispari
Altro né pari né dispari
Esempi
1) f(x) = 3/2 x
f(-x) = 3/2 (-x) = -3/2x = -f(x) dispari
tutte le rette per l’origine sono funzioni dispari
indipendentemente dal loro coefficiente angolare
x
0
2
4
6
-2
-4
y
0
3
6
9
-3
-6
y
x
2) f(x) = 2x-1
F(-x)= 2(-x)-1 = -2x -1
x y
0 -1
1 1
2 3
-1 -3
f(x)
né pari né dispari
y
x
Una retta qualunque non è né pari né dispari
3) f(x) =
f(-x) = (-x)2 = x2 =f(x) pari
y
x
0
-1
-2
1
2
y
0
1
4
1
4
x
Tutte le parabole con vertice nell’origine sono pari, indipendentemente dal valore di
4) f(x) = x2-1
f(-x) = (-x)2 -1 = + x2-1 = f(x)
x y
0 -1
-1 0
1 0
-2 3
2 3
pari
y
x
Le parabole corrispondenti a equazioni pure sono pari.
5) f(x) = x2 – x
f(-x) = (-x)2 – (-x) = x2+x
f(x) né pari né dispari
x
y
0
0
1
0
1/2 -1/2
y
x
Tutte le parabole corrispondenti a equazioni spurie sono né pari né dispari.
6) f(x) = x2 – 4x +3
f(-x) = (-x)2 -4 (-x)+3 = x2 +4x+3
x y
0 3
1 0
3 0
2 -1
f(x) né pari né dispari
y
x
Tutte le parabole corrispondenti a equazioni complete sono né pari né dispari
7) f(x) = |x|
f(-x) = |-x| = |x| = f(x) pari
x
-1
0
1
y
y
1
0
1
x
8) f(x) = x3
f(-x) = (-x)3 = -x3 = - f(x) dispari
x y
-1 -1
0 0
1 1
y
y
Schema studio funzione:
1.
2.
3.
4.
Determinare le condizioni di esistenza
Studio simmetrie
Intersezioni assi
Studio segno










