Laboratorio di Misure Fisiche per Scienze Biologiche
Esperienza n. 1 - Semplici misure di lunghezze e di tempi
Richiami di teoria
(Ragozzino et al Fondamenti di Fisica, Taylor Introduzione all'analisi degli errori)
- Grandezze fisiche. Misure dirette e indirette. Sensibilita' e precisione di uno
strumento. Unita' fondamentali e derivate. Sistemi di unita' di misura. Equazioni
dimensionali. Errori di misura. Errori assoluti ed errori relativi. Propagazione degli
errori: somme e differenze, prodotti e quozienti. Media e deviazione standard.
- Moto di un corpo: legge oraria, traiettoria.
- Velocita' media. Accelerazione media.
- Moto rettilineo uniforme e uniformemente accelerato
=====================================
Parte A - Verifica sperimentale della legge del moto di un proiettile
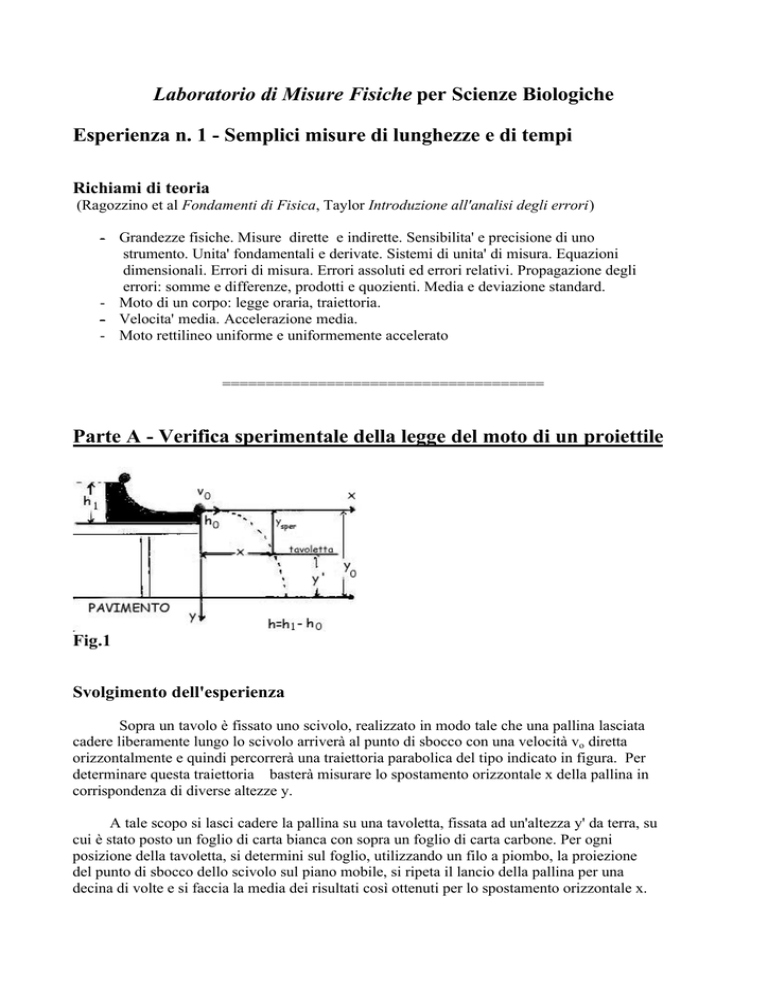
Fig.1
Svolgimento dell'esperienza
Sopra un tavolo è fissato uno scivolo, realizzato in modo tale che una pallina lasciata
cadere liberamente lungo lo scivolo arriverà al punto di sbocco con una velocità vo diretta
orizzontalmente e quindi percorrerà una traiettoria parabolica del tipo indicato in figura. Per
determinare questa traiettoria basterà misurare lo spostamento orizzontale x della pallina in
corrispondenza di diverse altezze y.
A tale scopo si lasci cadere la pallina su una tavoletta, fissata ad un'altezza y' da terra, su
cui è stato posto un foglio di carta bianca con sopra un foglio di carta carbone. Per ogni
posizione della tavoletta, si determini sul foglio, utilizzando un filo a piombo, la proiezione
del punto di sbocco dello scivolo sul piano mobile, si ripeta il lancio della pallina per una
decina di volte e si faccia la media dei risultati così ottenuti per lo spostamento orizzontale x.
Si misuri l'altezza y0 dello sbocco dello scivolo rispetto al pavimento e per ogni
posizione si misuri l'altezza y' della tavoletta sempre rispetto al pavimento, in modo da poter
determinare per differenza la corrispondente ordinata ysper .
In questo modo per differenti posizioni della tavoletta, si otterranno tante coppie di
valori (xi sper , yi sper ) che, riportati su carta millimetrata con i rispettivi errori, daranno la
traiettoria cercata.
Trattazione degli errori di misura
Ogni valore xi sper o yi sper , come ogni misura fisica, è affetto da errore.
xi sper è il risultato di una media di ≈ 10 misure e quindi, come dice la teoria degli errori, gli si puo'
attribuire come errore, l'errore quadratico medio della media (Ragozzino et al), anche detto
deviazione standard della media o errore standard della media (Taylor)
yi sper è il risultato della differenza fra 2 misure dirette eseguite con strumento a bassa sensibilità:
yi sper = yo - y'. Quindi applicando la legge di propagazione degli errori per le misure indirette,
l'errore da attribuire a yi sarà ∆yi = ∆y0 + ∆y' dove ∆y0 e ∆y' sono la sensibilità dello
strumento utilizzato per la misura.
Confronto con la curva teorica
Si riportino i dati ottenuti anche su carta bilogaritmica e si verifichi che la legge è
effettivamente una parabola (coeff. angolare della retta ≅ 2)
Considerando che il moto della pallina, dopo che ha abbandonato lo scivolo, è dato dalla
combinazione di un moto rettilineo uniforme lungo l'asse x e un moto rettilineo uniformemente
accelerato lungo l'asse y, con accelerazione uguale all'accelerazione di gravita' g (g=9.8 m/sec2),
dimostrare che in generale l'equazione teorica della traiettoria nel moto di un proiettile e' data da:
2
g
x
y = (tg ϑ0 ) x −
2
2
2
v
cos
ϑ
0
0
Trascurando l'attrito lungo lo scivolo e il moto di rotolamento della pallina, per il
1
principio di conservazione dell'energia meccanica mgh = mv 2 pertanto la velocità con cui
2
la pallina abbandona lo scivolo e' vo = 2 gh , dove h è indicato in Fig. 1. Sostituendo
nell'equazione della traiettoria e considerando che nel nostro caso θ0 = 0, l'equazione teorica
1 2
della traiettoria diventa: y teor =
x . Ricavare h ± ∆h e confrontare i dati sperimentali
4h
ottenuti con la curva teorica..
=====================================
Parte B - Piano inclinato
Scopo dell'esperienza e' quello di determinare l'accelerazione a cui e' sottoposto un
corpo che cade lungo un piano inclinato, misurando il tempo di passaggio fra due fotodioditraguardo collegati ad un cronometro digitale.
Prendendo come origine il punto di partenza in
cui la pallina e' collegata ad un elettromagnete e l'asse
y0 A
B
y parallelo al piano inclinato, la posizione della pallina
in funzione del tempo e' data da:
y
1
y = y 0 + v0 t + at 2
2
y − y0
1
= v0 + at da cui
t
2
e' possibile risalire al valore dell'accelerazione a anche senza misurare direttamente v0.
L'espressione precedente può essere linearizzata riscrivendola come
Svolgimento dell'esperienza:
a) Si determini il seno dell'angolo formato dal piano inclinato con il piano orizzontale
b) Si fissi il primo traguardo A della fotocellula. Fissato il traguardo B si misuri la loro
distanza (y - yo) ed il tempo impiegato dalla pallina a percorrerlo.
c) Si ripeta l'operazione una decina di volte, spostando il traguardo B in altra posizione.
d) Per ogni posizione del traguardo B si calcoli (y - yo) /t velocità media sul tratto AB e la si
riporti in un grafico in funzione di t.
e) Utilizzando il metodo della minima e massima pendenza, si individui la miglior retta
y= mx + n che approssima i punti sperimentali. Questa retta avrà come coefficiente
angolare m il valore 1/2 a e come intercetta n il valore vo della velocità di arrivo della
pallina nel punto A.
f) Si ricavi dal grafico il valore di a e quello di vo
g) Si confronti il valore dell'accelerazione cosi' trovata con il valore dell'accelerazione di
gravita'












