Analisi di un grafico spazio – tempo (s-t) nel moto vario

Analisi di un grafico spazio – tempo (s-t) nel moto vario
Il moto di un oggetto lungo una retta non sempre avviene a velocità costante, ma il suo moto è
vario, cioè la velocità cambia con il tempo.
Rappresentando su di un sistema di assi cartesiani, dove sull’ascisse è rappresentato il tempo,
mentre sull’asse delle ordinate è rappresentato la posizione del corpo, gli eventi riferiti al moto del
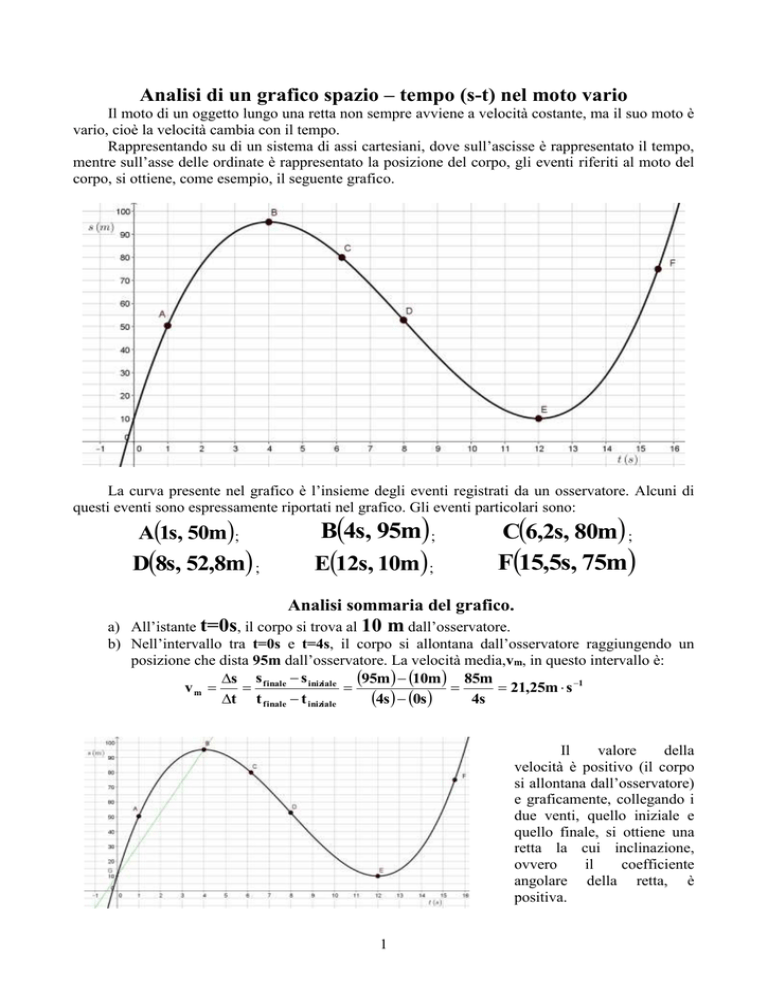
corpo, si ottiene, come esempio, il seguente grafico.
La curva presente nel grafico è l’insieme degli eventi registrati da un osservatore. Alcuni di
questi eventi sono espressamente riportati nel grafico. Gli eventi particolari sono:
A1s, 50m;
D8s, 52,8m ;
B4s, 95m ;
E12s, 10m ;
C6,2s, 80m ;
F15,5s, 75m
Analisi sommaria del grafico.
a) All’istante t=0s, il corpo si trova al 10 m dall’osservatore.
b) Nell’intervallo tra t=0s e t=4s, il corpo si allontana dall’osservatore raggiungendo un
posizione che dista 95m dall’osservatore. La velocità media,vm, in questo intervallo è:
s s finale  s iniziale 95m  10m 85m
vm 



 21,25m  s 1
4s  0s
t t finale  t iniziale
4s
Il
valore
della
velocità è positivo (il corpo
si allontana dall’osservatore)
e graficamente, collegando i
due venti, quello iniziale e
quello finale, si ottiene una
retta la cui inclinazione,
ovvero
il
coefficiente
angolare della retta, è
positiva.
1
c) Nell’intervallo di tempo tB=4s e tE=12s il corpo si sta avvicinando all’osservatore. La
velocità media vale:
s
s
s
s s
10m  95m   85m  10,6m  s 1
v m BE  BE  finale iniziale  E B 
12s  4s
t BE t finale  t iniziale t E  t B
8s
Il valore della velocità media è
negativa, allora il corpo si sta avvicinando
all’osservatore. Il coefficiente angolare
della retta passante per i due eventi B ed E
è negativo, quindi essa forma un angolo
ottuso con l’asse delle ascisse crescenti.
d) Nell’intervallo tE=12s e tF=15,5s il corpo si sta di nuovo allontanando dall’osservatore.
La velocità media tra gli eventi E ed F è:
s
s
s
s  s E 75m  10m 65m
v m EF   EF  finale iniziale  F


 18,6m  s 1
t EF t finale  t iniziale t F  t E 15,5s   12s  3,5s
Il valore della velocità è positivo, perciò il
corpo si sta allontanando dall’osservatore.
Osservando il grafico si nota che la retta
passante per i due eventi forma un angolo
acuto con l’asse delle ascisse crescenti,
pertanto il suo coefficiente angolare, il cui
valore coincide con quello della velocità
media, è positivo.
Osservazione
Dall’analisi del calcolo delle velocità medie e delle loro rappresentazioni grafiche si
possono effettuare le seguenti osservazioni:
1) Se l’angolo che la retta, congiungente due eventi, forma con l’asse delle ascisse
crescenti è acuto
allora
il
suo
coefficiente
angolare
è
positivo. Poiché il
coefficiente
angolare coincide
con il valore della
velocità
media,
allora
l’inclinazione
della retta fornisce, graficamente, una indicazione del suo valore (una piccola
2
inclinazione corrisponde un piccola velocità media; analogamente, ad una grande
inclinazione corrisponde un grande valore della velocità media.)
Nel grafico sono state disegnate tre rette con pendenze diverse e positive. I valori
delle pendenze corrispondono alle velocità medie tra due eventi. Inoltre le rette
formano angoli acuti con l’asse delle ascisse crescenti.
2) Se l’angolo formato dalla retta congiungente due eventi e dall’asse delle ascisse
crescenti è ottuso allora
il
suo
coefficiente
angolare è negativo,
pertanto
anche
la
velocità
media
è
negativa.
Nel grafico sono rappresentate
due rette entrambe con pendenze
negative e con angoli ottusi.
3) Se la retta è orizzontale, cioè parallela all’asse delle ascisse, la inclinazione è nulla e la
velocità media è anch’essa nulla.
Nel
grafico
è
evidenziata una retta
parallela all’asse delle
ascisse, che coincide con
l’asse del tempo. La
pendenza è nulla e la
velocità media è nulla.
Velocità istantanea
Dal grafico spazio – tempo oltre alle velocità medie è possibile calcolare, con grande
approssimazione, la velocità istantanea. Per velocità istantanea si intende la velocità che si calcola
nel caso in cui i due eventi che si prendono in considerazione sono vicinissimi tra di loro, cioè
l’intervallo di tempo, t, tende a zero. Da un punto di vista matematico la velocità istantanea è
definita come:
s
t 0 t
v is tan tan ea  v i  lim
Il significato è il seguente: la velocità istantanea è calcolata quando l’intervallo di tempo è
piccolissimo, cioè è una quantità che si avvicina a zero. È da tener presente che, affinché la velocità
3
istantanea abbia una valore ben definito, lo spazio percorso deve essere piccolissimo, cioè una
quantità tendente a zero.
Per fornire un metodo di calcolo e per giustificarlo, è necessario tener presente quanto detto in
precedenza circa il modo di trovare il valore della velocità media.
Si prende come
punto di riferimento
l’evento A. Inoltre si
considerano gli eventi
C, B, J e K.
Le velocità medie negli
intervalli di tempo tAC,
tAB, tAJ, tAK, sono:
v AC  5,7m  s 1
v AB  15m  s 1
v AJ  26,8m  s 1
v AK  31,9m  s 1
Man mano che l’intervallo di tempo diminuisce, la retta, passante per gli eventi iniziali e
finali, si avvicina sempre di più alla curva fino a diventare tangente ad essa nel punto A quando
l’intervallo di tempo tende a zero. Da questa osservazione si può tirar fuori una regola generale:
Per poter calcolare la velocità istantanea, si traccia la tangente alla curva nel punto
corrispondente all’evento considerato. Successivamente si calcola la pendenza della tangente,
il cui valore coincide con quello della velocità istantanea.
Un esempio illustrerà il metodo.
Il grafico da considerare è sempre lo stesso. Sul grafico si prende l’evento A e si vuole
calcolare
la
velocità
istantanea in tale punto. Per
effettuare il calcolo si
seguono i seguenti passi:
a) Nel punto A si
traccia la tangente
alla curva;
b) Sulla
retta
si
prendono
liberamente
due
punti, ad esempio L
ed M. Per un calcolo
il
più
preciso
possibile, i due punti
devono
essere
distanti tra di loro.
c) Si individuano, con
la migliore approssimazione possibile, le coordinate dei due punti. Nel caso in esame le
coordinate sono:
M 1s,  15m
L4s, 150m ;
4
d) Si calcola la pendenza della retta, ovvero il coefficiente angolare. Tale valore coincide con
la velocità istantanea, vA.
s
s s
150m   15m  150m  15m  165m  33m  s 1
v A  LM  L M 
4s   1s
t LM t L  t M
4s  1s
5s
-1
Pertanto la velocità istantanea nel punto A è di 33ms .
La positività della velocità poteva essere prevista poiché la retta tangente alla curva
forma un angolo acuto con l’asse delle ascisse crescenti.
Con lo stesso metodo si possono calcolare le velocità istantanee in qualsiasi istante. In
particolare saranno evidenziate le rette tangenti ed elencati i valori delle velocità nei punti B,
C, D, E ed F.
Nel grafico
sono evidenziate
parti delle tangenti
nei punti A, B, C,
D, E ed F.
Nei punti A ed F
le rette tangenti
formano
angoli
acuti con l’asse
delle
ascisse
crescenti, per cui
le velocità sono
positive:
v A  33m  s 1
v F  40,8m  s 1
Nei punti B ed E, le rette tangenti sono parallele all’asse delle ascisse, l’inclinazione è
nulla, per cui le velocità istantanee sono nulle.
v B  0m  s 1 ;
v E  0m  s 1
Negli istanti di tempo
t B  4s ;
t E  12s
il corpo è fermo.
Nei punti C e D il corpo sta tornando verso l’osservatore e la sua velocità è negativa.
Inoltre le due tangenti formano un anglo ottuso con l’asse delle ascisse crescenti. I valori
delle velocità istantanee sono:
v C  12,6m  s 1 ;
v D  16m  s 1
5