Analisi di quadripoli nel dominio del tempo

LEZIONI DI ELETTRONICA
per la classe 5° informatica
Prof. Eros Rambelli
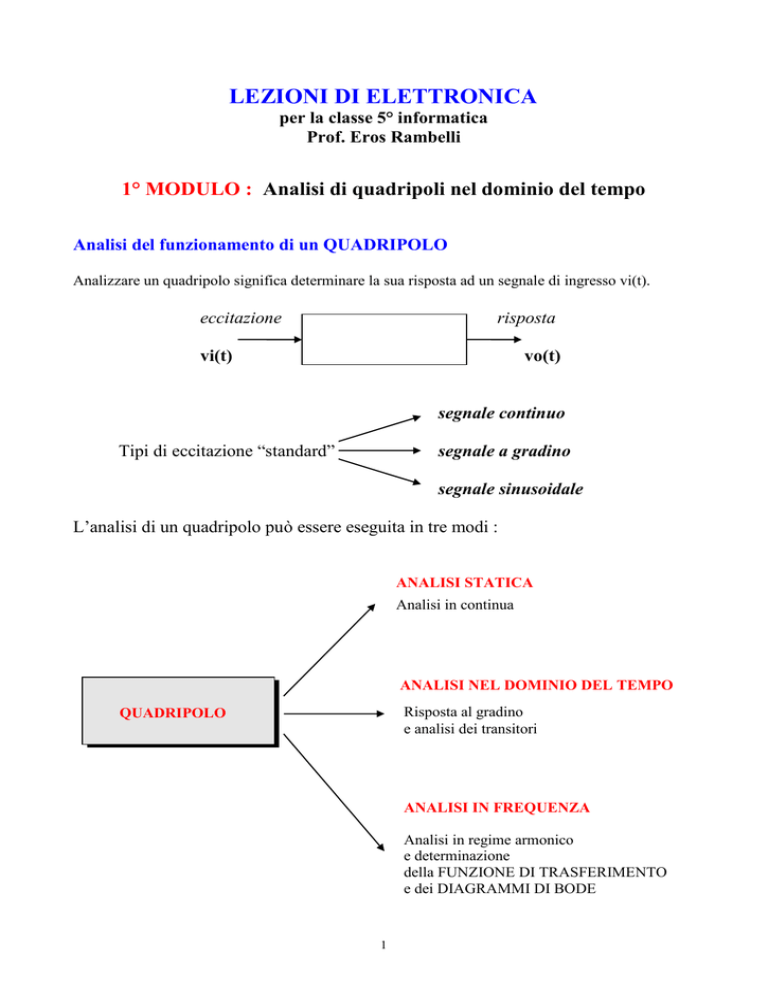
1° MODULO : Analisi di quadripoli nel dominio del tempo
Analisi del funzionamento di un QUADRIPOLO
Analizzare un quadripolo significa determinare la sua risposta ad un segnale di ingresso vi(t).
eccitazione
risposta
QUADRIPOLO
vi(t)
vo(t)
segnale continuo
Tipi di eccitazione “standard”
segnale a gradino
segnale sinusoidale
L’analisi di un quadripolo può essere eseguita in tre modi :
ANALISI STATICA
Analisi in continua
ANALISI NEL DOMINIO DEL TEMPO
Risposta al gradino
e analisi dei transitori
QUADRIPOLO
ANALISI IN FREQUENZA
Analisi in regime armonico
e determinazione
della FUNZIONE DI TRASFERIMENTO
e dei DIAGRAMMI DI BODE
1
SISTEMI FISICI LINEARI
Nei sistemi fisici lineari le relazioni tra le variabili sono di tipo lineare.
I sistemi fisici lineari di suddividono in due categorie principali : sistemi proporzionali
sistemi differenziali
1. SISTEMI DI TIPO PROPORZIONALE
Un sistema fisico di tipo proporzionale è un sistema in cui il segnale di uscita è proporzionale al
segnale di ingresso.
f(t)
g(t)
g(t) = K f(t)
ESEMPIO
f(t)
Nei sistemi
proporzionali
il segnale di
uscita ha la
stessa forma
di quello di
ingresso
t
g(t)
t
2. SISTEMI DI TIPO “DIFFERENZIALE” DEL 1° ORDINE
Un sistema fisico di tipo differenziale del 1° ordine è un sistema in cui il segnale di uscita è
proporzionale alla velocità di variazione del segnale di ingresso.
f(t)
g(t)
g(t) = K df(t)/dt
2
ESEMPIO
f(t)
Nei sistemi
differenziali
il segnale di
uscita ha
generalmente
una forma
diversa da
quello di
ingresso.
t
g(t)
Solo i segnali
sinusoidali ed
esponenziali
del tipo
ekx o e-kx
forniscono in
uscita un
segnale della
stessa forma
t
SISTEMI ELETTRICI LINEARI
In campo elettrico i componenti lineari fondamentali sono :
resistore
condensatore
induttore
Relazione tensione-corrente per i componenti elettrici lineari :



resistore
condensatore
induttore
v(t) =
i(t) =
v(t) =
R i(t)
C dv(t) / dt
L di(t) / dt
R resistenza
C capacità
L induttanza
(ohm)
(farad)
(henry)
Esercizio
Per un resistore, un condensatore e un induttore disegnare l’andamento di v(t) e i(t) nel caso in cui
la tensione sia : onda triangolare
onda sinusoidale
onda quadra
3
SISTEMI ELETTRICI DEL 1° ORDINE
Un sistema del 1° ordine è un sistema in cui sono presenti uno o più elementi di tipo proporzionale
e un unico elemento di tipo differenziale.
In un sistema del primo ordine, la relazione ingresso-uscita è espressa da una equazione
differenziale di 1° grado.
In campo elettrico sono sistemi del primo ordine quei quadripoli in cui sono presenti uno o più
resistori e un unico condensatore o un unico induttore.
Esempi di quadripoli del 1° ordine
R
1. Circuito R-C
Vr(t)
C
Vi(t)
Vo(t)
Relazione ingresso-uscita
vi(t) = vr (t) + vo(t)
i(t) = v r (t) / R = vi(t) / R - vo(t)/R
i(t) = C dvo (t) / dt
vi(t) = vo(t) + RC dvo (t) / dt
vi(t) = vo(t) +  dvo (t) / dt
con  = RC
R
2. Circuito R-L
Vr(t)
L
Vi(t)
Vo(t
)
Relazione ingresso-uscita
vo(t) = L di(t)/dt
i(t) = vR (t) / R = vi(t) / R - vo(t) / R
vo(t) = L/R dvi(t)/dt - L/R dvo(t)/dt
L/R dvo(t)/dt + vo(t) = L/R dvi(t)/dt
 dvo(t)/dt + vo(t) =  dvi(t)/dt
con  = L/R
ESERCIZIO
Nei due circuiti precedenti scambiare i componenti tra loro e determinare la nuova relazione
ingresso-uscita.
Confrontare tra loro i risultati ottenuti.
4
RISPOSTA AL GRADINO DI UN SISTEMA DEL 1° ORDINE
Se il segnale di ingresso di un sistema del 1° ordine è un segnale a gradino,
vi(t)
t
La risoluzione delle equazioni differenziali sopra ricavate porta in ogni caso al seguente risultato :
il segnale in uscita è una esponenziale del tipo :
-t/
vo(t) = A + B e
[1]
 = costante di tempo
il valore di  dipende dalle caratteristiche del sistema
Si tratta di una curva che parte (t=0) dal valore A + B e tende asintoticamente al valore A.
L’intervallo di tempo richiesto affinchè la curva raggiunga il valore dell’asintoto è chiamato
transitorio.
La durata del transitorio è in teoria infinito, però dopo un tempo pari a 5 curva e asintoto sono
quasi coincidenti, per cui si ritiene che il transitorio sia completato.
Siccome :
A + B = vo(0) = Vin
A
= vo() = Vfin
valore iniziale di vo(t) (subito dopo il gradino)
valore finale di vo(t)
(a transitorio completato)
l’equazione [1] può essere scritta nel seguente modo :
[2]
-t/
vo(t) = Vfin - (Vfin - Vin) e
Nell’analisi dei sistemi R-C e R-L faremo sempre riferimento a questa espressione.
In questi sistemi  = RC o  = L/R
N.B.
Se il gradino di ingresso si presenta in un istante To diverso da zero, l’espressione del transitorio è
la seguente :
-(t -To)/
vo(t) = Vfin - (Vfin - Vin) e
5
RISPOSTA AL GRADINO DI QUADRIPOLI RC A VUOTO
1. Quadripolo RC (passa-basso)
vi(t)
R
Vr(t)
C
Vi(t)
Vo(t)
t
Vin = 0
Vfin = E
vo(t) = E - E e
vo(t)
 = RC
-t/
t
2. Quadripolo CR (passa-alto)
C
vi(t)
R
Vi(t)
E
Vo(t)
t
Vin = E
Vfin = 0
vo(t)
 = RC
E
-t/
vo(t) = E e
t
ESERCIZI
1. Nei circuiti precedenti sostituire il condensatore con un induttore e ricavare la risposta al
gradino.
2. Nei circuiti precedenti ricavare la risposta al seguente gradino di ingresso :
vi(t)
E1
t
-E2
6
RISPOSTA AL GRADINO DI QUADRIPOLI RC A CARICO
1. Quadripolo RC (passa-basso)
Un carico resistivo collegato al quadripolo determina :
 attenuazione
 riduzione della costante di tempo 
Dimostrazione
Quadripolo RC a carico
Circuito equivalente di Thevenin
R
Vi
Req
C
Ro R
Req = ---------Ro + R
Ro
C
Veq
Vo
Ro
Veq = ---------- Vi = KA Vi
R + Ro
Risposta al gradino :
vi(t)
E
t
Veq = 0
per t < 0
vo(t) = Veq – Veq e–t/
e
Veq = KA E

vo(t) = Veq (1 – e–t/ )

vo(t) = KA E (1 – e –t/)
2. Quadripolo CR (passa-alto)
Un carico resistivo collegato al quadripolo determina :
 riduzione della costante di tempo 
 ma non attenuazione
Svolgere la dimostrazione come esercizio.
7
per t  0
con
 = Req C
Vo
RISPOSTA AL SEGNALE IMPULSIVO DI QUADRIPOLI DEL 1°ORDINE
Nel caso il segnale di ingresso sia un impulso squadrato, dobbiamo tener conto dei transitori che si
verificano sui due fronti.
Impulso di ingresso:
vi(t)
con To = durata dell’impulso
E
t
To
1°
To  5

il primo transitorio si esaurisce
2°
To < 5

il primo transitorio non si esaurisce
Possono verificarsi due casi :
1° caso
I due transitori sono indipendenti e hanno lo stesso andamento visto in precedenza.
2° caso
Trascorso il tempo To, il segnale di uscita non avrà raggiunto il suo asintoto, ma assumerà un
determinato valore E1, calcolabile dall’espressione del primo transitorio, sostituendo a t il valore
To.
In base a questo valore e tenendo conto delle caratteristiche del quadripolo sarà possibile
determinare la Vin del secondo transitorio.
ESERCIZI
1. Determinare e disegnare la risposta ad un impulso del tipo indicato sopra di un quadripolo RC
passa-basso, nei seguenti casi : To = 10 
To = 5 
To = 
2. Determinare e disegnare la risposta ad un impulso del tipo indicato sopra di un quadripolo CR
passa-alto, nei seguenti casi : To = 10 
To = 5 
To = 
8
RISPOSTA AL GRADINO E ALL’IMPULSO RETTANGOLARE
DI QUADRIPOLI RC A VUOTO E A CARICO
ESERCIZI 1
N. 1
A)
B)
R
A
B
A
VR
C
VC
C
Vi
VC
R
Vi
C
Generatore ideale
R = 500 
B
VR
C
Quadripolo RC
Generatore ideale
Quadripolo CR
C = 100 nF
In entrambi i quadripoli ricavare e disegnare l’andamento di VR e VC in funzione del tempo nei seguenti
casi :
a)
Vi = -2 V
per t < 0
e
per t  0
Vi = +4 V
b)
Vi (V)
Vi (V)
4
4
0.5
t (ms)
0.05
t (ms)
c)
Vi (V)
Vi (V)
4
4
1
2
3
4
t (ms)
9
0.05
0.1
0.15
t (ms)
N. 2
A)
B)
R
A
B
A
C
B
VR
C
Vi
Ro
VC
Vo
Vi
C
Generatore ideale
R = 500 
R
Ro
Vo
C
Quadripolo RC
Carico
Generatore ideale
Quadripolo CR
Carico
Ro = 500 
C = 100 nF
1. In entrambi i quadripoli ricavare e disegnare l’andamento di Vo in funzione del tempo nei seguenti
casi :
a)
Vi = -4
per t < 0
e
per t  0
Vi = +4 V
b)
Vi (V)
Vi (V)
4
4
0.5
t (ms)
0.05
t (ms)
c)
Vi (V)
Vi (V)
4
4
1
2
3
4
t (ms)
0.05
0.1
2. Per il circuito A) disegnare anche la VR nel caso in cui il segnale abbia l’andamento a).
3. Per il circuito B) disegnare anche la VC nel caso in cui il segnale abbia l’andamento a).
10
0.15
t (ms)
ESERCIZI 2
Rg
Rl
A
Vg
B
Cl
Vi
Rg = 50 
Rl = 50 
Cl = 1 F
Ro = 100 
Ro
Vo
C
Driver
Interconnessione
Receiver
N. 1
Con
Vg = 0
per t < 0
e
Vg = +4 V
per t  0
1. Ricavare l’espressione di Vi e Vo in funzione del tempo a vuoto (TA) e a carico (TC).
2. Disegnare Vg, Vi e Vo in funzione del tempo a vuoto e a carico.
3. A vuoto (TA) determinare dopo quanto tempo la tensione Vo raggiunge il valore di 3 V.
N. 2
Nei casi in cui Vg vari nel tempo nel modo seguente :
Vg(t)
Vg(t)
4
4
0.5
t (ms)
0.1
t (ms)
1. Determinare il valore massimo raggiunto da Vo a vuoto e a carico
2. Disegnare l’andamento di Vo a vuoto e a carico
N. 3
Nei casi in cui Vg vari nel tempo nel modo seguente :
Vg(t)
Vg(t)
4
4
1
2
3
4
t (ms)
1. Disegnare l’andamento di Vo(t) a vuoto.
11
0.1
0.2
0.3
t (ms)