Specializzazione Informatica Abacus Corso di elettronica classe 5°

Specializzazione Informatica Abacus
Corso di elettronica
classe 5°
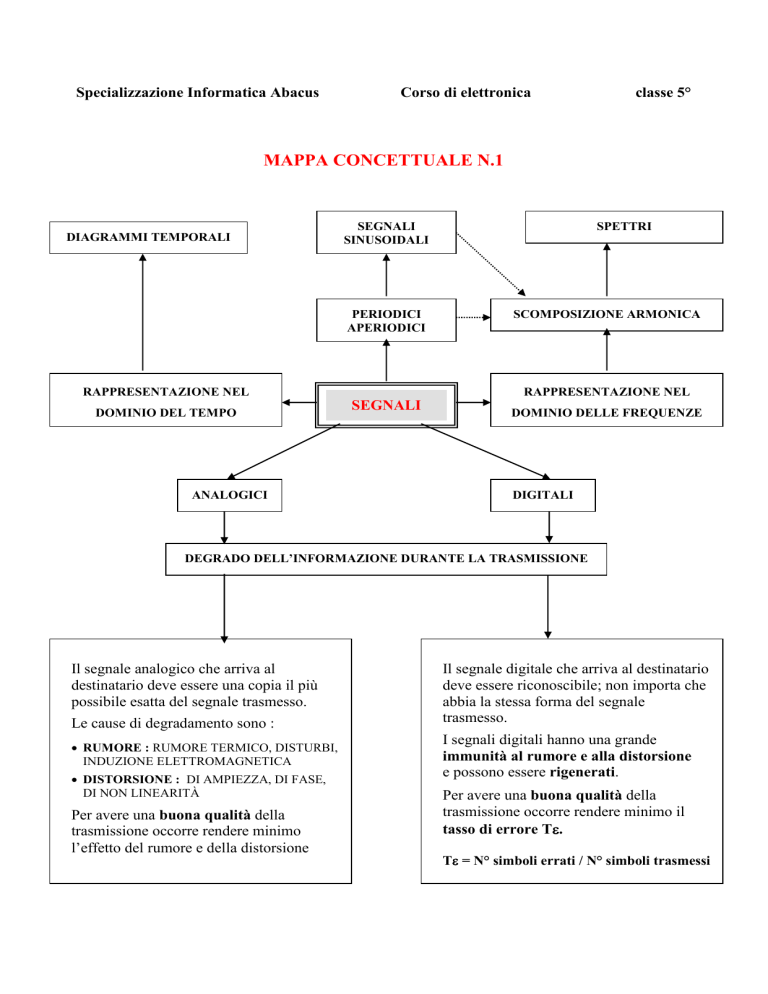
MAPPA CONCETTUALE N.1
DIAGRAMMI TEMPORALI
SEGNALI
SINUSOIDALI
PERIODICI
APERIODICI
RAPPRESENTAZIONE NEL
DOMINIO DEL TEMPO
ANALOGICI
SPETTRI
SCOMPOSIZIONE ARMONICA
RAPPRESENTAZIONE NEL
SEGNALI
DOMINIO DELLE FREQUENZE
DIGITALI
DEGRADO DELL’INFORMAZIONE DURANTE LA TRASMISSIONE
Il segnale analogico che arriva al
destinatario deve essere una copia il più
possibile esatta del segnale trasmesso.
Le cause di degradamento sono :
 RUMORE : RUMORE TERMICO, DISTURBI,
INDUZIONE ELETTROMAGNETICA
 DISTORSIONE : DI AMPIEZZA, DI FASE,
DI NON LINEARITÀ
Per avere una buona qualità della
trasmissione occorre rendere minimo
l’effetto del rumore e della distorsione
Il segnale digitale che arriva al destinatario
deve essere riconoscibile; non importa che
abbia la stessa forma del segnale
trasmesso.
I segnali digitali hanno una grande
immunità al rumore e alla distorsione
e possono essere rigenerati.
Per avere una buona qualità della
trasmissione occorre rendere minimo il
tasso di errore T.
T = N° simboli errati / N° simboli trasmessi
Specializzazione Informatica Abacus
Corso di elettronica
classe 5°
MAPPA CONCETTUALE N.2
SEGNALE ARMONICO
Segnale formato da
un’unica sinusoide
v(t) = VM sen (2ft  )
v(t) valore istantaneo
VM
ampiezza
f
frequenza

sfasamento
+
anticipo
– ritardo
t tempo (variabile indipendente)
Disegnare il segnale
 Nel dominio del tempo
 Nel dominio delle
frequenze (spettro di
ampiezza e di fase)
Valor medio = 0
_
Valore efficace = VM / 2
Segnale armonico
con valor medio
diverso da zero
Se un segnale armonico
entra in un quadripolo
lineare, può essere
attenuato, amplificato,
sfasato, ma non distorto.
v(t) = Vm + VM sen (2ft  )
Vm valor medio
RELAZIONE
INGRESSO-USCITA
QUADRIPOLO LINEARE
Quadripolo formato da:
resistori, condensatori,
induttori, amplificatori lineari.
 Dominio del tempo :
equazione differenziale
 Dominio delle frequenze :
funzione complessa di f
(funzione di trasferimento)
Generalmente un quadripolo
lineare ha una banda passante
limitata (passa-basso, passa-alto,
passa-banda).
Saper determinare
l’attenuazione e lo
sfasamento introdotto
da un quadripolo
lineare su un segnale
armonico
Saper ricavare la funzione di
trasferimento di un quadripolo
del 1° ordine passa-basso o
passa-alto.
Saper ricavare dalla funzione
di trasferimento l’espressione
del guadagno e dello
sfasamento e saperle
rappresentare.
Specializzazione Informatica Abacus
Corso di elettronica
classe 5°
MAPPA CONCETTUALE N.3
SEGNALE
COMPLESSO
SEGNALE PERIODICO
Segnale non
sinusoidale
È composto da

SEGNALE NON PERIODICO
È composto da
infinite armoniche con
frequenze che possono
assumere tutti gli infiniti valori
compresi in un certo range.
una costante (valor
medio)

infinite armoniche di
frequenza multipla di
quella del segnale con
ampiezza via via
decrescente
Serie di Fourier
Trasformata di Fourier
f
f
Se un segnale complesso entra in un quadripolo lineare a banda limitata viene
distorto :
 Dominio del tempo : il segnale di uscita ha una forma diversa

Dominio delle frequenze : il segnale di uscita ha spettri diversi
Distorsione di ampiezza e di fase



Un segnale che varia velocemente ha uno “spettro largo”
Un segnale che varia lentamente ha uno “spettro stretto”
Un segnale impulsivo ha una banda spettrale infinita, ma la banda informativa è limitata ed è
compresa tra 0 e fz (frequenza di cifra) ed è inversamente proporzionale alla durata degli
impulsi :
fz = 1/T0
MAPPA CONCETTUALE N. 4 : CIRCUITI RC
Se un circuito è costituito da una sola maglia
con un unico generatore di tensione, la forza
elettromotrice del generatore è uguale alla
somma delle cadute di tensione sugli elementi
passivi presenti nella maglia.
(2° principio di Kirchhoff).
In regime variabile le relazioni
tensione-corrente sono la seguente :
RESISTENZA :
CONDENSATORE :
Quando si collega un carico resistivo ad un bipolo
attivo o ad un quadripolo si ha ATTENUAZIONE
Solo se la resistenza interna del bipolo o quella di
uscita del quadripolo è trascurabile rispetto a quella
del carico non c’è attenuazione
In continua, un condensatore si comporta come un
interruttore aperto
v(t) = R i(t)
i(t) = C dv(t) / dt
In continua, i filtri RC
passa-basso si
comportano come degli
attenuatori :
Un condensatore
per variare la
tensione ai suoi
capi ha bisogno
di tempo.
a vuoto
vo(t) = vi(t)
a carico
con A < 1
vo(t) = Avi(t)
Quando in ingresso ad un circuito RC
viene applicato un gradino, le tensioni
vC(t) e vR(t) si portano alla nuova
situazione di equilibrio in un certo
tempo (transitorio) con una legge di
tipo esponenziale :
In continua, i filtri
RC passa-alto non
lasciano passare il
segnale :
vo(t) = 0 in ogni
caso
Finito il transitorio, la situazione è
quella che ci sarebbe in continua, con
un segnale di ingresso pari a quello
che c’è dopo il gradino.
La Vfin si determina tenendo conto di
ciò.
v(t) = Vfin + (Vin – Vfin) e-t/ a
con  = RC costante di tempo
In un circuito RC del 1° ordine funzionante a vuoto, la situazione immediatamente
successiva al presentarsi di un gradino in ingresso (Vin) è la seguente:

la vC(t) è uguale a quella precedente al gradino;

la vR(t) è uguale a quella precedente al gradino sommata algebricamente al gradino
di ingresso (l’effetto si fa sentire tutto sulla resistenza).
Se il segnale di ingresso presenta un secondo gradino
prima che il transitorio sia esaurito, per conoscere la
situazione immediatamente successiva al secondo gradino
occorre determinare (mediante la funzione esponenziale) i
valori a cui erano giunti vC(t) e vR(t) immediatamente prima.
A carico la costante di tempo diminuisce :
 = Req C
con Req = R RL
Specializzazione Informatica Abacus
Corso di elettronica
classe 5°
MAPPA CONCETTUALE N. 5
ANALISI DI CIRCUITI ELETTRICI IN REGIME SINUSOIDALE
Dominio del tempo
per qualsiasi segnale
Relazione tensione-corrente
v(t) = R i(t)
i(t) = C dv(t) / dt
v(t) = L di(t) / dt
Dominio del tempo
per segnali sinusoidali
Dominio
delle frequenze
relazioni vettoriali
v(t) = VM sen t
V = VM 0
i(t) = IM sen t
IM = VM / R
I =V/R
i(t) = IM cos t
IM = CVM
I = j CV
i(t) = - IM cos t
IM = VM / L
I = V / j L
Darne una spiegazione
Saperle ricavare
con la regola della
derivazione
Interpretarne il significato
Saperle ricavare
Interpretarne il
significato
Interpretarne il significato
Saperle rappresentare
graficamente
Saperle
rappresentare
con diagrammi
vettoriali
IMPEDENZA
Z=V/I
V= ZI
resistenza
condensatore
induttanza
Z=R
Z = -j 1/C = -j XC
Z = jL = j XL
V= RI
V = -j XC I
V = j XL I
In regime sinusoidale, quando si esegue l’analisi vettoriale dei circuiti elettrici,
valgono gli stessi principi visti per i sistemi in continua.
Le relazioni che si ottengono sono però di tipo complesso.
Specializzazione Informatica Abacus
Corso di elettronica
classe 5°
MAPPA CONCETTUALE N. 6
ANALISI IN FREQUENZA DEI QUADRIPOLI LINEARI
vi(t)
vo(t)
QUADRIPOLO LINEARE
R-L-C
vi(t) sinusoidale
vo(t) sinusoidale
Vo / Vi = f()
vi(t) = Vi sen (t + i)
vo(t) = Vo sen (t + o)
o - i = ()
 stessa frequenza di vi(t)
 ampiezza e fase diverse
Per descrivere il funzionamento
di un quadripolo lineare
al variare della frequenza
del segnale di ingresso
occorre conoscere
f() e ()
Per determinare f() e ()
abbiamo due metodi :
- metodo vettoriale
- metodo delle trasformate di Fourier
Entrambi i metodi ci permettono di determinare una funzione complessa di  :
F(j )
di modulo F() e argomento ( )
Questa funzione complessa è detta Funzione di Trasferimento
Corso di elettronica
COME SI ESEGUE L’ANALISI IN FREQUENZA
SOSTITUZIONE
dei CONDENSATORI e delle INDUTTANZE
con le rispettive REATTANZE
C
-j / C
L
JL
DETERMINAZIONE
del VETTORE DI USCITA Vo
in funzione del VETTORE DI INGRESSO Vi
applicando i principi dell’elettrotecnica
CALCOLO
per determinare la
FUNZIONE DI TRASFERIMENTO
nella forma più adeguata per l’analisi successiva
Vo / Vi = F (j)
DETERMINAZIONE del MODULO e della FASE
della FUNZIONE DI TRASFERIMENTO
in funzione di 
RAPPRESENTAZIONE GRAFICA
del modulo e della fase della funzione di trasferimento
DIAGRAMMI DI BODE