Esercizio 3. Oscillatore a sfasamento. Frequenza di oscillazione.

Esercizio 3
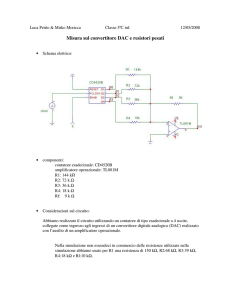
Ricavare la frequenza di oscillazione e la condizione di innesco dell’oscillatore a sfasamento di
figura 1.
Figura 1 Oscillatore a sfasamento.
Svolgimento
Il circuito composto dall’amplificatore operazionale U2, dalla resistenza R0 e dal condensatore C
collegato al nodo A è un derivatore e sfasa il segnale proveniente dal nodo A di -90o. Affinché sia
soddisfatta la condizione di Barkhausen che riguarda la fase (ricordiamo che deve essere nulla) le
due celle RC poste tra i punti A e B devono sfasare complessivamente di 90o. Dato che sono uguali
ciascuna produrrà uno sfasamento di 45o. Questo avverrà alla frequenza di oscillazione.
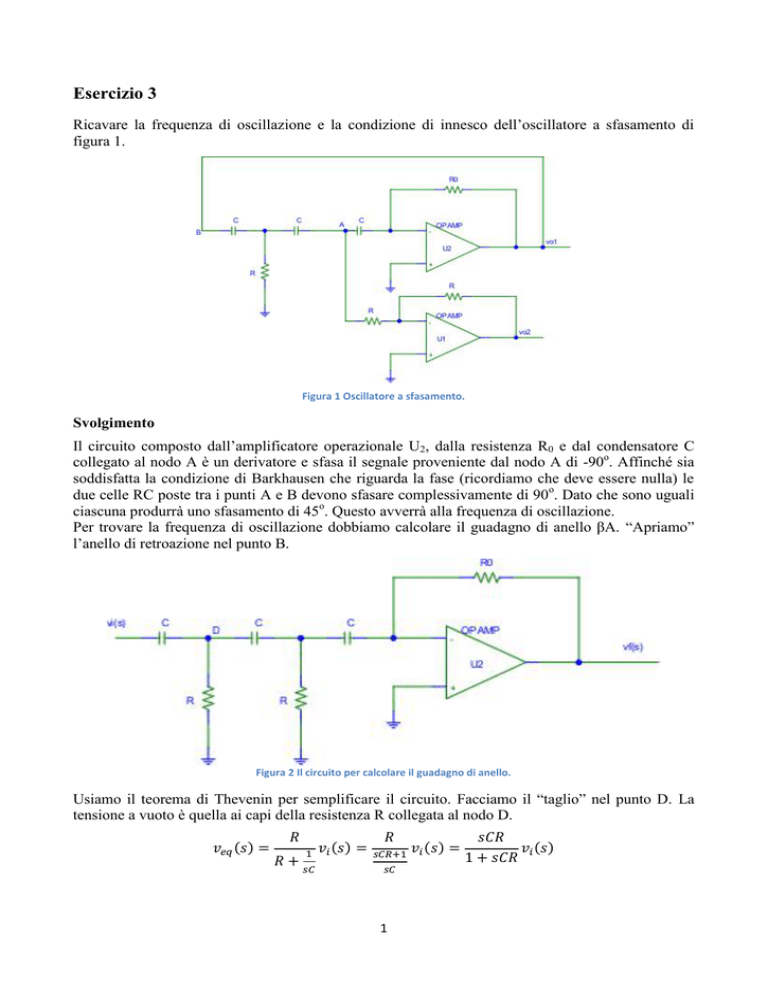
Per trovare la frequenza di oscillazione dobbiamo calcolare il guadagno di anello βA. “Apriamo”
l’anello di retroazione nel punto B.
Figura 2 Il circuito per calcolare il guadagno di anello.
Usiamo il teorema di Thevenin per semplificare il circuito. Facciamo il “taglio” nel punto D. La
tensione a vuoto è quella ai capi della resistenza R collegata al nodo D.
𝑣𝑒𝑞 (𝑠) =
𝑅
1
𝑅 + 𝑠𝐶
𝑣𝑖 (𝑠) =
𝑅
𝑠𝐶𝑅+1
𝑠𝐶
1
𝑣𝑖 (𝑠) =
𝑠𝐶𝑅
𝑣 (𝑠)
1 + 𝑠𝐶𝑅 𝑖
L’impedenza equivalente è data da:
𝑅
𝑍𝑒𝑞 =
𝑠𝐶
𝑅
1
𝑅 + 𝑠𝐶
=
𝑠𝐶
𝑠𝐶𝑅+1
𝑠𝐶
=
𝑅
1 + 𝑠𝐶𝑅
Ridisegniamo il circuito:
Figura 3 Il circuito semplificato con il teorema di Thevenin.
Adesso applichiamo nuovamente il teorema di Teorema di Thevenin. Questa volta facciamo il
“taglio” al nodo E.
La tensione a vuoto è quella ai capi della resistenza R:
𝑣𝑒𝑞1 (𝑠) =
𝑅
1
𝑅 + 𝑠𝐶 + 𝑍𝑒𝑞
𝑣𝑒𝑞 (𝑠) = 𝑠𝐶𝑅+1
𝑠𝐶
𝑅
𝑅
+ 1+𝑠𝐶𝑅
𝑣𝑒𝑞 (𝑠) =
𝑠𝐶𝑅(1 + 𝑠𝑅𝐶)
𝑣 (𝑠) =
1 + 2𝑠𝐶𝑅 + 𝑠 2 𝑅 2 𝐶 2 + 𝑠𝑅𝐶 𝑒𝑞
Sostituendo alla tensione a vuoto il valore precedentemente calcolato si trova:
𝑠𝐶𝑅(1 + 𝑠𝑅𝐶)
𝑠𝐶𝑅
𝑠 2𝑅2𝐶 2
(𝑠)
𝑣
=
𝑣 (𝑠)
1 + 3𝑠𝐶𝑅 + 𝑠 2 𝑅 2 𝐶 2 1 + 𝑠𝐶𝑅 𝑖
1 + 3𝑠𝐶𝑅 + 𝑠 2 𝑅 2 𝐶 2 𝑖
Impedenza equivalente:
=
1
𝑍𝑒𝑞1 =
(𝑍𝑒𝑞 + 𝑠𝐶 ) 𝑅
1
𝑍𝑒𝑞 + 𝑠𝐶 + 𝑅
𝑅
=
𝑅
1+𝑠𝐶𝑅
(𝑠𝐶𝑅+1+𝑠𝐶𝑅)𝑅
1
(1+𝑠𝐶𝑅 + 𝑠𝐶) 𝑅
1
+ 𝑠𝐶 + 𝑅
=
(1+𝑠𝐶𝑅)𝑠𝐶
𝑠𝐶𝑅+1+𝑠𝐶𝑅+𝑠𝐶𝑅+𝑠2 𝐶 2 𝑅 2
(1+𝑠𝐶𝑅)𝑠𝐶
=
(1 + 2𝑠𝐶𝑅)𝑅
1 + 3𝑠𝐶𝑅 + 𝑠 2 𝐶 2 𝑅 2
Ridisegniamo nuovamente il circuito:
Figura 4 Il circuito semplificato dopo la seconda applicazione del teorema di Thevenin.
Adesso si vede chiaramente che la tensione di feedback è quella applicata ai capi di R0. Per
determinarla dobbiamo trovare la corrente I0.
2
Questa corrente, dato che l’amplificatore operazionale è ideale, è la stessa che scorre nella serie
Zeq1–C ed è data da:
𝐼0 =
𝑣𝑒𝑞1 (𝑠)
1
𝑍𝑒𝑞1 + 𝑠𝐶
1
=
(1+2𝑠𝐶𝑅)𝑅
1
+ 𝑠𝐶
1+3𝑠𝐶𝑅+𝑠2 𝐶 2 𝑅 2
𝑠 2𝑅2𝐶 2
𝑣 (𝑠) =
1 + 3𝑠𝐶𝑅 + 𝑠 2 𝑅 2 𝐶 2 𝑖
𝑠 2𝑅2𝐶 2
= 𝑠𝐶𝑅+2𝑠2 𝐶 2 𝑅2 +1+3𝑠𝐶𝑅+𝑠2 𝐶 2 𝑅2
𝑣 (𝑠) =
1 + 3𝑠𝐶𝑅 + 𝑠 2 𝑅 2 𝐶 2 𝑖
1
𝑠𝐶(1+3𝑠𝐶𝑅+𝑠2 𝐶 2 𝑅 2 )
1
=
1+4𝑠𝐶𝑅+3𝑠2 𝐶 2 𝑅 2
𝑠𝐶(1+3𝑠𝐶𝑅+𝑠2 𝐶 2 𝑅 2 )
=
𝑠 2𝑅2𝐶 2
𝑣 (𝑠) =
1 + 3𝑠𝐶𝑅 + 𝑠 2 𝑅 2 𝐶 2 𝑖
(1 + 3𝑠𝐶𝑅 + 𝑠 2 𝐶 2 𝑅 2 )
𝑠 2𝑅2𝐶 2
𝑣 (𝑠) =
1 + 3𝑠𝐶𝑅 + 𝑠 2 𝑅 2 𝐶 2 𝑖
1+4𝑠𝐶𝑅+3𝑠2 𝐶 2 𝑅 2
𝑠𝐶
=
𝑠 2𝑅2𝐶 2
𝑣 (𝑠) =
1+4𝑠𝐶𝑅+3𝑠2 𝐶 2 𝑅 2 𝑖
𝑠𝐶
=
𝑠 2𝑅2𝐶 2
1
1
1
1
4
𝑠 2 𝑅 2 𝐶 2 (𝑠2 𝑅2 𝐶 2 + 𝑠𝐶𝑅 + 3)
𝑠𝐶
1
4
(
+ 𝑠𝐶𝑅 + 3)
𝑠𝐶 𝑠2 𝑅 2 𝐶 2
𝑣𝑖 (𝑠) =
𝑣𝑖 (𝑠)
Finalmente possiamo trovare la tensione di feedback:
𝑣𝑓 (𝑠) =
𝑅0
1
1
4
(
+ 𝑠𝐶𝑅 + 3)
𝑠𝐶 𝑠2 𝑅 2 𝐶 2
𝑣𝑖 (𝑠)
E il guadagno di anello (tenendo presente che l’amplificatore operazionale è in configurazione
invertente):
𝛽𝐴 =
𝑣𝑓 (𝑠)
=−
𝑣𝑖 (𝑠)
𝑅0
1
1
4
(
+ 𝑠𝐶𝑅 + 3)
𝑠𝐶 𝑠2 𝑅 2 𝐶 2
Quindi:
𝛽𝐴(𝑗𝜔) = −
𝑅0
1
1
(
𝑗𝜔𝐶 𝑗 2 𝜔 2 𝑅 2 𝐶 2
4
+ 𝑗𝜔𝐶𝑅 + 3)
Ora dobbiamo imporre le condizioni di Barkhausen. Il circuito oscilla se la fase del guadagno di
anello è nulla cioè se la parte immaginaria è nulla.
1
3
1
3
+
=
0
→
−
+
=0
𝑗 3 𝑅 2 𝜔 3 𝐶 3 𝑗𝜔𝐶
𝑗𝑅 2 𝜔 3 𝐶 3 𝑗𝜔𝐶
Semplificando:
−
1
𝑅2𝜔 2𝐶 2
+3=0
→
3
3𝑅 2 𝜔2 𝐶 2 = 1
La pulsazione di oscillazione vale:
𝜔0 =
1
√3𝑅𝐶
La frequenza di oscillazione è data da:
1
𝑓0 =
2𝜋√3𝑅𝐶
A questo punto dobbiamo sostituire a ω la pulsazione di oscillazione ricordando che la parte
immaginaria è nulla:
𝛽𝐴 = −
𝑅0
4
− 𝜔2𝐶 2 𝑅
𝑅0 𝜔02 𝐶 2 𝑅
=
=
4
0
Sostituendo a ω0 il valore determinato si trova:
1
𝑅0 3𝑅2 𝐶 2 𝐶 2 𝑅
𝑅0
4
12𝑅
Ricordando le condizioni di Barkhausen le oscillazioni si innescano per βA>1 quindi per:
=
=
𝑅0
> 1 → 𝑅0 > 12𝑅
12𝑅
L’amplificatore operazionale U1 sfasa il segnale presente al nodo A di 180°.
Questo file può essere scaricato gratuitamente. Se pubblicato citare la fonte.
Matilde Consales
4