TIPO1. Analisi e descrizione dell’ algoritmo
Esempio1. Dato in input i secondi dare in output ore, minuti e secondi.
Input 3725
Output: 1h, 2 min, 5 sec
SOLUZIONE:
ANALISI.
Poiché
1h =3600 sec e
1 min= 60 sec,
per trovare ore, min e sec occorre fare
Ore = Sec/3600
Resto = Sec – Ore*3600 (oppure Resto = Sec % 3600)
Min = Resto/60
Sec= Resto – Min*60 (oppure Sec = Resto%60)
Specifiche concettuali.
Dai di input: i secondi
Dati di output: Ore, Min Sec
Modello dei dati.
Nome
variabile
Sec
Tipo di
dato
Intero pos
Ore
Min
Resto
Intero pos
Intero pos
Intero pos
Descrizione
Var di input che memorizza i secondi iniziali e output che
memorizza i secondi residui.
Var di output che contiene le ore
Var di output che contiene i minuti
Var di lavoro che contiene i minuti residui delle ore
SPECIFICHE PER IL TESTING
Nessuna.
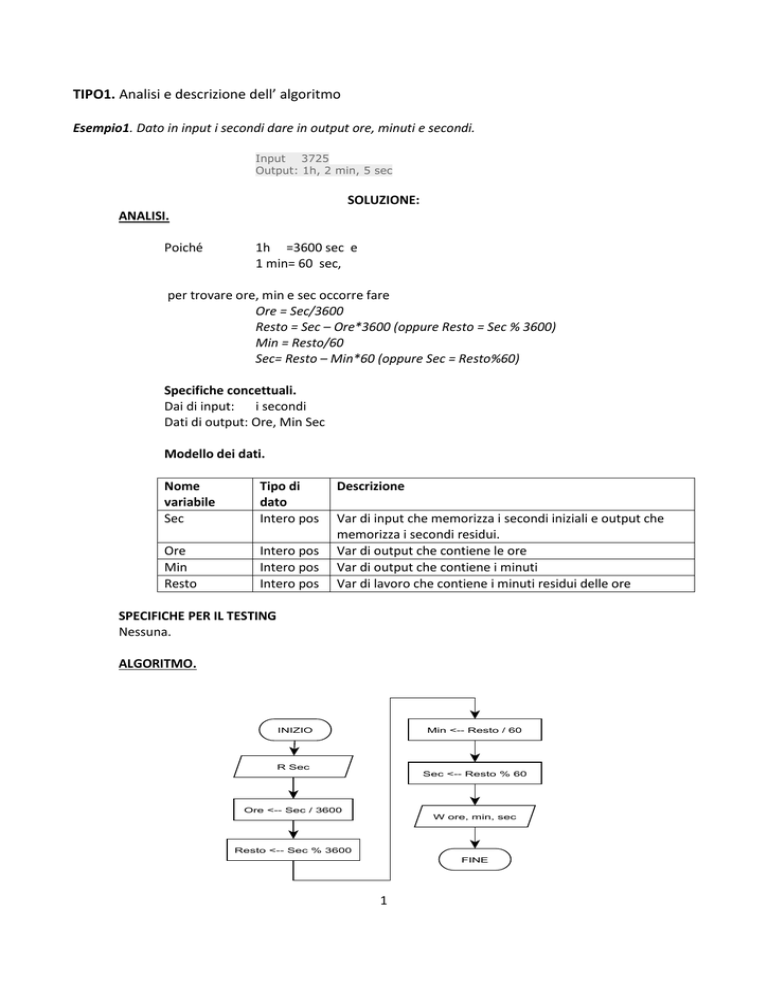
ALGORITMO.
INIZIO
Min <-- Resto / 60
R Sec
Sec <-- Resto % 60
Ore <-- Sec / 3600
W ore, min, sec
Resto <-- Sec % 3600
FINE
1
Esempio2. Un rappresentante può scegliere di essere pagato nei seguenti modi:
a) 0.5 € /km;
b)250 € fissi più il rimborso della benzina.
Conoscendo i chilometri percorsi e sapendo che la sua auto percorre 15 km con un litro di benzina e
che la benzina costa2 € /lt, determinare se gli conviene il pagamento a o b.
Input 600
Output: soluz_a = 300; soluz_b 330; Più conveniente soluz_b: 330
SOLUZIONE1
ANALISI.
Si calcola il rimborso per le due soluzioni e poi si prende il massimo
a) Rimborso_a = 0,5 * KmPercorsi
b) Rimborso_b = 250 + LitriTotali*2, dove LitriTot = KmPercorsi/15
Specifiche concettuali.
Dai di input: KmPercorsi
Dati di output: Rimborso_a, Rimborso_b, Massimo
Modello dei dati.
Nome variabile
KmPercorsi
Rimborso_a
Rimborso_b
Massimo
LitriTot
Tipo di
dato
Intero pos
Reale
Reale
Reale
Reale
Descrizione
Var di input che memorizza i Km percorsi dal rappresentante
Var di output che contiene il rimborso per la soluzione a
Var di output che contiene il rimborso per la soluzione b
Var di output che contiene il rimborso più conveniente
Var di lavoro (opzionale) che contiene i litri consumati
SPECIFICHE PER IL TESTING. Nessuna.
2
ALGORITMO.
INIZIO
R KmPercorsi
Rimborso_a <-- 0,5 * KmPercorsi
LitriTot <-- KmPercorsi / 15
Rimborso_b <-- 250,00 + LitriTot * 2,00
W Rimborso_a, Rimborso_b
massimo <-- Rimborso_b
falso
Rimborso_a
>
Rimborso_b
W "Più conveniente b"
massimo <-- Rimborso_a
vero
W "Più conveniente a"
W massimo
FINE
3
SOLUZIONE2 (Uso di costanti)
Nella soluzione degli esercizi si preferisce sempre utilizzare nomi invece che numeri. Lì dove ci sono delle
quantità numeriche fisse si usa un nome identificatore simbolico (un nome) invece del numero stesso.
Chiamiamo questi identificatori COSTANTI e li definiamo nella tabella dei dati (Vedi tabella dei dati
successiva). Successivamente nel flow chart uso i nomi invece dei numeri. Il diagramma risulta più
comprensibile.
ANALISI.
Si calcola il rimborso per le due soluzioni e poi si prende il massimo
a) Rimborso_a = 0,5 * KmPercorsi
b) Rimborso_b = 250 + LitriTotali* 2 ,
dove LitriTot = KmPercorsi/15
Ricorda di andare a sostituire ogni numero con una costante
Specifiche concettuali.
Dai di input: KmPercorsi
Dati di output: Rimborso_a, Rimborso_b, Massimo
Modello dei dati.
Nome variabile
Rimborso_a
Tipo di
dato
Intero
pos
Reale
Rimborso_b
Reale
Massimo
Reale
LitriTot
Reale
RIMBORSO_AL_KM
KM_CON_UN_LT
FISSO
COSTO_AL_LT
Intero
Intero
Intero
Reale
KmPercorsi
Cost (val) Descrizione
/ Var
Var
Var di input che memorizza i Km percorsi dal
rappresentante
Var
Var di output che contiene il rimborso per la
soluzione a
Var
Var di output che contiene il rimborso per la
soluzione b
Var
Var di output che contiene il rimborso più
conveniente
Var
Var di lavoro (opzionale) che contiene i litri
consumati
Cost 0,5
Rimborso per ogni km
Cost 15
Consumo dell’automobile
Cost 250 Rimborso fisso
Cost 2
Costo della benzina al litro
SPECIFICHE PER IL TESTING. Nessuna.
4
ALGORITMO.
INIZIO
R KmPercorsi
Rimborso_a <-- RIMBORSO_AL_KM * KmPercorsi
LitriTot <-- KmPercorsi / KM_CON_UN_LT
Rimborso_b <-- FISSO + LitriTot * COSTO_AL_LT
W Rimborso_a, Rimborso_b
massimo <-- Rimborso_b
falso
Rimborso_a
>
Rimborso_b
W "Più conveniente b"
massimo <-- Rimborso_a
vero
W "Più conveniente a"
W massimo
FINE
5
SOLUZIONE3 (generalizzazione su consumo automobile e costo benzina)
Per rendere più generale l’algoritmo si riformula la traccia per rendere l’algoritmo utilizzabile per un
qualsiasi rappresentante con un qualsiasi auto e costo variabile della benzina. E’ abbastanza ovvio che il
costo della benzina è variabile e anche i rappresentanti abbiano auto diverse.
FORMULAZIONE GENERALE DEL PROBLEMA.
Un rappresentante può scegliere di essere pagato nei seguenti modi:
a) 1.5 € /km
b)100 € fissi più il rimborso della benzina.
Conoscendo i chilometri percorsi, il consumo al litro dell’ auto del rappresentante, e il costo al litro
della benzina, scrivere un algoritmo che determina se è più conveniente il pagamento a o b.
In questa formulazione più generale il costo della benziona e il consumo dell’auto sono dati di input
e non più costanti.
ANALISI.
Si calcola il rimborso per le due soluzioni e poi si prende il massimo
a) Rimborso_a = 1,5 * KmPercorsi
b) Rimborso_b = 100 + LitriTotali*COSTO_AL_LT,
dove LitriTot = KmPercors i /KM_CON_UN_LT
Specifiche concettuali.
Dai di input: KmPercorsi
Dati di output: Rimborso_a, Rimborso_b, Massimo
Modello dei dati.
Nome variabile
Rimborso_a
Tipo di
dato
Intero
pos
Reale
Rimborso_b
Reale
Massimo
Reale
LitriTot
Reale
RIMBORSO_AL_KM
KmConUnLt
FISSO
CostoAlLt
Intero
Intero
Intero
Reale
KmPercorsi
Cost (val) Descrizione
/ Var
Var
Var di input che memorizza i Km percorsi dal
rappresentante
Var
Var di output che contiene il rimborso per la
soluzione a
Var
Var di output che contiene il rimborso per la
soluzione b
Var
Var di output che contiene il rimborso più
conveniente
Var
Var di lavoro (opzionale) che contiene i litri
consumati
Cost 1,5
Rimborso per ogni km
Var
Var di input consumo dell’automobile
Cost 100 Rimborso fisso
var
Var di input costo della benzina al litro
SPECIFICHE PER IL TESTING. Nessuna.
ALGORITMO. Per esercizio.
6
Esempio3. . In un certo giorno dell’anno nella classe 3° Ainf sono presenti 25 allievi su 30. Determinare la
percentuale dei presenti e quella degli assenti.
FORMULAZIONE GENERALE DEL PROBLEMA.
Calcolare la percentuale degli allievi presenti e quella degli assenti in una classe in un certo giorno,
dati il totale degli allievi e il numero degli assenti.
ANALISI.
Occorre eseguire le seguenti operazioni
PercentualePresenti = Presenti/TotaleAllievi * 100
PercentualeAssenti = 100- PercentualePresenti
Specifiche concettuali.
Dai di input: il totale degli allievi ed il numero di presenti
Dati di output: la percentuale di allievi presenti e la percentuale di allievi assenti
Modello dei dati.
Nome variabile
TotaleAllievi
Presenti
PercentualePresenti
PercentualeAssenti
Tipo di
dato
Intero
Intero
Reale
Reale
Descrizione
Var di input che memorizza il totale degli allievi
Var di input che contiene il numero di allievi presenti
Var di output che rappresenta la percentuale degli allievi presenti
Var di output che rappresenta la percentuale degli allievi assenti
SPECIFICHE PER IL TESTING.
Occorre verificare che il numero totale di allievi sia >0. Nel caso il numero di allievi è negativo
ovviamente il programma produrrà un calcolo che non ha senso. Nel caso invece sia uguale a zero il
programma va in errore poiché non posso fare un divisione per zero.
ALGORITMO.
INIZIO
R
TotaleAllievi, Presenti
TotaleAllievi > 0
falso
vero
PercentualePresenti <-- (Presenti/TotaleAllievi) * 100
W
"Errore TotaleAllievi deve essere > 0"
PercentualeAssenti <-- TotaleAllievi - PercentualePresenti
W
PercentualeAssenti, PercentualePresenti
FINE
7
Esempio4. Stampa dei primi n numeri natural parii, con n intero positivo letto da input.
ANALISI.
IL procedimento risolutivo è il seguente: occorre un ciclo iterativo in cui ad ogni passo si esegue una
singola azione: la stampa del numero. L’azione va iterata per n volte. Per contare usiamo un
contatore.
Specifiche concettuali.
Dai di input: n (quanti numeri si vogliono stampare)
Dati di output: stampa di a ( dove a è il numero naturale al passo attuale)
Modello dei dati.
Nome variabile
n
Cont
a
Tipo di
Descrizione
dato
Intero pos Var di input che memorizza quanti numeri stampare
Intero pos Var contatore che memorizza un numero che va avanti in modo
progressivo
Intero pos Var di output , numero naturale da stampare
SPECIFICHE PER IL TESTING. Nessuna
ALGORITMO.
INIZIO
Rn
cont <-- 0
a <-- 0
vero
cont < n
falso
Wa
FINE
a <-- a + 2
cont <-- cont +1
8
Esempio5. Data l’equazione 2x+1= 0 trovare la soluzione.
SOLUZIONE (da completare)
FORMULAZIONE GENERALE DEL PROBLEMA.
Riformula il problema in modo generale, cioè l’algoritmo deve risolvere tutti i problemi di questa classe.
ANALISI.
Descrivi qui il procedimento a parole
Specifiche concettuali.
Descrivi input e output
Modello dei dati.
Descrivi le variabili e le costati che utilizzi nel tuo algoritmo
Nome variabile
Tipo di
dato
Cost (val) Descrizione
/ Var
SPECIFICHE PER IL TESTING.
Occorre indicare qui eventuali verifiche da fare sulle variabili affinché l’algoritmo non produca
risultati errati oppure termini in modo anomalo. Il comportamento dell’algoritmo anche
quando i valori di ingresso sono ‘critici’ o ‘ai limiti’ è fondamentale. L’algoritmo deve in
ogni caso produrre risultati attendibili.
ALGORITMO.
INIZIO
1
R a, b
2
falso
vero
a = 0
5
3
6
x <-- b / a
7
W "La soluzio è: ", x
W " Impossibile"
FINE
9
4
vero
falso
b = 0
W " Indeterminata"
Esempio6. Dati tre numeri interi a, b, c ordinarli in ordine crescente
SOLUZIONE (da completare)
FORMULAZIONE GENERALE DEL PROBLEMA.
Riformula il problema in modo generale, cioè l’algoritmo deve risolvere tutti i problemi di questa classe.
ANALISI.
Descrivi qui il procedimento a parole
Specifiche concettuali.
Descrivi input e output
Modello dei dati.
Descrivi le variabili e le costati che utilizzi nel tuo algoritmo
Nome variabile
Tipo di
dato
Cost (val) Descrizione
/ Var
SPECIFICHE PER IL TESTING.
Occorre indicare qui eventuali verifiche da fare sulle variabili affinché l’algoritmo non produca
risultati errati oppure termini in modo anomalo. Il comportamento dell’algoritmo anche
quando i valori di ingresso sono ‘critici’ o ‘ai limiti’ è fondamentale. L’algoritmo deve in
ogni caso produrre risultati attendibili.
10
ALGORITMO.
INIZIO
1
R a, b, c
2
falso
vero
a<b
3
8
falso
vero
falso
a<c
10
9
falso
4
5
falso
vero
b<c
vero
b<c
vero
W a, b, c
a<c
W b, a, c
7
12
6
11
W c, a, b
W c, b, a
W a, c, b
W b, c, a
FINE
Esercizi Proposti (Tipo1).
1. Trovare le soluzioni di una equazione di secondo grado. L’algoritmo fornisce le seguenti risposte:
“Equazione di primo grado” se il termine di secondo grado è nullo
“Due soluzioni reali e coincidenti uguali a ……” se è un quadrato perfetto
“Due soluzioni reali e distinte x1=……, x2=
” (se il delta è positivo)
“Non ci sono soluzioni reali” (se il delta è negativo)
2.
3.
4.
5.
6.
7.
8.
9.
10.
Ordinare tre numeri interi a, b, c in ordine decrescente
Trovare il massimo tra tre numeri interi
Dati tre lati di un triangolo, dire se è equilatero, isoscele o scaleno.
Scrivere un algoritmo che legge in input una sequenza di numeri interi positivi chiusa dallo zero e
stampa la percentuale dei pari e dei dispari
Scrivere un algoritmo che stampa la tabellina del 9.
Scrivere un algoritmo che stampa le potenze di 2 fino a 210 . (Usare l’operatore ^ nel flow chart)
Scrivere un algoritmo che dato in input un numero intero n, stampa le potenze di 2 fino a 2n.
Dato un numero n, stampare tutti i suoi fattori
Leggere da input una terna di numeri interi positivi a,b, c fino a quando non si ottiene una terna
pitagorica.
11
TIPO2. Tabella di traccia
Esempio1. Calcolo del prodotto di due numeri interi letti da input con il metodo delle somme
successive
INIZIO
1
R a, b
2
p <-- 0
3
cont <-- 0
4
cont < b
cont <-- cont +1
6
p <-- p + a
5
vero
falso
7
W p
FINE
In questo FLOW CHART sono stati aggiunti i numeri dei blocchi in modo da facilitare la stesura
della ‘tavola di traccia’ che è uno strumento grazie al quale si può esaminare il flusso di
elaborazione dell’algoritmo e verificarne la correttezza.
Si tratta di una tabella in cui si indicano nelle colonne i nomi delle variabili (almeno le più
importanti e significative per l’elaborazione) e nelle righe i passi dell’algoritmo che via via si
svolgono partendo da valori di input scelti a piacere; può essere utile inserire anche una
colonna in cui si indica il valore di verità della condizione da cui dipende l’esecuzione
dell’iterazione.
Quando si esegue la tavola di traccia si deve avere l’accortezza di esaminare il comportamento
dell’algoritmo anche quando i valori di ingresso sono ‘critici’ o ‘ai limiti’; nel caso del prodotto
avremo tale situazione per a uguale a zero, b uguale a zero o entrambi uguali a zero.
Vediamo una prima tavola di traccia del nostro algoritmo scegliendo due valori «normali» delle
variabili, ad esempio a=5, b=3:
12
Il valore di output è, correttamente, 15.
Adesso compiliamo la tavola di traccia di uno dei casi critici, ad esempio con a=7 e b=0:
Il valore di output è, correttamente, 0.
Infine vediamo un altro caso abbastanza particolare con a=8 e b=1:
13
TIPO3. Equivalenza tra algoritmi
Dati due algoritmi dire se sono equivalenti.
INIZIO
R a, b, c
1
3
2
falso
(a = 0)
AND
(b = 0)
vero
W " Indeterminata"
4
falso
5
(a = 0)
AND
(b ! = 0)
vero
W " Impossibile"
6
falso
vero
a ! = 0
x <-- b / a
7
W "La soluzio è: ", x
8
FINE
INIZIO
1
R a, b, c
3
2
(a = 0)
AND
(b = 0)
falso
4
falso
6
x <-- b / a
7
W "La soluzio è: ", x
(a = 0)
AND
(b ! = 0)
vero
W " Indeterminata"
5
vero
W " Impossibile"
FINE
14
TIPO4. Programmazione non strutturata
Esempi di programmazione non strutturata
15