Compito di matematica Classe 3A 22 Febbraio 2010 Alunno

Compito di matematica Classe 3A 22 Febbraio 2010 Alunno
Problema 1
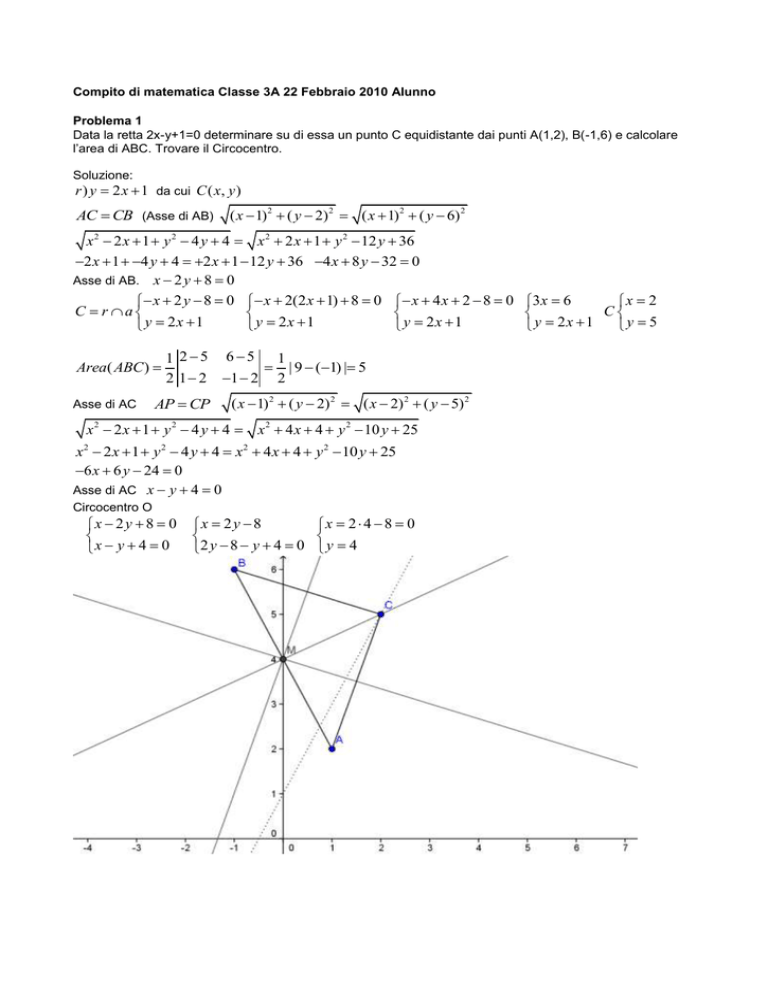
Data la retta 2x-y+1=0 determinare su di essa un punto C equidistante dai punti A(1,2), B(-1,6) e calcolare
l’area di ABC. Trovare il Circocentro.
Soluzione:
r ) y  2 x  1 da cui C ( x, y )
AC  CB (Asse di AB)
( x  1) 2  ( y  2) 2  ( x  1) 2  ( y  6) 2
x 2  2 x  1  y 2  4 y  4  x 2  2 x  1  y 2  12 y  36
2 x  1  4 y  4  2 x  1  12 y  36 4 x  8 y  32  0
Asse di AB. x  2 y  8  0
 x  2 y  8  0  x  2(2 x  1)  8  0  x  4 x  2  8  0 3 x  6
x  2
C  r a
C



 y  2x  1
 y  2x 1
 y  2x 1
 y  2x 1
y  5
Area( ABC ) 
Asse di AC
1 25 65 1
 | 9  (1) | 5
2 1  2 1  2 2
AP  CP
( x  1) 2  ( y  2) 2  ( x  2) 2  ( y  5) 2
x 2  2 x  1  y 2  4 y  4  x 2  4 x  4  y 2  10 y  25
x 2  2 x  1  y 2  4 y  4  x 2  4 x  4  y 2  10 y  25
6 x  6 y  24  0
Asse di AC x  y  4  0
Circocentro O
x  2 y  8  0

x  y  4  0
x  2 y  8
x  2  4  8  0


2 y  8  y  4  0  y  4
Problema 2
Dati due punti A(2,2) B(5,3), determinare sulla retta di equazione 3x-y=6 un punto C tale che l’area del
triangolo ABC misuri 5. Inoltre trovare sul segmento AB un punto D tale che AD=2BD
r )3 x  y  6 da cui C ( x, y ) C ( x,3 x  6)
Area( ABC ) 
1 yC  y A
2 xC  xA
yB  y A 1 3 x  6  2 3  2 1 3 x  8 1 1


 | 9 x  24  x  2 | 5
xB  xA 2 x  2
52 2 x 2 3 2
1
| 8 x  22 | 5 | 8 x  22 | 10
2
1) 8x  22  10 x  4 C (4, 6)
3
3 3
C( ,  )
2) 8x  22  10 x 
2
2 2
D ( x, y ) xD  xA  2( xB  xD ) x  2  2(5  x) x  4
y  2  2(3  y) 3 y  8
yD  y A  2( yB  yD )
Problema 3
In un riferimento cartesiano ortogonale è dato il fascio di rette:
(k-2)x+(1-k)y-3+k=0
a)
b)
c)
d)
e)
trovare il centro del fascio
trovare la retta r del fascio perpendicolare alla retta: x-3y+4=0
trovare la retta s del fascio passante per il punto A(1,4)
trovare la retta t del fascio che ha distanza 1 dal centro degli assi
trovare per quali valori di k il fascio interseca il segmento MN , dove M( -1,5) e N(4,7)
Soluzione:
Punto a)
k=2 (2-2)x+(1-2)y-3+2=0 -y-1=0 y=-1
k=1
(1-2)x+(1-1)y-3+1=0 -x-2=0 x=-2
C(-2,-1)
Punto b)
I metodo sostituendo al fascio di centro C(-2;-1)
retta per pendicolare a x-3y+4=0 : trovo il m=
e quindi la retta è y+1=-3( x  2)
1
3
y=-3x-7
oppure
(k-2)x+(1-k)y-3+k=0
m=-
a
k 2
 3
b
1 k
da cui
5
4
da cui
k  2  3  3k
k
k  2 3(1  k )

1 k
1 k
3 1 7
 x- y- =0 e quindi r: y=-3x-7
4 4 4
Punto c)
Sostituendo A(1,4) ho che (k-2)1+(1-k)4-3+k=0 k-2+4-4k-3+k=0 da cui -2k-1=0 k=-1/2
1
1
1
(- -2)x+(1+ )y-3- =0
2
2
2
5
3 7
- x+ y- =0
2
2 2
-5x+3y-7=0
s; 5x-3y+7=0
Punto d)
(k-2)x+(1-k)y-3+k=0
d=
d=
|(k-2)x+(1-k)y-3+k|
(k  2) 2  (1  k ) 2
=1
|(k-2)(0)+(1-k)(0)-3+k|
(k  2) 2  (1  k ) 2
|-3+k|
k 2  4k  4  k 2  2k  1
|-3+k|
=1
2k 2  6k  5
=1
=1
|-3+k|= 2k 2  6k  5
Quadrando 9-6k+k =2k  6k  5 k  4
2
2
2
k  2
Punto e)
trovo i valori di k in modo che il fascio passa per M( -1,5) e per n N(4,7) (sostituendo)
(k-2)(-1)+(1-k)5-3+k=0
(k-2)(4)+(1-k)7-3+k=0
-k+2+5-5k-3+k=0
4k-8+7-7k-3+k=0
k1 =-
4
5
k 2 =-2
La retta che passa per l’origine ha k=3 e dato che 3 è esterno al segmento e non è compreso tra i due
valori trovati la soluzione è
-2  k  
Problema 4
4
5
Sulle rette di equazione r ) y 
3
3
x
s ) y  3 x  18 , si considerino rispettivamente i punti A e B, di
4
2
ordinata positiva, tali che dette A’ e B’ le rispettive proiezioni sull’asse x, il quadrilatero AA’BB’ risulti un
quadrato. Quali sono le coordinate di A e B?
I modo.
Per costruire il quadrato considero il Punto A su r
E allora
A '  k ;0  e B '  h;0  .
3
 3
A  k ; k   e il punto B su s B  h; 3h  18
2
 4
I punti dovendo avere ordinata positiva abbiamo che
3
3
k   0 k  6 e 3h 18  0 da cui h  6
4
2
E allora per essere un quadrato dobbiamo avere AB=AA’ e AB=BB’
Da cui | h  k ||
3
3
k |
4
2
| h  k || 3h  18 |
Risolviamo prima
3
3

h  k  k 
Il caso in cui h  k 
4
2

h  k  3h  18
A  2;3 B  5;3 A '  2;0  e B '  5;0  .
3
3

h  k  k 
Il caso in cui h  k 
4
2

h  k  3h  18
 4h  7 k  6
k  2

4h  k  18 
0  6k  12 h  5

4h  k  6
h  2

2h  k  18 
6h  12 k  14

A 14;12 B  2;12 A ' 14;0 e B '  2;0  .
II modo
per costruire il quadrato, dato che i punti A e B hanno la stessa y , metto a sistema r ed s con la retta y=k
4k  6
3
3
3
3



4k  3x  6 3x  4k  6  x 
y  x 
k  x 
 4k  6 
A
;k 
A
3
4
2 A 
4
2 


y

k
y

k
3




 y  k
 y  k
 y  k
 k  18

 y  3x  18 k  3x  18  x 
 k  18 
B
;k 
B
3


3


y  k
y  k
 y  k
Da cui
 k  18 
 k  18 
 4k  6 
 4k  6 
A
;k  B
; k  A'
;0  B ' 
;0 
 3

 3

 3

 3

Il quadrato è quella figura che ha i lati uguali. AB=AA’
Da cui |
4k  6  k  18

|| k |
3
3
|
5k  24
|| k | da cui
3
1° soluzione
5k  24
k
3
5k  24  3k k  12 da cui A 14;12 B  2;12 A ' 14;0 e B '  2;0  .
2° soluzione
5k  24
 k
3
5k  24  3k k 
24
 3 da cui A  2;3 B  5;3 A '  2;0  e B '  5;0  .
8
Problema 5
Di un triangolo rettangolo isoscele si sa che il vertice dell’angolo retto è A(2,1) e l’equazione della retta BC è
y=8-2x. Determinare i vertici B e C.
Soluzione.
Per prima cosa trovo l’altezza relativa all’ipotenusa (retta per A e perpendicolare a BC). E il piede
dell’altezza H.
Dato che il coefficiente angolare di BC è m=-2
1
1
( x  2)
y x
2
2
8
1


1
1
1
y
y x







y  x
y  x
y  x
5
2
Da cui H 
H
H
H
H
2
2
2
 1 x  2 x  8
 x  16

 x  4 x  16
5 x  16
 y  2 x  8
 2

5
Altezza AH: y  1 
Ora calcolo la lunghezza dell’altezza AH. (distanza punto retta o distanza AH)
AH 
| 2 xA  y A  8 | 3

4 1
5
In un triangolo rettangolo isoscele BH=CH=AH. e B e C appartengono alla retta y=-2x+8
B, C  x; 2 x  8
Quindi
| x
BH | xB  xH | 1  m 2
16
3
| 5
5
5
|
5 x  16
3
| 5
5
5
5
19
 19 2 
C ; 
5
 5 5
13
 13 14 
B ; 
2) x 
5
5 5
1) x 
BH | x 
16
3
| 1 4 
5
5
| 5 x  16 | 3