Linee di trasmissione

LEZIONI DI ELETTRONICA
per la classe 5° informatica
Prof. Eros Rambelli
10° MODULO : Linee di trasmissione
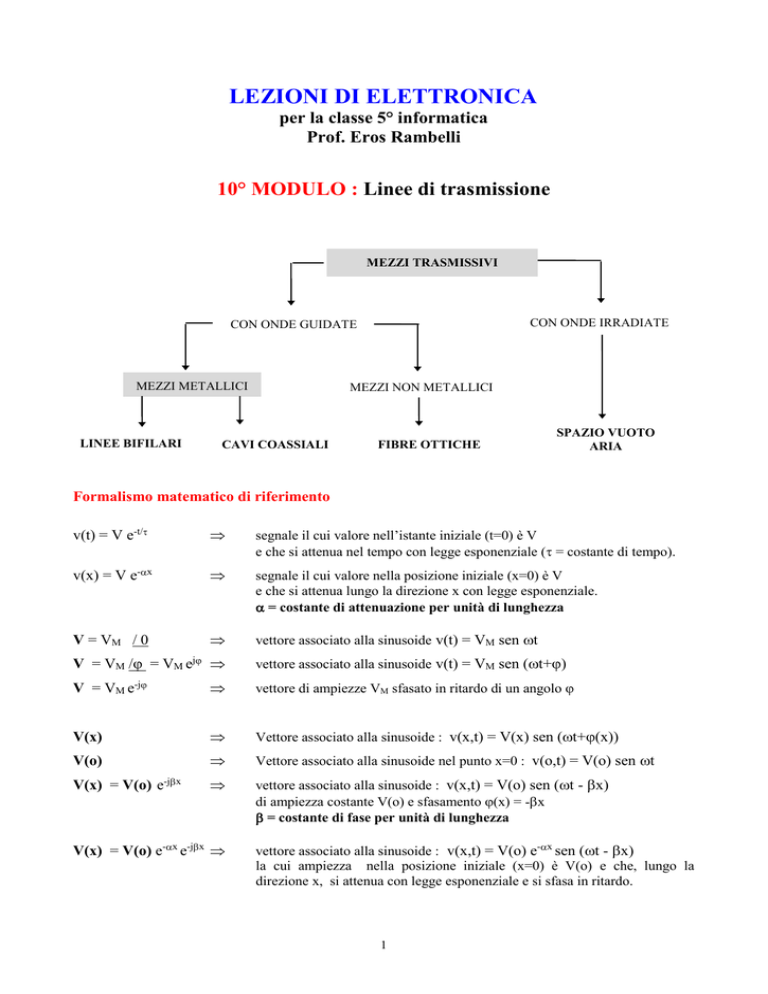
MEZZI TRASMISSIVI
CON ONDE IRRADIATE
CON ONDE GUIDATE
MEZZI METALLICI
LINEE BIFILARI
MEZZI NON METALLICI
CAVI COASSIALI
FIBRE OTTICHE
SPAZIO VUOTO
ARIA
Formalismo matematico di riferimento
v(t) = V e-t/

segnale il cui valore nell’istante iniziale (t=0) è V
e che si attenua nel tempo con legge esponenziale ( = costante di tempo).
v(x) = V e-x

segnale il cui valore nella posizione iniziale (x=0) è V
e che si attenua lungo la direzione x con legge esponenziale.
 = costante di attenuazione per unità di lunghezza
V = VM / 0

vettore associato alla sinusoide v(t) = VM sen t
V = VM / = VM ej 
vettore associato alla sinusoide v(t) = VM sen (t+)
V = VM e-j

vettore di ampiezze VM sfasato in ritardo di un angolo 
V(x)

Vettore associato alla sinusoide : v(x,t) = V(x) sen (t+(x))
V(o)

Vettore associato alla sinusoide nel punto x=0 : v(o,t) = V(o) sen t
V(x) = V(o) e-jx

vettore associato alla sinusoide : v(x,t) = V(o) sen (t - x)
di ampiezza costante V(o) e sfasamento (x) = -x
 = costante di fase per unità di lunghezza
V(x) = V(o) e-x e-jx 
vettore associato alla sinusoide : v(x,t) = V(o) e-x sen (t - x)
la cui ampiezza nella posizione iniziale (x=0) è V(o) e che, lungo la
direzione x, si attenua con legge esponenziale e si sfasa in ritardo.
1
Interconnessioni
Interconnessione : collegamento fisico tra il dispositivo che invia il segnale e il dispositivo che lo riceve
TRASMETTITORE
RICEVITORE
INTERCONNESSIONE
Interconessioni a parametri concentrati : i parametri elettrici (R,C,L) dell’interconnessione si
possono ritenere concentrati in un unico punto.
Un’interconnessione si può rappresentare a parametri concentrati quando il tempo impiegato dall’onda
trasmessa per raggiungere la destinazione è trascurabile rispetto al periodo dell’onda stessa.
Esempio
Rg
Vg
Trasmettitore
Rl
Cl
Vi
interconnessione
Vo
Ro
ricevitore
In questo caso l’analisi del circuito si esegue come se l’interconnessione fosse un semplice quadripolo RC
(filtro passa-basso).
vi(t) = Vi sen t

vo(t) = Vo sen (t-)
Vi = Vi / 0

Vo = Vo e-j
Esercizi
 Determinare i valori di Vo e di 
 Determinare la risposta al gradino
2
Interconessioni a parametri distribuiti : i parametri elettrici (R,C,L,G) dell’interconnessione si
devono considerare distribuiti per tutta la sua lunghezza.
Un’interconnessione si deve considerare a parametri distribuiti se il tempo impiegato dall’onda trasmessa
per raggiungere la destinazione non è trascurabile rispetto al periodo dell’onda stessa.
Le interconessioni di questo tipo prendono il nome di linee.
Vi
Vo
linea
Una linea è costituita da infinite celle infinitesime in cascata tra loro come rappresentato in figura :
I(x)
Ldx
Rdx
I(x)-dI(x)
………….
Cdx
V(x)
Gdx
Ldx
Rdx
………….
Cdx
V(x)-dV(x)
Gdx
………….
..…………
DEFINIZIONE
LINEA DI TRASMISSIONE
Supporto trasmissivo in cui il tempo impiegato dal
segnale per percorrere la distanza L tra trasmettitore
e ricevitore non è trascurabile
COSTANTI PRIMARIE DI UNA LINEA
R
L
C
G
resistenza
per unità
di lunghezza
induttanza
per unità
di lunghezza
capacità
per unità
di lunghezza
conduttanza
per unità
di lunghezza
Per linee bifilari
R=l/S
 = resistività l = lunghezza S = sezione
__
Alle alte frequenze la resistenza cresce a causa dell’effetto pelle : Ro = K d  f
 = permeabilità D = distanza tra i conduttori d = diametro
Alle alte frequenze l’induttanza cresce a causa dell’effetto pelle: L = Li + Le + La
con La = Ro/
L = Li + Le = (/4) + (/) ln2D/d
C =   / ln2D/d
 = costante dielettrica dell’isolante
G
spesso è trascurabile
3
DESCRIZIONE DELLA PROPAGAZIONE DELLE ONDE
NEI MEZZI TRASMISSIVI DI TIPO METALLICO
PROPAGAZIONE DI SEGNALI SINUSOIDALI
 Se applichiamo all’ingresso di un mezzo trasmissivo metallico di lunghezza L una tensione v(t)
sinusoidale, nel mezzo si propaga un’onda con velocità vp .
L’onda raggiunge la destinazione dopo un tempo tp = L/ vp (tempo di propagazione).
 Per effetto della tensione applicata viene inviata nel mezzo trasmissivo anche una corrente i(t)
sinusoidale, che si propaga con la stessa velocità di v(t).
 Attraverso il mezzo trasmissivo viene trasferita energia dal generatore di segnale verso l’utilizzatore.
1. LINEE DI LUNGHEZZA INFINITA
 In una linea di lunghezza infinita l’onda si propaga in modo indefinito.
 In questo caso l’impedenza vista dall’onda sinusoidale è costante in qualunque punto della linea
trasmissiva. Perciò il rapporto vettoriale tra V e I è costante lungo tutto il mezzo trasmissivo.
Questo rapporto, indicato con Zo e denominato “impedenza caratteristica”, dipende dalle caratteristiche
elettriche del mezzo e generalmente anche dalla frequenza dell’onda.
Velocità di propagazione
 La velocità di propagazione vp dipende dalle caratteristiche del mezzo trasmissivo e dalla pulsazione
dell’onda trasmessa.
 Nelle linee a bassa perdita (linee corte) la velocità di propagazione dipende solo dalle proprietà
elettromagnetiche del materiale dielettrico posto tra i conduttori.
Lunghezza d’onda
 Quando in un mezzo trasmissivo viene inviata un’onda sinusoidale, la distanza  percorsa dall’onda in un
periodo viene denominata lunghezza d’onda.
 = vp . T = vp / f
con
vp = velocità di propagazione
4
T = periodo dell’onda
Attenuazione e sfasamento
 Per effetto delle cadute di tensione e delle perdite di corrente che avvengono nel mezzo trasmissivo, le
due onde (tensione e corrente) progressivamente si attenuano e l’energia che si propaga diminuisce.
L’attenuazione è di tipo esponenziale e dipende da un parametro  denominato costante di
attenuazione.
 dipende dalle caratteristiche del mezzo e generalmente anche dalla frequenza.
Se V(0) è l’ampiezza dell’onda all’origine, dopo un tratto x l’ampiezza dell’onda vale V(x) = V(o) e-x
 In un punto x del mezzo trasmissivo l’onda di tensione risulta sfasata in ritardo rispetto a quella di
ingresso di una quantità  (x). La stessa cosa avviene per l’onda di corrente.
Il ritardo di fase introdotto per unità di lunghezza viene indicato con  e denominato costante di fase.
 dipende dalla velocità di propagazione e dalla frequenza dell’onda.
Il ritardo di fase dopo un tratto x vale x.
V(x) = V(o) e-x e-jx
Pertanto il nel punto x vale la seguente relazione :
Come viene vista l’onda da diversi osservatori
 Un osservatore, che guardi da distanza il fenomeno, “vede” un’onda che si propaga con velocità costante.
 Un osservatore fermo all’inizio della linea “vede” un’onda variabile nel tempo in modo sinusoidale di
ampiezza V(o) e pulsazione .
 Un osservatore, che parta con l’onda nel momento in cui questa ha ampiezza massima e si muova alla
stessa velocità dell’onda , “vede” un segnale che cala progressivamente nel tempo in modo esponenziale.
 Un osservatore fermo nella posizione x vede un’onda variabile nel tempo in modo sinusoidale di
pulsazione , ampiezza V(o) e-x e sfasata in ritardo rispetto alla sinusoide di partenza di un angolo x.
5
2. LINEE DI LUNGHEZZA FINITA
- L’onda, che si propaga lungo una linea dal generatore al carico, prende il nome onda diretta o incidente.
- In qualunque punto della linea, l’onda incidente di tensione “vede” davanti a sé la stessa impedenza Zo.
- L’onda incidente di tensione V+ determina un onda incidente di corrente I+ , che in qualsiasi punto della
linea ha lo stesso sfasamento e che si propaga alla stessa velocità.
Se la linea è di lunghezza finita L, quando l’onda arriva alla terminazione “si aspetta” di trovare ancora
un’impedenza pari a Zo. Se ciò non avviene una parte dell’onda si riflette e torna indietro.
Onda riflessa
 Quando l’onda arriva in fondo al mezzo trasmissivo, se l’impedenza ZL del carico è uguale all’impedenza
caratteristica Zo (linea adattata in uscita), l’energia si scarica tutta sul carico e non c’è onda riflessa
 Se invece ZL  Zo una parte dell’energia viene inviata all’indietro. In questo caso si generano onde
riflesse V- e I- (di tensione e di corrente), che si propagano in direzione opposta.
 L’onda riflessa “vede” anch’essa un’impedenza pari a Zo e si propaga con la stessa velocità e con la
stessa legge dell’onda incidente.
 In ogni punto della linea l’onda incidente e quella riflessa si sommano tra loro.
V(x) = V+ e-x e-jx + V- ex ejx
Pertanto il nel punto x vale la seguente relazione :
 Questo fenomeno determina un sottoutilizzo della energia trasmessa da parte dell’utilizzatore.
 Quando l’onda riflessa giunge al punto di inizio della linea, se l’impedenza Zg del generatore di segnale è
diversa da Zo, si ha un nuovo fenomeno di riflessione.
Per evitare ciò occorre adattare la linea anche in ingresso (Zg = Zo).
 Per avere il massimo trasferimento di energia dal generatore all’utilizzatore, le linee trasmissive vanno
adattare sia in ingresso che in uscita.
Coefficiente di riflessione
 Il rapporto tra onda riflessa e onda diretta è indicato con r e denominato coefficiente di riflessione.
Alla terminazione della linea il coefficiente di riflessione vale :
r = V- / V+ = - I- / I+ = (ZL - Zo) / (ZL + Zo)
 Nel caso di linee adattate in uscita (ZL = Zo ) non c’è onda riflessa 
r=0
 Nei casi limiti di linee aperte (ZL = ) o cortocircuitate ZL =0, non potendo il carico assorbire alcuna
energia, l’onda viene riflessa interamente.
Con linee aperte
Con linee cortocircuitate


r = 1  onda riflessa uguale a onda diretta
r = -1  onda riflessa uguale a onda incidente cambiata di segno
6
Onda stazionaria
 Per effetto della sovrapposizione dell’onda incidente e di quella riflessa, all’interno del canale trasmissivo
si forma un’onda stazionaria, che presenta dei massimi quando V+ eV- sono in fase (ventri) e dei minimi
quando V+ e V- sono in opposizione di fase (nodi).
 Anche l’onda di corrente è stazionaria e presenta dei nodi e dei ventri spostati rispetto a quelli di tensione.
Siccome la potenza che attraversa una qualsiasi sezione è costante, dove c’è un ventre di tensione si
forma un nodo di corrente e viceversa
 La distanza tra un nodo e un ventre è di /4. La distanza tra due nodi o tra due ventri è di /2.
 In regime stazionario l’impedenza varia in modo continuo al variare di x, in base alle caratteristiche del
mezzo e a quelle del carico (vedi appendice 1).

Il rapporto tra il modulo della tensione in un ventre e il modulo della tensione in un nodo è denominato
Rapporto di Onda Stazionaria (ROS).
ROS = Vmax/Vmin = Imax/Vmin = (1 +  r ) / (1 - r )
Con linee adattate in uscita 
Con linee aperte

Con linee cortocircuitate

ROS = 0
ROS = 
ROS = 
 sulla terminazione V(L) = V(0) e-L
 sulla terminazione c’è un ventre
 sulla terminazione c’è un nodo
Come viene vista l’onda stazionaria da diversi osservatori
 Per un osservatore, che guardi da distanza il fenomeno, i nodi e i ventri non si muovono.
 Un osservatore fermo su un nodo “vede” un’onda variabile nel tempo in modo sinusoidale di ampiezza
minima (V+ - V-).
 Un osservatore fermo su un ventre “vede” un’onda variabile nel tempo in modo sinusoidale di ampiezza
massima (V+ + V-).
7
TEORIA DELLA PROPAGAZIONE DEI SEGNALI
NELLE LINEE DI TRASMISSIONE
MODELLO A
PARAMETRI DISTRIBUITI CON
CELLE INFINITESIME R-L-C-G
IMPEDENZA
LONGITUDINALE
AMMETTENZA
TRASVERSALE
Zl = R + jL
Yl = G + jC
EQUAZIONI DELLA LINEA
-dV = Zl Idx
-dI = Yl Vdx
caduta di tensione nella cella
perdita di corrente nella cella

d2V / dx2 = Zl Yl V
d2I / dx2 = Zl Yl I
Equazioni dei
telegrafisti
LINEE DI LUNGHEZZA INFINITA
LINEE DI LUNGHEZZA FINITA
Risolvendo le equazioni dei telegrafisti si ottiene :
_____
-x
V(x) = Vo e
con  =  Zl Yl
_____
In questo caso
I(x) = Vo/Zo e-x
Zo =  Zl / Yl
V(x) = V+e-x + V- ex
dove V+ e V- sono costanti complesse che
dipendono dalle condizioni al contorno
(inizio e fine linea).
In questo caso le due componenti
rappresentano rispettivamente
l’onda diretta e l’onda riflessa.
V(x) = Vo e-x e-jx
Il segnale di tensione lungo la linea viene
attenuato esponenzialmente e sfasato in ritardo
La sovrapposizione delle due onde
dà origine ad un’onda stazionaria
Anche per la corrente si ha
un’onda diretta e un’onda riflessa.
Anche la corrente varia in modo analogo
8
Linee di trasmissione : prospetto riepilogativo
COSTANTI PRIMARIE DI UNA LINEA
R
L
C
G
resistenza
per unità
di lunghezza
induttanza
per unità
di lunghezza
capacità
per unità
di lunghezza
conduttanza
per unità
di lunghezza
COSTANTI
SECONDARIE
VELOCITÀ DI PROPAGAZIONE
DI UN’ONDA SINUSOIDALE
o velocità di fase
Zo
vp
impedenza caratteristica
vp = /T = f =  / 2 =  /
Zo = V+ / I+ =V- / I-
nei mezzi metallici
senza perdite
0.6C < U < 0.8C
Nel caso di linee infinite
rappresenta anche
l’impedenza di ingresso
della linea
e ha lo stesso valore
in qualunque punto della linea
con C =3 108 m/s
TEMPO DI PROPAGAZIONE
o ritardo di fase

tp = L/ vp
costante di propagazione
tp = L/ vp = L /  =  /
 =  + j
tp = tempo impiegato dall’onda diretta
per spostarsi dall’inizio della linea
alla terminazione posta ad una distanza D
  costante di attenuazione
  costante di fase
 = sfasamento dell’onda di uscita
rispetto a quella di ingresso
9
PROPAGAZIONE DI SEGNALI NON SINUSOIDALI
Quando il segnale applicato in ingresso al mezzo trasmissivo è composto da più armoniche, ogni armonica
si propaga nel modo sopra descritto e il segnale arriva a destinazione non distorto solo se  è costante (cioè
indipendente dalla frequenza) e  è proporzionale alla frequenza.
In caso contrario ci sarà distorsione di ampiezza e/o di fase.
CONDIZIONI DI NON DISTORSIONE
 indipendente dalla frequenza cioè  = k1
 proporzionale alla frequenza cioè  = k2 

Se  è costante tutte le armoniche vengono attenuate nello stesso modo e pertanto non c’è distorsione di
ampiezza.

Se  è proporzionale a  le armoniche si propagano con la stessa velocità e raggiungono la terminazione
dopo lo stesso tempo tp (tempo di propagazione o ritardo di fase); pertanto non c’è distorsione di fase.
Dimostrazione
 = 2

 = 2 / 

vp = /T = f =  / 2 =  /

tp = L/ vp = L / 

se  = k

tp = Lk
Cioè il tempo di propagazione è indipendente dalla pulsazione.
Se sono verificate le condizioni di non distorsione, il segnale e l’energia si propagano alla stessa velocità
vp detta velocità di fase.
Se non sono verificate le condizioni di non distorsione l’energia si propaga ad una velocità v g diversa da
dalla velocità di fase vp.
Si può dimostrare che vg , denominata velocità di gruppo, vale :
vg = d /d
Di conseguenza il ritardo di gruppo tg (tempo di propagazione dell’energia) vale :
tg = L d/d = d /d
Per ogni mezzo trasmissivo è necessario allora individuare la banda di frequenze per la quale sono verificate
le condizioni di non distorsione e, se possibile, è opportuno operare con frequenze di questo tipo.
10
LINEE CORTE : linee prive di perdite
Nel caso di linee corte la resistenza e la conduttanza della linea sono trascurabili.
Di conseguenza lungo la linea non ci sono perdite di energia.
Valgono le seguenti relazione :
Zl = jL e Yl = jC

_____
Zo =  L / C = Ro  l’impedenza caratteristica è di tipo resistivo
___
____
 = j LC

 = 0 e  =   LC

sono verificate le condizioni di non distorsione
____ ___
vp = 1 /  LC =    la velocità di propagazione non
dipende dalle dimensioni fisiche del canale,
ma solo dalle caratteristiche
elettromagnetiche del materiale dielettrico
tra i conduttori.
0.6C < vp < 0.8C
con C =3 108 m/s
Carico adattato : RL = Ro




Non c’è onda riflessa : regime progressivo.
L’impedenza vista in qualunque punto della linea è Ro.
Corrente e tensione sono in fase in qualunque punto della linea.
Lungo la linea non c’è caduta di tensione : V(x)  = V(o) e I(x) = V(o)/ Ro
Di conseguenza la tensione al carico ha lo stesso modulo di quella all’inizio della linea.
Linea aperta : RL = 








Tutta l’onda diretta si riflette : regime stazionario
Sulla terminazione abbiamo un ventre di tensione e un nodo di corrente : V(L) = 2V(0) e I(L) = 0.
In corrispondenza di tutti nodi l’ampiezza è nulla.
In corrispondenza di tutti ventri di tensione l’ampiezza vale 2V(0).
In corrispondenza di tutti ventri di corrente l’ampiezza vale 2V(0)/Ro.
Siccome la linea non dissipa e il carico non assorbe potenza, non c’è trasmissione di potenza.
Di conseguenza nei vari punti della linea tensione e corrente sono sfasate di /2 o /2 radianti
Dalla parte della terminazione il tratto di linea corrispondente ad un quarto di lunghezza d’onda è di tipo
induttivo; poi, procedendo verso l’inizio della linea, si alternano tratti di tipo capacitivo a tratti di tipo
induttivo, ciascuno di lunghezza pari a un quarto d’onda.
Linea con uscita in corto circuito : RL = 0








Tutta l’onda diretta si riflette : regime stazionario
Sulla terminazione abbiamo un nodo di tensione e un ventre di corrente : V(L) = 0 e I(L) = 2V(0)/Ro.
In corrispondenza di tutti nodi l’ampiezza è nulla.
In corrispondenza di tutti ventri di tensione l’ampiezza vale 2V(0).
In corrispondenza di tutti ventri di corrente l’ampiezza vale 2V(0)/Ro.
Siccome la linea non dissipa e il carico non assorbe potenza, non c’è trasmissione di potenza.
Di conseguenza nei vari punti della linea tensione e corrente sono sfasate di /2 o /2 radianti
Dalla parte della terminazione il tratto di linea corrispondente ad un quarto di lunghezza d’onda è di tipo
capacitivo; poi, procedendo verso l’inizio della linea, si alternano tratti di tipo induttivo a tratti di tipo
capacitivo, ciascuno di lunghezza pari a un quarto d’onda.
11
Propagazione di un gradino nelle linee corte
Rg
Zi=Ro
Vg
Vi
Vo
Linea breve
Vg
4
t
1. Linea adattata in ingresso e in uscita :
Rg = Ro = RL
Vi
2
t
Vo
2
tp
2. Linea aperta adattata in ingresso:
t
Rg = Ro
R L= 
4 Vi
2
tp
2tp
t
Vo
2
tp
t
12
Ro
3. Linea cortocircuitata in uscita e adattata in ingresso:
Rg = Ro
R L= 0
Vi
2
2tp
t
2tp
t
Vo
2
4. Linea adattata in ingresso ma non adattata in uscita :
RL  Ro
Rg = Ro
Coefficiente di riflessione r = (RL – Ro) / (RL + Ro)
Es.
RL = 3Ro
In questo caso r = 1/2
Vi
.
3
2
tp
2tp
t
Vo
.
3
2
tp
t
Esercizi
Disegnare i diagrammi temporali di Vi e Vo nei seguenti casi :

Linea non adattata in ingresso ma adattata in uscita :
Rg = 0.5Ro
RL = Ro

Linea adattata in ingresso ma non adattata in uscita :
Rg = Ro
RL = 1/2 Ro

Linea non adattata in ingresso e non adattata in uscita :
Rg = 0.5Ro
RL = 3Ro
13
Conclusione
Le linee corte hanno un’impedenza caratteristica solo resistiva e non distorcono.
Se
Se
Rg = Ro
RL = Ro


la linea è adattata in ingresso : c’è il massimo di potenza trasmessa
la linea è adattata in uscita : non c’è onda riflessa e la potenza trasferita al
carico è massima.
Le linee lunghe induttive si comportano in modo simile alle linee corte e perciò non distorcono.
Questa condizione si verifica in genere alle frequenze medie, per le quali
 L >>R
 effetto pelle trascurabile.
Le linee lunghe non induttive generano distorsione di ampiezza e di fase.
Questa condizione si verifica in genere alle basse frequenze (L piccolo) e alle alte frequenze (effetto
pelle).
14
APPENDICE :
Approfondimenti sulle linee non adattate
Per analizzare le linee non adattate, conviene indicare la posizione dei vari punti in base alla loro distanza d
della terminazione (d = L-x).
Coefficiente di riflessione lungo una linea non adattata
r(d) = V-(d) / V+(d) = e-2d (ZL – Zo) / (ZL +Zo)
Impedenza lungo una linea non adattata
Z(d) = V(d) / I(d) = Zo (ZL + jZo tg(d)) / (Zo + j ZL tg( d))
Tenuto conto che :
 = 2
/2 = 
/4 = /4
Z(n/2) = ZL  nei punti della linea che distano dalla terminazione un multiplo di /2 l’impedenza vale ZL
Linea chiusa in corto circuito
Z(d) = j Zo tg(d)  in qualsiasi punto della linea l’impedenza è di tipo reattivo.
d=0
0 < d < /4
d = /4
/4 < d < /2
d = /2
/2 < d < 3/4
d = 3/4
3/4 < d < 








impedenza nulla
impedenza induttiva
impedenza infinita
impedenza capacitiva
impedenza nulla
impedenza induttiva
impedenza infinita
impedenza capacitiva
(nodo di tensione, ventre di corrente)
(nodo di corrente, ventre di tensione)
(nodo di tensione, ventre di corrente)
(nodo di corrente, ventre di tensione)
Linea aperta
Z(d) = - j Zo / tg(d)  in qualsiasi punto della linea l’impedenza è di tipo reattivo.
d=0
0 < d < /4
d = /4
/4 < d < /2
d = /2
/2 < d < 3/4
d = 3/4
3/4 < d < 








impedenza infinita
impedenza capacitiva
impedenza nulla
impedenza induttiva
impedenza nulla
impedenza capacitiva
impedenza infinita
impedenza induttiva
(nodo di corrente, ventre di tensione)
(nodo di tensione, ventre di corrente)
(nodo di corrente, ventre di tensione)
(nodo di tensione, ventre di corrente)
15
Adattamento delle linee
Se le linee sono chiuse su un carico diverso da Zo, si possono adattare inserendo prima del carico opportuni
tratti di linea.
Adattamento con linea a quarto d’onda
Si inserisce in cascata alla linea trasmissiva, prima del carico, un tratto di linea di lunghezza /4 avente una
impedenza caratteristica ZA di opportuno valore.
Esempio con carico resistivo
Zo
ZA
RL
/4
Z(/4)
Z(/4) = ZA2 / RL
Se Zo = Z(/4) la linea risulta adattata. Questa condizione è verificata se
____
ZA = Zo RL
Se il carico non è resistivo il tratto aggiuntivo di linea di lunghezza /4 va posto ad una opportuna
distanza (lL) dal carico.
Adattamento con stub
Si inserisce ad una opportuna distanza (lL)dal carico un tratto di linea dello stesso tipo, chiusa in corto
circuito e di lunghezza (lS) calcolabile.
Zo
lS
Zo
Zo
RL
lL
Per ogni tipo di carico, la determinazione del coefficiente di riflessione, del Ros, dell’impedenza in
ogni punto della linea e i calcoli necessari per eseguire l’adattamento (ZA, lL e lS) si possono effettuare
mediante la cosiddetta CARTA DI SMITH, che in questo corso non viene trattata.
16