RISPOSTA IN AMPIEZZA E FASE DI UNA LINEA
Si supponga di esaminare una porzione di linea molto più piccola di un quarto di
lunghezza d’onda e tale quindi da potersi studiare con la teoria delle costanti
concentrate.
Successivamente, estendendo la variazioni a tutta la lunghezza della linea, troveremo
le equazioni di propagazione che esprimeranno l’andamento della tensione Vx e della
corrente Ix lungo tutta la linea.
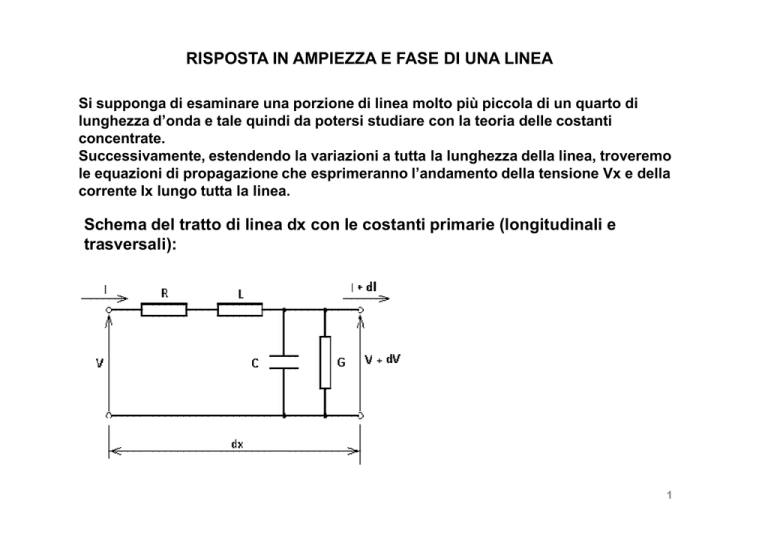
Schema del tratto di linea dx con le costanti primarie (longitudinali e
trasversali):
1
Si supponga che il generatore di segnale sia di tipo sinusoidale e sia x la
distanza della sezione generica della linea dal generatore.
Dall’esame del circuito, applicando i due principi di Kirchhoff, si ha:
e, dividendo membro a membro per dx:
Queste equazioni esprimono il legame esistente fra la tensione, la
corrente, e le loro variazioni, lungo la linea in funzione delle costanti
primarie R, L, G, C, della linea.
2
Le soluzioni delle equazioni dei telefonisti e dei telegrafisti sono:
In cui:
è la costante di propagazione
è l’ impedenza caratteristica
Ambedue, come già visto, prendono il nome di costanti secondarie delle linee.
3
Per comprendere il significato fisico delle soluzioni delle equazioni dei Telefonisti,
occorre esaminare separatamente i termini a secondo membro delle due
espressioni.
Ambedue le relazioni hanno due componenti:
•
la prima ad esponente negativo, con ampiezza decrescente
•
la seconda ad esponente positivo, con ampiezza crescente
La prima componente rappresenta un’onda di tensione ed una di corrente
che, partendo dal generatore, percorrono tutta la linea fino al carico:
ONDA DIRETTA
La seconda componente rappresenta un’onda di tensione ed una di corrente
che, partendo dal carico, percorrono la linea verso il generatore: ONDA
RIFLESSA
4
Onda diretta
V= Vd *
e- x +
Vr * e
I= Id * e- x + Ir * e
x
e- x
Onda riflessa
ex
x
GENERATORE
CARICO
5












