UNIVERSITÀ DEGLI STUDI DI MILANO BICOCCA
FACOLTÀ DI SCIENZE STATISTICHE
Corso di laurea in Scienze Statistiche ed Economiche
Corso in
ECONOMIA DELLE ASSICURAZIONI
Professoressa
Chiara Parrini
[email protected]
Considerazioni generali sulle
imprese di assicurazione (1/2)
L’art. 1882 del Codice Civile definisce il contratto di
assicurazione come “il contratto con il quale l’assicuratore,
verso pagamento di un premio, si obbliga a rivalere
l’assicurato, entro i limiti convenuti, del danno ad esso
prodotto da un sinistro, ovvero a pagare un capitale o una
rendita al verificarsi di un evento attinente alla vita umana”.
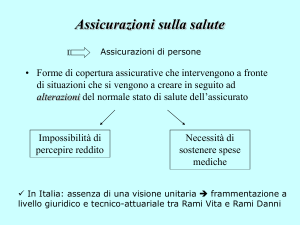
Assicurazioni contro i danni
Assicurazioni sulla vita
Considerazioni generali sulle
imprese di assicurazione (2/2)
Assicurazioni contro i danni
Assicurazioni sulla vita
- Le prestazioni sono prevalentemente - Le prestazioni sono importi prefissati
a carattere risarcitorio
(o comunque determinabili in modo prefissato)
- Breve durata contrattuale
- Medio/lunga durata contrattuale
(in genere un anno)
- Ripetibilità dell’evento dannoso
(ad esempio alcune fanno riferimento all’intera
durata residua della vita umana)
- Non ripetibilità dell’evento
Le assicurazioni contro i danni (1/2)
CLASSIFICAZIONE
Con riferimento alle coperture che
prevedono una prestazione avente carattere di risarcimento
assicurazioni di danni
a beni di proprietà
assicurazioni di
responsabilità civile
(ad esempio rischio credito,
furto, incendio e trasporti )
(ad esempio l’assicurazione
di responsabilità civile autoveicoli)
Le assicurazioni contro i danni (2/2)
CLASSIFICAZIONE
Nelle assicurazioni contro i danni si collocano inoltre
alcune coperture riguardanti i danni alla persona
Rischio infurtunio
Rischio malattia
Le assicurazioni contro i danni alla persona
possono non avere carattere di risarcimento e prevedere,
analogamente alle assicurazioni sulla vita,
una prestazione di importo prefissato
in conseguenza di un infortunio o di una malattia.
Rami Danni in Italia
(decreto legislativo 17 marzo 1995, n. 175)
(1) infortuni (compresi infortuni sul lavoro e malattie professionali);
(2) malattia;
(3) corpi di veicoli terrestri (esclusi quelli ferroviari);
(4) corpi di veicoli ferroviari;
(5) corpi di veicoli aerei;
(6) corpi di veicoli marittimi, lacustri e fluviali;
(7) merci trasportate (compresi merci, bagagli ed ogni altro bene);
(8) incendio ed elementi naturali (in particolare, i danni causati da un incendio, da un’esplosione
e da una tempesta);
(9) altri danni ai beni (in particolare, i danni causati dalla grandine, dal gelo e dal furto);
(10) responsabilità civile autoveicoli terrestri;
(11) responsabilità civile aeromobili;
(12) responsabilità civile veicoli marittimi, lacustri e fluviali;
(13) responsabilità civile generale;
(14) credito (compresi credito all’esportazione, vendite a rate, credito agricolo e perdite
patrimoniali derivanti da insolvenze);
(15) cauzione (diretta o indiretta);
(16) perdite pecuniarie di vario genere (in particolare, i rischi relativi all’occupazione e la
perdita di fitti o di redditi);
(17) tutela giudiziaria;
(18) assistenza.
Le assicurazioni sulla durata vita
•
Contratto mediante il quale l’assicurato versa, anticipatamente, uno o più
premi, affinché la Compagnia di Assicurazione si impegni a pagare uno o
più capitali, al verificarsi di eventi legati alla sopravvivenza o alla
premorienza di un individuo o gruppo di individui.
•
Nella polizza si individuano:
– Assicuratore: impresa (autorizzata) che si impegna ad erogare il
capitale assicurato al verificarsi dell’evento/i considerati,
– Contraente: soggetto che stipula il contratto e paga il premio,
– Assicurato/i: testa/e a cui si riferiscono gli eventi assicurati,
– Beneficiario: soggetto a cui verranno pagate le somme assicurate.
Le assicurazioni sulla durata vita
CLASSIFICAZIONE DEI CONTRATTI
Una prima classificazione di base è prevista dal decreto legislativo 174 del
1995 il quale classifica i contratti in 6 rami:
•
I - Le assicurazioni sulla durata della vita umana.
•
II - Le assicurazioni di nuzialità, le assicurazioni di natalità.
•
III - Le assicurazioni di cui ai punti I e II connesse con fondi di investimento.
•
IV - L'assicurazione malattia di cui all'art. 1, numero 1, lettera d), della
direttiva CEE n. 79/267 del 5 marzo 1979.
•
V - Le operazioni di capitalizzazione di cui all'art. 40 del presente decreto.
•
VI - Le operazioni di gestione di fondi collettivi costituiti per l'erogazione di
prestazioni in caso di morte, in caso di vita o in caso di cessazione o riduzione
dell'attività lavorativa.
Le assicurazioni sulla durata vita
I TIPI DI POLIZZA
•
Polizze TRADIZIONALI:
Prestazioni e premi monetariamente predeterminati (livelli costanti o
variabili in modo prefissato) alla stipulazione del contratto.
•
Polizze FLESSIBILI:
non c’è predeterminazione monetaria degli importi assicurati, si
fissano delle regole di determinazione degli stessi.
Le assicurazioni sulla durata vita
LE POLIZZE TRADIZIONALI
•
•
•
•
Assicurazione di capitale in caso di vita:
• Capitale differito
Rendite in caso di vita:
• Rendita vitalizia:
– Anticipata/posticipata
– Temporanea
– Differita
– Frazionata
– Con rate in progressione aritmetica
Assicurazioni di capitale in caso di morte:
• Assicurazione a vita intera
• Assicurazione temporanea e differita
• Assicurazione di annualità
Assicurazioni miste:
• Mista semplice
• Mista doppia
• Mista a capitale raddoppiato
• Semi-mista
Le assicurazioni sulla durata vita
LE POLIZZE FLESSIBILI (1/3)
¾ Tipi di flessibilità nelle prestazioni
•
Connessione ad indicatori economico-finanziari “interni” o “esterni”
alla Compagnia:
• Rendimento delle investimenti collegati alle riserve
matematiche,
• Inflazione,
• Indici di borsa.
•
Opportunità fornita al contraente di variare le condizioni contrattuali:
• Livello dei premi,
• Sospensione del pagamento dei premi,
• Eventuali prelevamenti di quote della riserva matematica.
Le assicurazioni sulla durata vita
LE POLIZZE FLESSIBILI (2/3)
¾ MOTIVAZIONI
•
•
•
•
Inflazione
Rendimento investimenti/tasso tecnico
Partecipazione degli assicurati all’utile della Compagnia
Concorrenza sul mercato finanziario
¾ ALCUNI ESEMPI
Assicurazioni
indicizzate:
Assicurazioni
rivalutabili:
Garantisce la protezione totale
del potere d’acquisto
delle somme assicurate
Viene retrocesso agli
assicurati parte dell’utile finanziario
della Compagnia
dietro adeguamento del premio
Le assicurazioni sulla durata vita
LE POLIZZE FLESSIBILI (3/3)
¾ UNIT e INDEX LINKED
•
Forme assicurative caratterizzate da una diretta dipendenza dalle
prestazioni al valore di un fondo o di un indice azionario o altro valore di
riferimento.
POLIZZA
UNIT-LINKED
POLIZZA
INDEX-LINKED
Le assicurazioni contro i danni
Condizioni Contrattuali di Copertura (1/4)
Assicurazioni di danni a beni di proprietà
V: massimo danno possibile,
possibile distribuzione totale del bene.
V°: valore del bene all’epoca di stipulazione del contratto.
>
V = V°
<
L: massimo danno probabile (“maximum probable loss”)
estremo superiore degli importi ai quali viene soggettivamente
attribuita una probabilità positiva di verificarsi.
L≤V
Le assicurazioni contro i danni
Condizioni Contrattuali di Copertura (2/4)
Assicurazioni di danni a beni di proprietà
Copertura totale
l’assicurato decide di assicurare il
bene per l’intero valore, V°
la scelta è fatta dall’assicurato in base
allo stato di informazione a sua disposizione
all’epoca di stipulazione del contratto
Copertura parziale
l’assicurato decide di assicurare il
bene per un valore, V', inferiore
all’intero valore
ad esempio
il massimo
danno probabile
Sottoassicurazione
Le assicurazioni contro i danni
Condizioni Contrattuali di Copertura (3/4)
Assicurazioni di responsabilità civile
Non essendo specificato un bene di riferimento, non risulta individuabile
un valore in grado di rappresentare il massimo danno possibile……
1) assicurazione a garanzia illimitata
risarcimento del danno
senza alcuna limitazione
Copertura totale
del rischio
2) assicurazione con massimale di garanzia
risarcimento del danno stabilito
nei limiti di un importo, M,
prefissato, denominato
massimale di garanzia
Copertura parziale
del rischio
Le assicurazioni contro i danni
Condizioni Contrattuali di Copertura (4/4)
Assicurazioni di responsabilità civile
L’introduzione del massimale di garanzia
(eventualmente posto eguale al massimo danno probabile)
si prefigge di contenere,
contenere entro un limite ragionevole,
l’esposizione monetaria al rischio dell’assicuratore.
Obiettivo importante per il rapporto assicurativo,
in assenza di un valore rappresentativo
del massimo danno possibile.
Le assicurazioni contro i danni
Clausole Contrattuali di Copertura
FRANCHIGIA (1/2)
Clausola frequentemente utilizzata sia nelle assicurazioni di danni a beni di
proprietà che nelle assicurazioni di responsabilità civile
• Franchigia di valore
di importo f
i danni di importo non superiore a f non vengano risarciti,
mentre i danni di importo superiore a f, vengano risarciti:
Parzialmente,
per l’eccedenza rispetto ad f,
FRANCHIGIA ASSOLUTA
Integralmente,
FRANCHIGIA RELATIVA
Le assicurazioni contro i danni
Clausole Contrattuali di Copertura
FRANCHIGIA (2/2)
• Franchigia di valore
Nell’assicurazione di danni a beni di proprietà, risulta frequente
esprimere la franchigia in percentuale del valore del bene assicurato
(soprattutto nelle assicurazioni contro il rischio di incendio
e nelle assicurazioni delle merci trasportate).
• Franchigia temporale
generalmente espressa in numero di giorni
Una franchigia di durata t (giorni) indica il fissato numero di giorni,
giorni
a partire dalla data di accadimento del sinistro,
durante i quali la garanzia non è operante.
operante
(assicurazioni contro il rischio di incendio, assicurazioni dei danni
indiretti da guasti alle macchine, assicurazioni sulla salute)
Le assicurazioni contro i danni
Clausole Contrattuali di Copertura
SCOPERTO
Clausola utilizzata soprattutto nelle coperture contro il rischio
di insolvenza dei crediti commerciali
Viene fissata un’aliquota ξ (0 < ξ < 1) del rischio
(quindi del risarcimento relativo ad un sinistro)
posta a carico dell’assicurato
OSSERVAZIONE:
In un’assicurazione di danni a beni di proprietà, la clausola di scoperto
corrisponde formalmente ad una copertura assicurativa a valore parziale.
In questo caso, però,
però la situazione di sottoassicurazione
deriva da una decisione dell’assicuratore
e non da una scelta dell’assicurato
Le assicurazioni contro i danni
Clausole Contrattuali di Copertura
OBIETTIVI
1. L’obiettivo prioritario è ridurre il valore atteso dei risarcimenti
2. La franchigia, eliminando i piccoli sinistri (“small claims”),
generalmente numerosi, è in grado di realizzare una riduzione
delle spese di gestione connesse alla liquidazione dei sinistri
Sostanzialmente le clausole contrattuali producono una
(talvolta rilevante)
diminuzione del prezzo della copertura assicurativa
Le assicurazioni contro i danni
Clausole Contrattuali di Copertura
EFFETTO PSICOLOGICO
Le clausole contrattuali corresponsabilizzano l’assicurato
sollecitandolo ad adottare tutte le precauzioni possibili
ai fini della prevenzione dei sinistri
riducono il Fenomeno del “Moral Hazard”
rischio, per l’assicuratore, di un aumento della sinistrosità
derivante da un imprudente comportamento dell’assicurato.
Le assicurazioni contro i danni
ULTERIORI CLAUSOLE CONTRATTUALI
Assicurazioni sulla salute:
rischio infortunio e rischio malattia
a) Periodo di carenza iniziale (“waiting period”)
arco di tempo,
tempo
susseguente la stipula del contratto,
che esclude dalla copertura assicurativa
le malattie che in esso si manifestano
Contiene i costi e contrasta,
contrasta
almeno parzialmente,
gli effetti del fenomeno
di “antiselezione”
antiselezione
b) Periodo di qualificazione (in genere breve: qualche settimana)
arco di tempo,
tempo
a partire dal verificarsi della malattia o
dall’insorgere dell’incapacità lavorativa,
necessario affinché l’assicurato sia
titolato a percepire il beneficio
Tale periodo opera come
“franchigia relativa”.
Può essere incluso
nel periodo di franchigia
(rendite o diarie)
LE ASSICURAZIONI
CONTRO I DANNI
La base tecnica del rischio
Sinistri, danni e risarcimenti (1/2)
Nel periodo di copertura, in genere un anno, il contratto di
assicurazione è colpito da un numero aleatorio, N, di sinistri.
Ciascun sinistro determina un danno di importo aleatorio.
aleatorio
Sia Zi il danno derivante dall’i-esimo (i=1,2,…) sinistro
in ordine cronologico.
N: variabile aleatoria che rappresenta il numero di sinistri,
le cui possibili determinazioni sono i numeri naturali
Zi: variabile aleatoria che rappresenta il danno relativo all’i-esimo sinistro,
sinistro
le cui possibili determinazioni sono i numeri reali
Sinistri, danni e risarcimenti (2/2)
In corrispondenza del danno Zi l’assicuratore effettua,
a beneficio dell’assicurato,
il pagamento dell’importo aleatorio Yi ,
denominato risarcimento.
• Relazione tra il Danno ed il Risarcimento
Yi = ϕ ( Z i )
Funzione di risarcimento:
rappresentativa delle condizioni contrattuali di copertura
(ovviamente 0 ≤ Yi ≤ Zi )
Funzione di risarcimento (1/6)
ESEMPIO (1/6)
Y=Z
Funzione di risarcimento rappresentativa di una copertura
che garantisce il risarcimento dell’intero importo
del danno determinato da un sinistro
¾ copertura a valore intero, nel caso di un’assicurazione di
danni a beni di proprietà
¾ copertura a garanzia illimitata, nel caso di un’assicurazione
di responsabilità civile
Funzione di risarcimento (2/6)
ESEMPIO (2/6)
⎧Z
Y=⎨
⎩M
se Z ≤ M
o,
Y
=
min
(
Z
,
M
)
,
se Z > M equivalente mente
Funzione di risarcimento rappresentativa di una copertura
che garantisce il risarcimento del danno
nei limiti di un importo prefissato M
¾ copertura a primo rischio assoluto, nel caso di
un’assicurazione di danni a beni di proprietà
¾ copertura con massimale di garanzia, nel caso di
un’assicurazione di responsabilità civile
Funzione di risarcimento (3/6)
ESEMPIO (3/6)
⎧ 0
Y=⎨
⎩Z − f
se Z ≤ f
se Z > f
o, anche
Y = max (0, Z − f ) ,
¾ Funzione di risarcimento rappresentativa,
sia nel caso di un’assicurazione di danni a beni di proprietà
sia nel caso di un’assicurazione di responsabilità civile,
di una copertura con franchigia assoluta (di importo f).
Funzione di risarcimento (4/6)
ESEMPIO (4/6)
⎧0
Y=⎨
⎩Z
se Z ≤ f
se Z > f
¾ Funzione di risarcimento rappresentativa,
sia nel caso di un’assicurazione di danni a beni di proprietà
sia nel caso di un’assicurazione di responsabilità civile,
di una copertura con franchigia relativa (di importo f).
Funzione di risarcimento (5/6)
ESEMPIO (5/6)
⎧ 0
⎪
Y = ⎨Z−f
⎪M − f
⎩
se Z ≤ f
se f < Z ≤ M
se Z > M
o,
Y = min [ max (0, Z − f ) , M − f ] ,
Funzione di risarcimento rappresentativa di una copertura che,
in presenza di una franchigia assoluta (di importo f),
garantisce il risarcimento del danno nei limiti
di un importo prefissato M
¾ copertura a primo rischio assoluto con franchigia assoluta,
nel caso di un’assicurazione di danni a beni di proprietà
¾ copertura con massimale di garanzia e franchigia assoluta,
nel caso di un’assicurazione di responsabilità civile.
Funzione di risarcimento (6/6)
ESEMPIO (6/6)
Y = (1 − ξ) Z ,
con 0 < ξ < 1
¾ Funzione di risarcimento rappresentativa,
sia nel caso di un’assicurazione di danni a beni di proprietà
sia nel caso di un’assicurazione di responsabilità civile,
di una copertura con scoperto (di aliquota ξ).
Il risarcimento globale
0
⎧
X=⎨
⎩Y1 + Y2 + ⋅ ⋅ ⋅ + YN
se N = 0
se N ≥ 1
o, anche,
X=
N
∑ Yi ,
i=0
dove Y0 è l’importo certo nullo.
X: variabile aleatoria che rappresenta il risarcimento globale,
le cui possibili determinazioni sono i numeri reali non negativi.
9 NOTA: Si evidenzia che è trascurata la componente finanziaria relativa
alla diversa collocazione temporale dei sinistri e dei conseguenti risarcimenti
posti a carico dell’assicuratore.
Ciò si giustifica con l’usuale brevità del periodo di copertura.
copertura
La Base Tecnica del Rischio (1/7)
IPOTESI (1/3)
Si consideri un portafoglio di contratti di assicurazione
riferiti ad un medesimo tipo di rischio
IPOTESI:
IPOTESI
1. I contratti siano tutti contemporaneamente stipulati
2.
I contratti siano contraddistinti da un eguale periodo di copertura
3.
Il portafoglio sia composto da rischi analoghi,
analoghi con riferimento:
1) alle caratteristiche del rischio adeguatamente valutabili,
all’epoca di stipulazione del contratto, da parte dell’assicuratore;
2) alle condizioni contrattuali di copertura
3) ai valori monetari di esposizione al rischio
(ad esempio i valori dei beni assicurati o i massimali di garanzia)
La Base Tecnica del Rischio (2/7)
IPOTESI (2/3)
In tali ipotesi i rischi del portafoglio sono tra loro :
-qualitativamente e quantitativamente omogenei rispetto ai suddetti
elementi ;
-eterogenei rispetto ad eventuali caratteristiche non adeguatamente
valutabili all’epoca di stipulazione del contratto
(ad esempio, nell’assicurazione di responsabilità civile autoveicoli:
il comportamento alla guida, la conoscenza del codice, i chilometri annui percorsi,…..)
La Base Tecnica del Rischio (3/7)
IPOTESI (3/3)
Si scelga a caso un rischio nel portafoglio e sia
X=
N
∑ Yi ,
i=0
il risarcimento globale a carico dell'assicuratore, con Yi = φ(Zi).
ULTERIORI IPOTESI (semplificatrici della realtà):
1. il numero di sinistri, N, e il danno Zi (e quindi, il risarcimento Yi)
relativo all’i-esimo (i=0,1,…; Z0≡0) sinistro, in ordine cronologico,
siano tra loro indipendenti;
2.
per ogni determinazione k (k ≠ 0) della v.a. N, i danni Z1, Z2, …, Zk
(e quindi, i risarcimenti Y1,Y2,…,Yk) siano tra loro indipendenti ed
identicamente distribuiti
La Base Tecnica del Rischio (4/7)
FUNZIONE DI RIPARTIZIONE DEL
RISARCIMENTO GLOBALE
Indicato con:
- FZ (rispettivamente, FY) la funzione di ripartizione del danno Z
(rispettivamente, del risarcimento Y)
- FN la funzione di ripartizione del numero di sinistri N
funzione di ripartizione del risarcimento globale
+∞
FX ( x ) = ∑ pk FYk * ( x ) ,
per ogni x ≥ 0
k =0
pk = Pr{N = k}
⎧k
⎫
F ( x ) = Pr ⎨∑ Yi ≤ x ⎬
⎩ i =0
⎭
k*
Y
La Base Tecnica del Rischio (5/7)
CONVOLUZIONE
• Convoluzione k-esima di FY
k
⎧
⎫
FYk * ( x ) = Pr ⎨∑ Yi ≤ x ⎬ ,
⎩ i =0
⎭
con FY0* = 1 per ogni x ≥ 0
è la funzione di ripartizione della somma di k importi aleatori
non negativi, indipendenti e identicamente distribuiti
La Base Tecnica del Rischio (6/7)
La Base Tecnica del Rischio
è la distribuzione di probabilità del risarcimento globale X
Le distribuzioni di probabilità del numero di sinistri N
e del danno Z costituiscono la base tecnica del rischio.
La Base Tecnica del Rischio (7/7)
FUNZIONE DI RIPARTIZIONE DEL RISARCIMENTO
In forza della relazione esistente tra danno e risarcimento,
la funzione di ripartizione FY (quindi, la FYk* per k ≥ 1)
è costruita a partire:
dalla funzione di ripartizione
del danno, FZ
dalla funzione
di risarcimento, φ
LE ASSICURAZIONI
CONTRO I DANNI
I modelli probabilistici
per le variabili aleatorie
La distribuzione di probabilità
del numero di sinistri
N: variabile aleatoria che rappresenta il numero di sinistri,
le cui possibili determinazioni sono i numeri naturali
Individuare i modelli probabilistici più adeguati per
descrivere la distribuzione di probabilità
del numero di sinistri N
N è rappresentata da una distribuzione di probabilità discreta
{k, pk ; k = 0,1,2,…}
possibili determinazioni
probabilità
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
Modelli più frequentemente adottati
(1) distribuzione di Poisson;
(2) distribuzione di Poisson doppia;
(3) distribuzione mistura finita di Poisson;
(4) distribuzione binomiale negativa;
(5) distribuzione mistura di Poisson:
a) modello Poisson-gamma
b) modello Poisson-gaussiana inversa
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione di Poisson di parametro positivo λ
pk = e − λ
λk
k!
Propensione al sinistro:
numero atteso di sinistri che
colpiscono il rischio nel
periodo di copertura
PROPRIETÀ della distribuzione di Poisson
la distribuzione di Poisson soddisfa la formula ricorrente
⎛λ ⎞
pk = ⎜ ⎟ pk −1 ,
⎝k⎠
k = 1, 2, ... ,
con p0 = e-λ
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
INCONVENIENTE della distribuzione di Poisson
E(N) = var(N) = λ
Mentre le usuali evidenze empiriche mostrano varianza
più elevata del valor medio
DISTRIBUZIONE DI POISSON DOPPIA
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione di Poisson doppia
di parametri positivi ε, λ1 e λ2 , con 0 < ε < 1
⎛ − λ λk2 ⎞
⎛ − λ λk1 ⎞
⎟ .
⎟ + (1 − ε) ⎜ e 2
p k = ε ⎜⎜ e 1
⎟
⎜
⎟
k
!
k
!
⎠
⎝
⎠
⎝
Combinazione lineare di 2 variabili di Poisson
PROPRIETÀ: Valore atteso e Varianza
E(N) = ε λ1 + (1-ε) λ2
var(N) = ε λ1 + (1-ε) λ2 + ε (1-ε) (λ1 + λ2)2
E(N)
Componente positiva
che fa risultare la varianza
superiore alla media
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
La distribuzione di Poisson doppia è adatta a rappresentare
il numero di sinistri nell’ipotesi che il portafoglio sia costituito
da rischi caratterizzati da 2 diverse propensione al sinistro
ESEMPIO
Portafoglio costituito:
- da una percentuale ε di rischi “buoni”
(vale a dire, con propensione al sinistro λ1)
- da una percentuale 1-ε di rischi “cattivi”
(con propensione al sinistro λ2, essendo λ2 > λ1).
Dove la differenza tra i primi ed i secondi è dovuta ad alcune caratteristiche del
rischio non adeguatamente valutabili all’epoca
di stipulazione dei contratti.
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione mistura finita di Poisson
di parametri positivi εj e λj (j=1,2,…,m), con ∑ j ε j = 1.
Generalizziamo il ragionamento precedente considerando una “mistura”
di m distribuzioni poissoniane,
poissoniane con m numero intero non inferiore a due
⎛ −λ1 λ1k ⎞
⎟⎟ + ... + ε m
pk = ε1 ⎜⎜ e
k! ⎠
⎝
⎛ −λm λkm ⎞
⎜⎜ e
⎟⎟
k! ⎠
⎝
MEDIA E VARIANZA
m
E( N) = ∑ ε j λ j
j=1
;
⎛
⎞⎛
⎞
⎜
⎟
⎜
var(N) = ∑ ε j λ j + ∏ ε j ∑ λ j ⎟
⎜ j=1 ⎟ ⎜ j=1 ⎟
j=1
⎠
⎝
⎠⎝
m
m
m
2
Componente aggiuntiva
.
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione Binomiale Negativa
di parametri positivi r e q, con 0 < q < 1
⎛ r + k − 1⎞ r
p k = ⎜⎜
⎟⎟ q (1 − q) k ,
⎝ k ⎠
⎛ r + k − 1⎞ (r ) k
⎟⎟ =
, con (r)k = r(r+1)…(r+k-1) e, in particolare, (r)0 = 1
k!
⎝ k ⎠
dove è ⎜⎜
PROPRIETÀ della distribuzione di Poisson
la distribuzione Binomiale Negativa soddisfa la formula ricorrente
⎡ (1 − q )(r + k − 1) ⎤
p k −1 ,
pk = ⎢
⎥
k
⎦
⎣
k = 1, 2, ... ,
con p0 = qr
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione Binomiale Negativa
MEDIA E VARIANZA
r (1 − q)
E( N) =
,
q
var( N) =
var(N) > E(N)
(Ricordiamo che 0 < q < 1)
r (1 − q )
q
2
.
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione mistura di Poisson di parametro
aleatorio positivo Λ
pk =
+∞
∫
p k (λ) dFΛ (λ ) ,
0
p k (λ ) = Pr{N = k | Λ = λ} = e − λ
k
λ
,
k!
Funzione peso (della mistura)
funzione di ripartizione FΛ
del parametro Λ, con FΛ(0) = 0
Λ : variabile aleatoria che rappresenta la diversa propensione dei rischi
presenti nel portafoglio assicurativo
FΛ si prefigge di descrivere l’eterogeneità dei rischi del portafoglio
attribuibile ad alcune caratteristiche non adeguatamente valutabili
all’epoca di stipulazione del contratto
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione mistura di Poisson
9 OSSERVAZIONE:
OSSERVAZIONE rappresenta l’estensione,
estensione al caso
continuo,
continuo della mistura finita di Poisson.
Poisson
MEDIA E VARIANZA
E(N) = E[E(N|Λ)] = E(Λ)
var(N) = E(Λ) + var(Λ)
var(N) > E(N)
e la differenza è data da var(Λ), aspetto positivo per il modello
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione mistura di Poisson
¾ Scelta delle Funzione Peso:
MODELLO POISSON-GAMMA
Se il parametro Λ è rappresentato da una distribuzione gamma
di parametri positivi α e β, con densità (per λ > 0):
βα α −1 −β λ
f Λ (λ ) =
λ e
,
Γ (α )
Funzione gamma
+∞
Γ( u ) =
∫
x u −1 e − x dx
0
integrale finito per u > 0
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
MODELLO POISSON-GAMMA
βα + ∞ α + k −1 − (β +1)λ
pk =
e
dλ
λ
∫
Γ(α) k! 0
α
⎛ α + k − 1⎞ ⎛ β ⎞ ⎛ 1 ⎞
= ⎜⎜
⎟⎟ ⎜
⎟
⎟ ⎜
k
⎝
⎠ ⎝ β + 1⎠ ⎝ β + 1⎠
k
.
equivale ad assumere che il numero di sinistri, N,
abbia distribuzione binomiale negativa
β
di parametri r e q, con r = α e q =
β +1
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
MODELLO POISSON-GAMMA
9 OSSERVAZIONE
Differenza tra il Modello Poisson-gamma e la distribuzione
Binomiale Negativa:
nel modello Poisson-gamma il numero dei sinistri (aleatorio) è
rappresentato da un parametro aleatorio in grado di dare
maggiore flessibilità
(possibilità di scelta dei parametri della funzione peso)
MEDIA E VARIANZA
E(N ) =
α
,
β
var( N ) =
α ( β + 1)
.
2
β
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
• Distribuzione mistura di Poisson
¾ Scelta delle Funzione Peso:
MODELLO POISSON-GAUSSIANA INVERSA
Se il parametro Λ è rappresentato da una
distribuzione gaussiana inversa
di parametri positivi ν e ς, con densità (per λ > 0):
f Λ (λ ) =
ν
2πζλ3
e
(λ − ν ) 2
−
2ζλ
.
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
MODELLO POISSON-GAUSSIANA INVERSA
pk = p0
k k −1
ν
k!
∑
j= 0
(k − 1 + j)! ⎛ ζ ⎞
⎜ ⎟
(k − 1 − j)! j! ⎝ 2ν ⎠
per k=1,2,…
con p0 = e
ν (1− 1+ 2ζ )
ζ
.
j
k+ j
−
(1 + 2ζ ) 2
,
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
MODELLO POISSON-GAUSSIANA INVERSA
• PROPRIETÀ
La distribuzione Poisson-gaussiana inversa
soddisfa (per k = 2,3,…) la formula ricorrente
ς(2k − 3)
ν2
pk =
p k −1 +
pk −2 ,
(1 + 2ς)(k − 1)
(1 + 2ς)k ( k − 1)
con p1 = p 0
ν
1 + 2ς
La distribuzione del numero di sinistri
MODELLI PROBABILISTICI
MODELLO POISSON-GAUSSIANA INVERSA
MEDIA E VARIANZA
E(N) = ν
var(N) = ν (1+ς) .
var(N) > E(N)
La distribuzione del numero di sinistri
ASIMMETRIE DELLE DISTRIBUZIONI
• Coefficiente di asimmetria
E[( N − E ( N )) 3 ]
γ (N ) =
[var( N )] 3 / 2
Le distribuzioni del numero di
sinistri osservate in pratica,
seppur con differenze non
trascurabili tra i vari rami danni,
sono tipicamente caratterizzate
da asimmetria positiva.
I modelli presi in considerazione
per descrivere la distribuzione
del numero di sinistri presentano
un coefficiente di asimmetria
positivo per qualunque valore
possa essere assunto dai
parametri del modello
La distribuzione del numero di sinistri
ASIMMETRIE A CONFRONTO
• Coefficienti di asimmetria a confronto
¾
¾
1
γ ( N) =
λ
γ (N ) =
distribuzione di Poisson
2−q
distribuzione Binomiale negativa
r (1 − q)
ψ (σ 2 − μ ) 2 ⎤
1 ⎡ 2
¾ γ ( N) = 3 ⎢3σ − 2μ +
⎥,
μ
σ ⎣
⎦
distribuzione
Mistura di Poisson
- con μ = E(N), σ = [var(N)]½ ;
- mentre la costante reale ψ dipende dalla distribuzione del parametro Λ
La distribuzione del numero di sinistri
ASIMMETRIE A CONFRONTO
• Coefficienti di asimmetria a confronto
ψ (σ 2 − μ ) 2 ⎤
1 ⎡ 2
¾ γ ( N) = 3 ⎢3σ − 2μ +
⎥,
μ
σ ⎣
⎦
con μ = E(N), σ = [var(N)]½
e
distribuzione
Mistura di Poisson
ψ=2
ψ=3
MODELLO
POISSON-GAMMA
MODELLO
POISSON-GAUSSIANA INVERSA
La distribuzione del numero di sinistri
ASIMMETRIE A CONFRONTO
Il modello Poisson-gaussiana inversa presenta
(a parità di valore atteso e di varianza)
una maggiore asimmetria (positiva)
rispetto al modello Poisson-gamma.
Il modello Poisson-gaussiana inversa realizza
frequentemente un migliore adattamento ai dati osservati
La distribuzione di probabilità
del danno
Zi: variabile aleatoria che rappresenta il danno relativo all’i-esimo sinistro,
sinistro
le cui possibili determinazioni sono i numeri reali
Individuare i modelli probabilistici più adeguati per
descrivere la distribuzione di probabilità
del danno Z
IPOTESI:
Z è rappresentata da una distribuzione di probabilità continua e
dotata di densità fZ(x) continua per ogni x > 0
La distribuzione del danno
MODELLI PROBABILISTICI
Modelli più frequentemente adottati
(1) distribuzione Esponenziale;
(2) distribuzione di Weibull;
(3) distribuzione Gamma;
(4) distribuzione Lognormale;
(5) distribuzione di Pareto:
(6) distribuzione mistura di Esponenziali
a) modello Esponenziale-gamma
La distribuzione del danno
• DISTRIBUZIONE ESPONENZIALE
di parametro positivo v
f Z ( x) = v e
− vx
Reciproco del danno atteso
relativo a un sinistro che
colpisce il contratto nel
periodo di copertura
MEDIA E VARIANZA
1
E(Z ) =
v
1
var( Z ) = 2
v
La distribuzione del danno
DISTRIBUZIONE ESPONENZIALE
PROPRIETÀ della distribuzione Esponenziale
Proprietà di mancanza di memoria:
se Z ha distribuzione
esponenziale di
parametro v
anche (Z – c) | Z > c ha
distribuzione esponenziale
di parametro v
9 OSSERVAZIONE: La proprietà di mancanza di memoria
risulta utile in coperture assicurative caratterizzate dalla
presenza di una franchigia assoluta
La distribuzione del danno
• DISTRIBUZIONE DI WEIBULL
di parametri positivi v e δ
f Z ( x) = v δ x
δ −1
e
− vx δ
9 OSS: Posto δ = 1 si ha la distribuzione esponenziale di
parametro v
MEDIA E VARIANZA
1/ δ
⎛1⎞
E(Z ) = ⎜ ⎟
⎝v⎠
1/ δ
⎛1⎞
var( Z ) = ⎜ ⎟
⎝v⎠
1⎞
⎛
Γ⎜1 + ⎟
⎝ δ⎠
2
⎧⎪ ⎛
2⎞ ⎡ ⎛
1 ⎞⎤ ⎫⎪
⎨ Γ⎜ 1 + ⎟ − ⎢ Γ⎜ 1 + ⎟⎥ ⎬
⎪⎩ ⎝ δ ⎠ ⎣ ⎝ δ ⎠⎦ ⎪⎭
La distribuzione del danno
• DISTRIBUZIONE GAMMA
di parametri positivi α e v
vα
f Z ( x) =
xα −1 e −vx
Γ(α )
9 OSS: Posto α = 1 si ha la distribuzione esponenziale di
parametro v
MEDIA E VARIANZA
E(Z ) =
α
v
α
var( Z ) = 2
v
La distribuzione del danno
• DISTRIBUZIONE LOGNORMALE
di parametri μ e σ, con σ > 0
f Z ( x) =
1
2π σ x
e
(log x − μ ) 2
−
2σ 2
MEDIA E VARIANZA
E(Z ) = e
μ+
σ2
2
(
var( Z ) = e
2 μ +σ 2
)(e )
σ 2 −1
La distribuzione del danno
LA DISTRIBUZIONE LOGNORMALE
9 OSSERVAZIONE
In base al teorema centrale del limite,
la distribuzione lognormale è adatta a rappresentare il danno
nell’ipotesi (poco realistica) che esso sia generato da un
numero sufficientemente grande di caratteristiche del rischio:
- indipendenti,
- identicamente distribuite
- operanti in senso moltiplicativo
La distribuzione del danno
• DISTRIBUZIONE DI PARETO
di parametri positivi η e θ
f Z ( x) =
ηθ
η
(θ + x )η +1
MEDIA E VARIANZA
E(Z ) =
var( Z ) =
θ
η −1
ηθ
,
2
(η − 1) (η − 2)
2
se η > 1
,
se η > 2
La distribuzione del danno
LA DISTRIBUZIONE DI PARETO
PROPRIETÀ della distribuzione di Pareto
se Z ha
distribuzione di Pareto
di parametri η e θ
(Z – c) | Z > c ha
distribuzione di Pareto
di parametri η e θ + c
9 OSSERVAZIONE:
Ancora una volta (analogamente al caso della distribuzione Esponenziale),
è evidente l’utilità di tale proprietà in coperture assicurative
caratterizzate dalla presenza di una franchigia assoluta
La distribuzione del danno
• DISTRIBUZIONE MISTURA
DI ESPONENZIALI
di parametro aleatorio positivo V
+∞
f Z ( x) =
∫
f Z |V ( x | v ) dFV ( v )
0
f Z |V ( x | v ) = v e − vx
Funzione peso (della mistura)
funzione di ripartizione FV
del parametro V, con FV (0) = 0
La distribuzione del danno
MISTURA DI ESPONENZIALI (1/5)
V : variabile aleatoria che rappresenta il reciproco del danno atteso
relativo a un sinistro che colpisce il contratto
nel periodo di copertura
FV (funzione peso) si prefigge di descrivere l’eterogeneità
dei rischi del portafoglio relativa all’importo dei sinistri
ed attribuibile ad alcune caratteristiche del rischio
non adeguatamente valutabili all’epoca
di stipulazione del contratto
La distribuzione del danno
MISTURA DI ESPONENZIALI (2/5)
MEDIA E VARIANZA
⎛1⎞
E ( Z ) = E[ E ( Z | V )] = E ⎜ ⎟
⎝V ⎠
⎡ ⎛ 1 ⎞⎤
⎛ 1 ⎞
var( Z ) = 2 E ⎜ 2 ⎟ − E ⎢ E ⎜ ⎟⎥
⎝V ⎠
⎣ ⎝ V ⎠⎦
2
Forte dipendenza dalla scelta della distribuzione
che rappresenta la variabile aleatoria
relativa al parametro V
La distribuzione del danno
MISTURA DI ESPONENZIALI (3/5)
¾ Scelta delle Funzione Peso:
Se il parametro V è rappresentato da una distribuzione gamma
di parametri positivi α e β, con densità (per λ > 0):
βα α −1 −β λ
f Λ (λ ) =
λ e
,
Γ (α )
Funzione gamma
+∞
Γ( u ) =
∫
x u −1 e − x dx
0
integrale finito per u > 0
MODELLO
ESPONENZIALE-GAMMA
La distribuzione del danno
MISTURA DI ESPONENZIALI (4/5)
MODELLO ESPONENZIALE-GAMMA
βα
f Z (x) =
Γ (α )
=
+∞
∫
v α e − ( x + β) v dv
0
α
αβ
(β + x )
α +1
.
equivale ad assumere che il danno abbia
distribuzione di Pareto di parametri η e θ,
con η = α e θ = β
La distribuzione del danno
MISTURA DI ESPONENZIALI (5/5)
MODELLO ESPONENZIALE-GAMMA
MEDIA E VARIANZA
E(Z ) =
β
α −1
,
se α > 1
αβ 2
var( Z ) =
,
2
(α − 1) (α − 2)
se α > 2
La distribuzione del danno
ASIMMETRIE DELLE DISTRIBUZIONI
• Coefficiente di asimmetria
E[( Z − E ( Z )) 3 ]
γ (Z ) =
[var(Z )] 3 / 2
Le distribuzioni del
danno osservato ,
seppur con differenze non
trascurabili tra i vari rami danni,
sono tipicamente caratterizzate
da asimmetria positiva.
I modelli presi in considerazione
per la distribuzione del danno,
(ad eccezione della distribuzione di Weibull:
coefficiente di asimmetria positivo solo
per valori di v inferiori a v* ≈ 3,6 )
presentano un coefficiente di
asimmetria positivo
per qualunque valore possa essere
assunto dai parametri
La distribuzione del danno
ASIMMETRIE A CONFRONTO
• Coefficienti di asimmetria a confronto
¾ γ(Z) = 2
2
¾ γ ( Z) =
α
distribuzione Esponenziale
distribuzione Gamma
σ2 +2 ⎞
σ2
⎛
⎟ e −1
¾ γ ( Z) = ⎜ e
⎝
⎠
¾
2 η − 2 (η + 1)
γ ( Z) =
η (η − 3)
distribuzione Lognormale
se η>3, distribuzione di Pareto
2 α − 2 (α + 1)
γ ( Z) =
se α >3,
α (α − 3)
modello Esponenziale-gamma
La distribuzione del danno
CODA (DESTRA) DELLA DISTRIBUZIONE (1/3)
• Probabilità relativa all’evento {Z > x}, per ogni x > 0
FZ ( x ) = 1 − FZ ( x )
DISTRIBUZIONI
a CODA LEGGERA
(“light tail”)
(ad esempio quelle riguardanti
varie coperture
per il rischio infortunio o malattia)
a CODA PESANTE
(“heavy tail”)
(ad esempio quelle riguardanti
le coperture del ramo
responsabilità civile aeromobili)
La distribuzione del danno
CODA (DESTRA) DELLA DISTRIBUZIONE (2/3)
• Code delle distribuzioni:
− vx
F
(
x
)
=
e
¾ Z
¾ FZ ( x ) = e
¾
distribuzione Esponenziale
− vx δ
⎛ θ ⎞
FZ ( x ) = ⎜
⎟
⎝θ+ x⎠
distribuzione di Weibull
η
distribuzione di Pareto
9 OSSERVAZIONE:
In genere la distribuzione esponenziale è adottata come “benchmark”
ai fini della classificazione delle distribuzioni del danno
in distribuzioni con coda leggera e distribuzioni con coda pesante.
La distribuzione del danno
CODA (DESTRA) DELLA DISTRIBUZIONE (3/3)
• Confronto tra distribuzioni
la distribuzione esponenziale ha
e − vx
una coda meno pesante
lim
=
0
η
x → +∞
rispetto alla distribuzione
⎛ θ ⎞
⎟
⎜
di Pareto
⎝θ + x ⎠
(la coda dell’esponenziale tende
più rapidamente a 0)
¾ La coda della distribuzione di Weibull risulta:
- compresa tra le altre due per 0 < δ < 1
- addirittura più leggera della coda della distribuzione esponenziale per δ > 1
¾ La distribuzione Gamma presenta una coda leggera
¾ La distribuzione Lognormale presenta una coda pesante
La distribuzione del danno
ANALISI DEI GRANDI SINISTRI (1/3)
• Grandi Sinistri (“Large Claims”):
sinistri caratterizzati da un danno ben più elevato
rispetto ai restanti sinistri osservati.
Carenza di dati statistici
Effetti negativi
(per l’assicuratore)
Utilizzare una base statistica riferita
ad un più ampio orizzonte temporale
• Reale praticabilità
• Soddisfazione nei risultati
derivanti da un’eventuale
sottovalutazione
La distribuzione del danno
ANALISI DEI GRANDI SINISTRI (2/3)
Risulta opportuno adottare MISURE PRUDENZIALI
¾ In particolare adottare un modello probabilistico
caratterizzato da una coda sufficientemente pesante
9 La distribuzione di Pareto è particolarmente adatta a tale scopo:
essa consente anche di ottenere un’espressione
analiticamente semplice per la probabilità FZ
La distribuzione del danno
ANALISI DEI GRANDI SINISTRI (3/3)
¾ È possibile generalizzare la distribuzione di Pareto
DISTRIBUZIONE DI BURR
Z=H
distribuzione di Burr
di parametri η, θ e d
con densità
η d θ η x d −1
f Z ( x) =
(θ + x d )η +1
1/ d
d>0
distribuzione di Pareto
di parametri η e θ
La distribuzione del danno
DISTRIBUZIONE DI BURR (1/2)
MEDIA E VARIANZA
θ
E(Z ) =
var( Z ) =
1/ d
1⎞ ⎛
1⎞
⎛
Γ⎜η − ⎟ Γ⎜1 + ⎟
d⎠ ⎝ d⎠
⎝
,
Γ(η )
2
2
θ 2 / d Γ⎛⎜η − ⎞⎟ Γ⎛⎜1 + ⎞⎟
⎝
d⎠ ⎝
Γ(η )
d⎠
se dη > 1
−
2
1⎞ ⎛
1 ⎞⎤
⎡ 1/ d ⎛
⎢θ Γ⎜η − d ⎟ Γ⎜1 + d ⎟ ⎥
⎠⎥ ,
⎠ ⎝
⎝
⎢
Γ(η )
⎢
⎥
⎢⎣
⎥⎦
se dη > 2
La distribuzione del danno
DISTRIBUZIONE DI BURR (2/2)
CODA DELLA DISTRIBUZIONE
θ
η
⎛
⎞
FZ ( x ) = ⎜
d ⎟
⎝θ + x ⎠
¾ Rispetto alla coda della distribuzione di Pareto,
la coda della distribuzione di Burr risulta:
- più pesante per 0 < d < 1 CASO DI INTERESSE
(utilmente impiegabile ai fini della descrizione del danno,
ad esempio, nelle assicurazioni di responsabilità civile aeromobili)
- più leggera per d > 1
Distribuzioni normalizzate (1/2)
• Nelle applicazioni assicurative le determinazioni relative alle
distribuzioni di probabilità sia del numero di sinistri che del danno
sono di norma contenute in un intervallo limitato I
¾ N: NUMERO DI SINISTRI
Intervallo di riferimento
I={0,1,…,nmax}
massimo numero
di sinistri probabile:
massimo numero di sinistri al quale
viene soggettivamente attribuita una
probabilità positiva di accadimento
¾ Z: DANNO
Intervallo di riferimento
I=(0,zmax)
- valore del bene nel caso di
un’assicurazione a beni di proprietà;
- massimo danno probabile
nel caso di un’assicurazione di
responsabilità civile.
Distribuzioni normalizzate (2/2)
Per descrivere la base tecnica del rischio vanno considerate
le distribuzioni (sia del danno che del numero dei sinistri) condizionate
all'ipotesi di appartenenza ai relativi intervalli di riferimento.
¾ N: NUMERO DI SINISTRI
a partire dalla probabilità, pk
pk
Pr{N = k | N ∈ I } =
,
pi
∑
i∈I
¾ Z: DANNO
k∈I
a partire dalla densità, fZ
f Z |Z∈I ( x ) =
∫
I
f Z ( x)
,
f Z ( x ) dx
x∈I
La distribuzione di probabilità
del risarcimento (1/5)
Yi: variabile aleatoria che rappresenta il risarcimento
relativo all’i-esimo sinistro.
sinistro
¾ La distribuzione di probabilità del risarcimento è
ottenibile a partire dalla distribuzione di probabilità del danno
tenuto anche conto delle condizioni contrattuali di copertura
riassunte dalla funzione di risarcimento, φ
(che individua la relazione tra danno e risarcimento)
Ad esempio la distribuzione del risarcimento può essere ottenuta
mediante TRONCAMENTO
(metodologia tipica in presenza di una limitazione
superiore al risarcimento del danno)
La distribuzione di probabilità
del risarcimento (2/5)
ESEMPIO di DISTRIBUZIONE TRONCATA
¾ Copertura di responsabilità civile con massimale di garanzia
(di importo M)
Risarcimento:
Y = min (Z, M)
Funzione di ripartizione del risarcimento:
⎧ FZ ( x )
FY ( x ) = ⎨
⎩ 1
se x < M
se x ≥ M
viene concentrata in M tutta
la restante massa di probabilità
9 Tale funzione di ripartizione è valida anche nel caso di
una copertura a primo rischio assoluto
La distribuzione di probabilità
del risarcimento (3/5)
¾ Copertura con franchigia assoluta (di importo f)
Risarcimento:
Y = max (0, Z - f)
Funzione di ripartizione
del risarcimento:
FY ( x ) = FZ ( x + f )
¾ Copertura con franchigia relativa (di importo f)
Risarcimento:
⎧0
Y=⎨
⎩Z
se Z ≤ f
se Z > f
Funzione di ripartizione
del risarcimento:
⎧ FZ (f )
FY ( x ) = ⎨
⎩ FZ ( x )
se x < f
se x ≥ f
La distribuzione di probabilità
del risarcimento (4/5)
¾ Copertura di responsabilità civile con massimale di
garanzia e franchigia assoluta
(rispettivamente, di importo M e f)
Risarcimento:
Y = min [ max (0, Z - f), M - f]
Funzione di ripartizione del risarcimento:
⎧ FZ ( x + f )
FY ( x ) = ⎨
1
⎩
se x < M − f
se x ≥ M − f
La distribuzione di probabilità
del risarcimento (5/5)
¾ Copertura con scoperto (di aliquota ξ)
Risarcimento:
Y = (1 - ξ) Z
Funzione di ripartizione del risarcimento:
⎛ x ⎞
FY ( x ) = FZ ⎜⎜
⎟⎟
⎝1− ξ ⎠
9 OSSERVAZIONE: In conclusione, si osserva come ai fini dei calcoli
(relativi ad ogni tipo di copertura assicurativa) è sufficiente esprimere la
variabile aleatoria risarcimento in funzione della variabile aleatoria danno
seguendo la relazione esistente tra le due entità.
La distribuzione di probabilità
del risarcimento globale (1/2)
X: variabile aleatoria che rappresenta il risarcimento globale.
Ricavare i modelli probabilistici più frequentemente
adottati per descrivere la distribuzione di probabilità
del risarcimento globale X sulla base delle scelte
effettuate con riferimento alle variabili aleatorie
numero di sinistri e danno (risarcimento)
IPOTESI:
La funzione di ripartizione di X è definita, per ogni x ≥ 0, da:
+∞
FX ( x ) = ∑ pk FYk * ( x ) , con FX(0) = p0 se è Y = Z
k =0
La distribuzione di probabilità
del risarcimento globale (2/2)
Se il risarcimento Y ha distribuzione esponenziale
di parametro v
• Convoluzione k-esima:
k −1
F ( x) = 1 − ∑
k*
Y
i =0
(vx )i e − vx
i!
• Funzione di ripartizione del risarcimento globale:
⎡ k −1 ( vx)i e − vx ⎤
FX ( x ) = p 0 + ∑ p k ⎢1 − ∑
⎥
i
!
k =1
⎦
⎣ i =0
+∞
= 1−
+∞
k −1
k =1
i =0
∑ pk ∑
( vx )i e − vx
.
i!
La distribuzione del risarcimento globale
MODELLI PROBABILISTICI
Modelli più frequentemente adottati
(1) distribuzione di Poisson composta;
(2) distribuzione Binomiale negativa composta;
(3) distribuzione mistura di Poisson composta;
La distribuzione del risarcimento globale
• DISTRIBUZIONE DI POISSON COMPOSTA
¾ Il numero di sinistri N ha distribuzione di Poisson
di parametro λ
Distribuzione
di N (Poisson)
+∞
FX ( x ) = ∑ e −λ
k =0
λk
k!
FYk * ( x )
Distribuzione di Poisson composta di parametri λ e FY
La distribuzione del risarcimento globale
DISTRIBUZIONE DI POISSON COMPOSTA (1/3)
• ESEMPIO
Nel caso in cui risarcimento Y ha distribuzione esponenziale
di parametro v
FX ( x ) = 1 − e
−( λ + vx )
+∞
∑
k =1
λk
k!
k −1
∑
i =0
( vx )i
i!
La distribuzione del risarcimento globale
DISTRIBUZIONE DI POISSON COMPOSTA (2/3)
• PROPRIETÀ
Se X1, X2, …, XS sono S v.a. indipendenti e
X h = ∑iN=h0 Yi, h
(h=1,2,…,S)
ha distribuzione di Poisson composta di parametri λh e FY
h
X
TOT
=
S
∑ Xh
h =1
ha distribuzione di Poisson composta
di parametri λ e FY , con
S
λ = ∑ λh
h =1
S
FY ( x ) = ∑
h =1
⎛ λh ⎞
⎜ ⎟ FYh ( x )
⎝λ⎠
La distribuzione del risarcimento globale
DISTRIBUZIONE DI POISSON COMPOSTA (3/3)
9 OSSERVAZIONE:
Se X1, X2, …, XS sono anche identicamente distribuite
con distribuzione di Poisson composta
di parametri λ e FY,
allora
i parametri di XTOT sono rispettivamente
λ = Sλ
e
F Y = FY
La distribuzione del risarcimento globale
• DISTRIBUZIONE BINOMIALE
NEGATIVA COMPOSTA
¾ Il numero di sinistri N ha distribuzione Binomiale
negativa di parametri r e q
Distribuzione di N
(Binomiale negativa)
+∞
FX ( x ) = ∑
k =0
( r )k r
q (1 − q)k FYk * ( x )
k!
Distribuzione Binomiale negativa composta
di parametri r, q e FY
La distribuzione del risarcimento globale
DISTRIBUZIONE BINOMIALE NEGATIVA COMPOSTA
• PROPRIETÀ
Se X1, X2, …, XS sono S v.a.
- indipendenti
- identicamente distribuite con distribuzione binomiale
negativa composta di parametri r, q e FY
X TOT =
S
∑ Xh
h =1
ha distribuzione
Binomiale negativa composta
di parametri Sr, q e FY
La distribuzione del risarcimento globale
• DISTRIBUZIONE MISTURA DI
POISSON COMPOSTA
¾ Il numero di sinistri N ha distribuzione mistura di Poisson
di parametro aleatorio Λ
Distribuzione di N
(Mistura di Poisson)
⎞ k*
⎛ +∞ −λ λk
FX ( x ) = ∑ ⎜⎜ ∫ e
dFΛ (λ ) ⎟⎟ FY ( x )
k!
k =0 ⎝ 0
⎠
+∞
Distribuzione mistura di Poisson composta
di parametri Λ e FY
Calcolo dei principali momenti del
risarcimento globale (1/13)
¾ Le principali valutazioni attuariali (calcolo del premio,
valutazione delle riserve tecniche, …) di norma richiedono la
conoscenza di almeno i primi due momenti
del risarcimento globale X
• Nelle ipotesi classiche della teoria del rischio
(indipendenza tra numero di sinistri e danni, risarcimenti indipendenti
ed identicamente distribuiti)
VALORE ATTESO
E ( X ) = E [ E ( X | N )] = E ( N ) E (Y )
Fattorizzazione del valore atteso
nel numero di sinistri e nel
risarcimento
Calcolo dei principali momenti del
risarcimento globale (2/13)
MOMENTO SECONDO
E ( X 2 ) = E ( N ) var(Y ) + E ( N 2 ) [ E (Y )]2
VARIANZA
var( X ) = E ( N ) var(Y ) + var( N ) [ E (Y )]
2
Calcolo dei principali momenti del
risarcimento globale (3/13)
MOMENTI DI ORDINE SUPERIORE AL SECONDO
• Funzione generatrice dei momenti
M X (τ ) = E ( eτX ) =
+∞
∫
eτx dFX ( x ) ,
−∞
posto che il valore atteso esista finito in un intorno dell'origine
(vale a dire, per |τ| ≤ τ0)
• Il momento r-esimo (r = 1,2,…) di X
dr
μr ( X ) =
M X (τ )
r
dτ
τ =0
Ricordiamo che
μr(X) = E(Xr)
Calcolo dei principali momenti del
risarcimento globale (4/13)
FUNZIONE GENERATRICE DEI MOMENTI
• Nelle date ipotesi probabilistiche
M X (τ ) = E [ E ( eτX | N )] = E [( M Y (τ )) N ]
= M N [log M Y (τ )]
funzione generatrice
dei momenti
del numero di sinistri
funzione generatrice
dei momenti
del risarcimento
¾ La funzione generatrice dei momenti del risarcimento globale
si ricava a partire dalle funzione generatrice dei momenti
- del numero di sinistri
- del risarcimento
Calcolo dei principali momenti del
risarcimento globale (5/13)
FUNZIONE GENERATRICE DEI MOMENTI
• PROPRIETÀ
Se X1, X2, …, XS sono S v.a.
- indipendenti
- con funzioni generatrici dei momenti:
+∞
( ) ∫e
M X h (τ ) = E eτX h =
−∞
M X TOT (τ ) =
τx
dFX h ( x ) per MX1, MX2, …, MXS
S
∏
h =1
M X h (τ ) dove X
TOT
=
S
∑ Xh
h =1
Calcolo dei principali momenti del
risarcimento globale (6/13)
FUNZIONE GENERATRICE DEI SEMINVARIANTI
(o, anche, funzione generatrice dei cumulanti)
ΨX (τ ) = log M X (τ )
= ΨN [ ΨY (τ )]
funzione generatrice
dei seminvarianti
del numero di sinistri
funzione generatrice
dei seminvarianti
del risarcimento
¾ La funzione generatrice dei seminvarianti:
-si ricava a partire dalla funzione generatrice dei momenti
- si esprime mediante la funzione generatrice dei seminvarianti
del numero dei sinistri e del risarcimento.
Calcolo dei principali momenti del
risarcimento globale (7/13)
FUNZIONE GENERATRICE DEI SEMINVARIANTI
• Seminvariante (o cumulante) r-esimo (r = 1,2,…) di X
dr
κr ( X ) =
ΨX (τ )
r
dτ
τ =0
¾ κ 1 ( X ) = μ1 ( X ) = E ( X )
2
¾ κ 2 ( X ) = μ2 ( X ) − [ μ1 ( X )] = var( X )
3
'
¾ κ 3 ( X ) = μ3 ( X ) − 3μ1 ( X ) μ2 ( X ) + 2[ μ1 ( X )] = μ3 ( X )
μ3' ( X ) momento centrale terzo di X, E [( X − E ( X )) 3 ]
Calcolo dei principali momenti del
risarcimento globale (8/13)
FUNZIONE GENERATRICE DEI SEMINVARIANTI
• PROPRIETÀ
Se X1, X2, …, XS sono S v.a.
- indipendenti
- con funzioni generatrici dei seminvarianti:
ΨX h (τ) = log M X h (τ) , per ΨX , ΨX , …, ΨX
1
ΨX TOT (τ ) =
S
∑Ψ
h =1
Xh
(τ )
dove X
2
TOT
S
=
S
∑ Xh
h =1
Calcolo dei principali momenti del
risarcimento globale (9/13)
SEMINVARIANTI
¾ Dalla proprietà della funzione generatrice dei seminvarianti
κr ( X
TOT
S
) = ∑ κ r (X h )
h =1
i seminvarianti di v.a. indipendenti godono della proprietà additiva
¾ Seminvarianti e Coefficiente di asimmetria
E [( X − E ( X )) 3 ]
κ3( X )
γ (X ) =
=
3/ 2
[var( X )]
[κ 2 ( X )]3 / 2
Calcolo dei principali momenti del
risarcimento globale (10/13)
Valore atteso, varianza e funzione generatrice dei momenti
nel caso in cui il risarcimento globale, X, abbia:
(1) distribuzione di Poisson composta;
(2) distribuzione Binomiale negativa composta;
(3) distribuzione mistura di Poisson composta;
Calcolo dei principali momenti del
risarcimento globale (11/13)
• DISTRIBUZIONE DI POISSON COMPOSTA
di parametri λ e FY
VALORE ATTESO
VARIANZA
E ( X ) = λ E (Y )
var( X ) = λ E (Y 2 )
FUNZIONE GENERARICE DEI MOMENTI
M X (τ ) = eλ [ log M Y (τ )−1]
Calcolo dei principali momenti del
risarcimento globale (12/13)
• DISTRIBUZIONE BINOMIALE
NEGATIVA COMPOSTA
di parametri r, q e FY
VALORE ATTESO
r (1 − q)
E( X ) =
E (Y )
q
r (1 − q)
r (1 − q)
2
VARIANZA var( X ) =
var(Y ) +
[
E
(
Y
)]
q
q2
FUNZIONE GENERARICE DEI MOMENTI
qr
M X (τ ) =
[1 − (1 − q ) log M Y (τ )]r
Calcolo dei principali momenti del
risarcimento globale (13/13)
• DISTRIBUZIONE MISTURA DI
POISSON COMPOSTA
di parametri Λ e FY
VALORE ATTESO
VARIANZA
E ( X ) = E ( Λ ) E (Y )
var( X ) = E ( Λ ) E (Y ) + var(Λ ) [ E (Y )]
2
FUNZIONE GENERARICE DEI MOMENTI
M X (τ ) = M Λ [ log M Y (τ ) − 1 ]
2
Calcolo dei principali momenti del risarcimento globale
OSSERVAZIONI
1) ASIMMETRIA DELLE DISTRIBUZIONI:
- la distribuzione di Poisson composta e la distribuzione Binomiale
negativa composta hanno un coefficiente di asimmetria positivo per
qualunque valore possa essere assunto dai parametri del modello;
- tale risultato, in generale, non è invece valido nel caso della distribuzione
mistura di Poisson composta.
2) DISTRIBUZIONE DI POISSON COMPOSTA E MISTURA DI
POISSON COMPOSTA A CONFRONTO:
- a parità di valore atteso, E(λ)= λ, la distribuzione mistura di Poisson
composta ha varianza superiore;
superiore
2
- il termine aggiuntivo,
aggiuntivo var( Λ ) [ E (Y )] , dipende dalla varianza del
parametro aleatorio Λ.
Maggiore flessibilità del modello
mistura di Poisson Composta rispetto
al modello di Poisson composta
LE ASSICURAZIONI
SULLA DURATA VITA
La base tecnica del rischio
La base tecnica del rischio
•
Le basi tecniche rappresentano le ipotesi fissate al momento della stipula del
contratto e che non possono essere variate nel corso del contratto.
l’ipotesi demografica: tale ipotesi esprime la probabilità di verificarsi
dell’evento. Può essere calcolata o definendo apposite leggi analitiche in
grado di rappresentare la durata di vita oppure costruendo delle tavole di
sopravvivenza (strada adottata nella pratica).
l’ipotesi finanziaria: tale ipotesi si basa sulla determinazione di un
tasso (pari alle aspettative di rendimento future) sulla base del quale
viene calcolato il premio. In realtà con l’introduzione di polizze
rivalutabili prima e delle nuove tipologie (index e unit linked) tale
ipotesi viene riformulata in modo differente.
Aspetti demografici
¾ La funzione di sopravvivenza……..
•
•
•
Una testa alla nascita (x = 0)
T0 durata aleatoria di vita della testa x
La funzione di ripartizione della variabile aleatoria:
F0 (t ) = Ρ{T0 ≤ t}
•
La funzione di sopravvivenza è quindi:
S (t ) = Ρ{T0 > t} = 1 − F0 (t )
Aspetti demografici
¾ …..in generale per una testa di età x
• Per l’età
x = 0,1,2,..., ω − 1
Tx = (T0 − x )T0 > x
• La funzione di ripartizione per la generica età x:
Fx (t ) = Ρ{Tx ≤ t} = Ρ{T0 ≤ x + t T0 > x} =
Ρ{x ≤ T0 ≤ x + t} F0 ( x + t ) − F0 ( x )
=
=
=
Ρ{T0 > x}
1 − F0 ( x )
S (x ) − S (x + t )
S (x + t )
=
= 1−
S (x )
S (x )
Aspetti demografici
¾ Probabilità di vita e di morte
S (x + t )
⇒
t qx = 1 −
S (x )
S x+t
⇒
t px =
Sx
• Probabilità che la testa di età
attuale x deceda entro t anni.
• Probabilità che la testa di età
attuale x sopravviva t anni.
Aspetti demografici
¾ Tavola di sopravvivenza
• Nella pratica attuariale si usa costruire un modello probabilistico discreto,
partendo dall’osservazione di una tavola l x (numero probabile di viventi
all’età x) ricavata da osservazioni statistiche;
• Si suppone che la collettività sia chiusa a nuovi ingressi e che l’unica causa
d’uscita sia il decesso.
• Si stabilisce un’età estrema ω, intesa come un’età che concretamente non è
raggiungibile da un individuo.
• Si definisce tavola di sopravvivenza, il numero dei viventi per ogni età intera
a, a+1, a+2,…, ω-1,
l a , l a +1 ,..., lω −1
Aspetti demografici
¾ Elementi della tavola
• Probabilità di decesso tra l’età x e
l’età x+1
• Probabilità di sopravvivenza tra
l’età x e l’età x+1
• Soggetti deceduti in età x
• Soggetti sopravvissuti all’età x
qx
px = 1 − qx
d x = lx ⋅ qx
l x +1 = l x ⋅ p x
Aspetti demografici
¾ Costruzione della tavola
• Ad una popolazione fittizia di 100.000 unità vengono applicate le
probabilità di sopravvivenza ricavate dai dati di censimento:
q 0 = 0,00879 ⇒ (1 − q 0 ) = p 0 = 0,99121
l 0 = 100000
l1 = l 0 ⋅ p 0 = 100000 ⋅ 0,99121 = 99121
Aspetti demografici
¾ La tavola di mortalità
età
qx
px = 1 − qx
lx
dx
0
0,00879
0,99121
100000
879
1
0,000454
0,999546009
99121
45
2
0,000333
0,999666922
99076
33
3
0,000252
0,999747584
99043
25
4
0,000212
0,999787917
99018
21
5
0,000202
0,999797974
98997
20
6
0,000202
0,999797933
98977
20
7
0,000202
0,999797892
98957
20
8
0,000192
0,999807959
98937
19
Aspetti demografici
¾ La tavola di mortalità
• La tavola di sopravvivenza indica per una collettività chiusa a nuovi ingressi il
numero di viventi alle diverse età x.
• Tali tavole, poi utilizzate nel mercato assicurativo vengono costruite con
rilevazioni per contemporanei nel corso delle indagini censuarie.
Eta'
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Sopravviventi Decessi Probabilità di morte (per mille) Speranza di vita
100000
521
5,20828
76,541
99479
28
0,28554
75,939
99451
22
0,2247
74,961
99428
18
0,17836
73,978
99411
15
0,14676
72,991
99396
14
0,13678
72,001
99383
13
0,12822
71,011
99370
13
0,12666
70,02
99357
12
0,12132
69,029
99345
12
0,11581
68,037
99334
12
0,12307
67,045
99321
14
0,13802
66,053
99308
17
0,17028
65,062
99291
23
0,2267
64,073
99268
29
0,29334
63,088
99239
37
0,37697
62,106
99202
49
0,49352
61,129
99153
60
0,60776
60,159
99093
73
0,73771
59,196
99019
85
0,85959
58,239
98934
92
0,92733
57,289
Breve estratto dalle Tavole Istat 2000 per la popolazione maschile
Dal momento che i contratti di
assicurazione sulla vita, possono
avere una durata particolarmente
rilevante occorre:
una scelta opportuna delle tavole
di sopravvivenza
una costante revisione nei nuovi
contratti da parte delle imprese
delle basi demografiche alla luce
degli scenari evolutivi
Aspetti demografici
¾ L’invecchiamento della popolazione italiana
anno
Struttura per età della popolazione italiana 1990-2050
%0-14
%15-64
%65+
%85+
1990
16,8
68,5
14,7
1,2
2005
14,2
66,4
19,5
2,0
2010
14,0
65,5
20,5
2,8
2020
13,2
63.7
23,2
3,9
2030
12,2
60,8
27,0
4,7
2040
12,4
55,6
32,0
5,8
2050
12,7
53,7
33,6
7,8
Aspetti demografici
¾ L’effetto longevity
LONGEVITY RISK:
Possibilità che l’evoluzione della mortalità sia diversa rispetto a quella prevista:
in particolare possibilità che la mortalità sia inferiore a quella attesa.
2005
2030
2050
Uomini
77,4
81,0
83,6
Donne
83,3
86,6
88,8
Vita media
Aspetti demografici
¾ L’effetto longevity
Le analisi dell’andamento della curva di sopravvivenza (probabilità di
sopravvivenza alle diverse età) nel corso degli anni hanno mostrato un:
- processo di espansione
- processo di rettangolarizzazione
Curve di sopravvivivenza popolazione
maschile italiana
sim51
sim61
sim71
sim81
sim91
istat98
istat99
1
0,75
0,5
0,25
0
0
20
40
60
80
100
Aspetti demografici
¾ L’effetto longevity: CONSEGUENZE
• Importanza della valutazione accurata dei costi e della scelta delle basi
tecniche nei prodotti che erogano prestazioni previdenziali e
assicurative
• Possibilità di incorrere in un rischio sistematico (longevity risk)
• Tentativo di trasferimento del rischio verso gli assicurati:
- coefficienti di conversione non garantiti
- erogazione di rendite esclusivamente finanziarie (rendite certe)
• Facoltà di ricorso alla riassicurazione
• Costruzione di tavole proiettate
Aspetti demografici
¾ L’effetto longevity
Le principali forme assicurative soggette al rischio Longevity sono le seguenti:
- Rendite vitalizie immediate
- Rendite in corso di godimento derivanti da opzioni
- Rendite differite
- Tariffe con opzione di rendita
- Fondi pensionistici individuali (FIP)
Aspetti demografici
¾ L’effetto longevity: POSSIBILI RIMEDI (1/2)
Per la gestione del Longevity Risk, si agisce:
- a priori, adottando opportune politiche di:
tariffazione: utilizzo di tavole demografiche proiettate e selezionate, porre limitazioni
rispetto all’epoca in cui verranno riconosciute le garanzie o rispetto alla portata della
garanzia offerta
riassicurazione: Non è di uso comune per la difficoltà di trovare riassicuratori
disposti a coprire questo rischio, anche per le difficoltà di valutazione. Sempre più spesso
i riassicuratori preferiscono offrire il loro supporto in fase di pricing delle garanzie (studio
delle dinamiche della mortalità, revisione delle basi demografiche, ecc.)
- a posteriori
in sede di calcolo della riserva: L’utilizzo di tavole proiettate non elimina completamente
il longevity risk e comunque le compagnie hanno in portafoglio molti contratti di rendita stipulati
precedentemente all’entrata in vigore delle tavole proiettate .
E’ pertanto necessario, in sede di bilancio, provvedere ad una integrazione di riserva per
tener conto della sopravvivenza reale degli assicurati rispetto a quella prevista dalle
basi di primo
ordine.
Un obbligo in tal senso è attualmente previsto dall’articolo 26 del decreto legislativo 174 del
17/3/95, successivamente precisato dal provvedimento ISVAP n° 1380 del 22/12/1999.
Aspetti demografici
¾ L’effetto longevity: POSSIBILI RIMEDI (2/2)
Un netto miglioramento nella tariffazione deriva dall’utilizzo di tavole demografiche
costruite in base ai concetti di proiezione e di selezione.
Proiezione:
Una tavola proiettata è una tavola costruita in modo tale da tener conto della prevista
evoluzione della mortalità entro un certo periodo. Un metodo per realizzare questo è costruire
una tavola demografica “per generazioni”, con quozienti di mortalità variabili non soltanto in
base all’età, ma anche alla generazione di appartenenza.
Selezione:
Una tavola selezionata è una tavola applicabile a particolari gruppi di assicurati ottenuta
variando la mortalità di tavole “standard” in funzione dell’effettiva mortalità rilevata in
precedenza per tali gruppi.
A partire dal 1999 il mercato italiano,recependo le disposizioni della circolare ISVAP n°
343 del 1998, utilizza, per le assicurazioni di rendita, la tavola RG48.
Il monitoraggio eseguito dall’ANIA su un campione rappresentativo di alcune compagnie
italiane ha evidenziato alcuni problemi di “tenuta” della base demografica RG48 nelle età
anziane.
Aspetti demografici
¾ L’effetto longevity: LE TAVOLE A CONFRONTO
Tavole Istat 2000: Tavole di sopravvivenza pubblicate dall’Istat
Tavole RG48sel: tavole selezionate e proiettate costruite dalla Ragioneria Generale dello Stato
Tavole IPPsel: tavole proiettate e selezionate, recentemente presentate dall’Ania
Confronto Tavole Maschili
Confronto Tavole Femminili
100000
100000
80000
80000
60000
60000
40000
40000
20000
20000
Istat00M
IPPselF
rg48selF
Istat00F
40
50
80
90
10
0
11
0
rg48selM
60
70
IPPselM
20
30
0 10 20 30 40 50 60 70 80 90 100 110
0
10
0
0
Aspetti finanziari
• L’altro aspetto fondamentale nel vita riguarda la scelta del tasso tecnico
a cui valutare i contratti di assicurazione.
• Il tasso tecnico risulta di fondamentale importanza sia per il calcolo del
premio sia per il calcolo delle riserve.
• A differenza dei contratti di assicurazione contro i danni, i contratti di
assicurazione sulla vita presentano una durata di medio lungo periodo e
non è quindi possibile trascurare l’aspetto finanziario.
• È dunque opportuno effettuare una adeguata scelta del tasso tecnico
anche in relazione ai possibili investimenti delle riserve con i
conseguenti rendimenti prevedibili
Aspetti finanziari
IL TASSO TECNICO
• Il tasso tecnico viene fissato al momento della sottoscrizione del
contratto.
• La scelta del tasso tecnico risulta particolarmente delicata in quanto
l'assicuratore garantisce tale rendimento all'assicurato già nel calcolo
del premio e della prestazione (dunque alla stipula del contratto e per
tutta la durata contrattuale).
• Il tasso tecnico deve comunque essere inferiore ad un tasso massimo
garantibile fissato, a tutela degli assicurati, dalla normativa e variabile
in funzione dei rendimenti dei titoli obbligazionari (tale tasso massimo
è determinato con regolamento dell'ISVAP ma non può superare il
60% del tasso medio dei prestiti obbligazionari – art. 33 Codice delle
Assicurazioni).
La base tecnica del rischio
• Il tasso tecnico e la tavola di mortalità (i, q) rappresentano
la base tecnica del rischio
• Occorre distinguere in:
BASE TECNICA DEL
PRIMO ORDINE
BASE TECNICA DEL
SECONDO ORDINE
Il calcolo del premio viene effettuato sulla base delle basi tecniche
scelte, delle caratteristiche dell’assicurato (età e sesso) e delle
caratteristiche contrattuali (tipologia di premio e prestazione, durata)
IL PREMIO
considerazioni generali
La scomposizione del premio
•
Il premio assicurativo:
- premio equo: basato sul principio di “equità finanziaria e attuariale”.
• Il valore atteso della perdita L deve essere nullo alla stipula del contratto:
~
E ( L ) = 0 → E ( I x( c ) ) = E ( I x( a ) ) → PU = E ( I x( a ) )
• In altre parole: il valore attuale atteso delle prestazioni dell’assicuratore
deve coincidere con il valore attuale atteso delle prestazioni dell’assicurato
- premio netto: pari ad un premio equo più un caricamento di sicurezza
(implicito o esplicito). Il caricamento ha lo scopo sia di far fronte ad
eventuali scostamenti in negativo delle realtà rispetto alle ipotesi fatte
(basi tecniche), sia di garantire un margine di profitto alla compagnia.
- premio di tariffa: pari al premio netto più i caricamenti per spese.
I caricamenti
Esistono generalmente tre tipi di caricamenti per spese:
per spese di acquisizione (provvigioni d’acquisto,spese di emissione
polizza, spese per visite mediche ed accertamenti). Si tratta di spese
sostenute generalmente al momento della stipula del contratto o comunque
nel primo anno di durata contrattuale
per spese di incasso (provvigioni di incasso, diritti di quietanza,
contabilizzazione dell’introito). Si tratta di spese che vengono sostenute in
corrispondenza dell’incasso della rata di premio. Di conseguenza avranno le
stessa tempistica del pagamento premi
per spese di gestione: si tratta di spese non direttamente imputabili al
singolo contratto. Generalmente a ciascun contratto viene assegnata una
quota annua di spese pari a una fissata aliquota del capitale assicurato
Premio equo e base tecnica del rischio
• Le imprese di assicurazione sono caratterizzate da un inversione del ciclo
produttivo: infatti viene pagato anticipatamente un premio a fronte di una
prestazione futura collegata al verificarsi di un determinato evento.
• Di conseguenza l’ipotesi più semplice è la seguente:
Non si verifica l’evento assicurato
•
Premio Unico
o sequenza di premi
Si verifica l’evento
assicurato
Non vi è alcuna
prestazione
Pagamento del
Capitale Assicurato
Quindi fissato il capitale assicurato, per il calcolo del premio occorrerà tener
conto della probabilità di verificarsi dell’evento e dei rendimenti finanziari
derivanti dal fatto che intercorre un orizzonte temporale tra il momento di
incasso del premio e l’istante in cui viene erogata la prestazione.
IL PREMIO
nelle assicurazioni contro i danni
Il premio:
premio equo, premio puro, premio di tariffa
• Un contratto di assicurazione contro i danni prevede il pagamento di
un premio
in un’unica soluzione
(all’epoca di stipulazione del contratto)
rateizzato nel periodo di copertura
(supposto di durata annuale)
¾ Premio equo: valore atteso del risarcimento globale a
carico dell’assicuratore nel periodo di copertura
¾ Premio puro (o, anche, premio netto): corrispettivo del
risarcimento globale trasferito a carico dell’assicuratore
¾ Premio di tariffa (o, anche, premio commerciale): importo
richiesto dall’assicuratore a fronte della stipulazione del contratto
Caricamento di sicurezza e premio puro
Premio
equo
+
Caricamento
di
sicurezza
=
Premio
puro
- introdotto per fronteggiare la rischiosità
dell’operazione assicurativa
- eguale al valore atteso del guadagno che
l’assicuratore consegue in relazione al contratto
Caricamento per spese e premio di tariffa
Premio
puro
+
Caricamento
per
spese
=
Premio
di tariffa
- introdotto allo scopo di coprire le varie spese
sostenute dall’assicuratore in relazione al
contratto
9 Il premio effettivamente pagato dal contraente
(prezzo della copertura assicurativa)
è ottenuto sommando al premio di tariffa le tasse e gli eventuali
altri contributi che gravano sul contratto
Il calcolo del premio equo
• METODOLOGIE DI CALCOLO
¾ APPROCCIO TEORICO: fondato sull’individuazione di un
opportuno modello per la descrizione della base tecnica del rischio
(distribuzione di probabilità del risarcimento globale X) nell’ambito di un
portafoglio di rischi analoghi
¾ APPROCCIO EMPIRICO: fondato sull’osservazione di un
opportuno portafoglio di contratti assicurativi registrando, per
ciascuno di essi, i sinistri accaduti (e denunciati) ed i relativi danni e
risarcimenti
Il calcolo del premio equo
L’APPROCCIO TEORICO (1/2)
P = E ( X ) = E ( N ) E (Y )
valore atteso del risarcimento globale
a carico dell’assicuratore nel periodo di copertura
(nelle ipotesi classiche della teoria del rischio precedentemente formulate)
in media si ottiene l’equilibrio tra le entrate (introito del premio equo)
e le uscite (pagamento dei risarcimenti per sinistri)
Il calcolo del premio equo
L’APPROCCIO TEORICO (2/2)
EFFETTO MUTUALISTICO:
trasferimento di risorse finanziarie, all’interno di un dato
portafoglio di rischi analoghi, tra rischi sinistrati e
rischi non sinistrati
- Aspetto caratteristico dell’attività assicurativa
Permette di realizzare, in media, l’equilibrio tra le entrate e le uscite
Il calcolo del premio equo
L’APPROCCIO EMPIRICO (1/2)
Il premio equo viene valutato mediante un’opportuna
osservazione statistica
Portafoglio di rischi analoghi (a quello in esame) con riferimento:
a) alle caratteristiche del rischio adeguatamente valutabili,
all’epoca di stipulazione del contratto, da parte dell’assicuratore
b) alle condizioni contrattuali di copertura
c) ai valori monetari di esposizione al rischio (ad esempio i valori
dei beni assicurati o i massimali di garanzia)
In riferimento ad una durata annuale
Il calcolo del premio equo
L’APPROCCIO EMPIRICO (2/2)
¾ Quota risarcimenti (impropriamente detta quota danni)
danni
y1 + y2 + ... + ym
Q=
R
numero (sufficientemente grande)
di rischi presenti nel portafoglio
y1, y2 ,..., ym singoli risarcimenti relativi ad ognuno degli m
sinistri che si suppone avere osservato nel periodo di riferimento
Premio equo osservato
La scomposizione del premio equo osservato
⎛m⎞
Q=⎜ ⎟ y
⎝R⎠
INDICE DI SINISTROSITÀ
(impropriamente detto frequenza di sinistro):
numero medio di sinistri relativi ad un rischio
risarcimento
medio relativo
ad un sinistro
Q:
IMMAGINE STATISTICA DEL PREMIO EQUO
indice di sinistrosità, ψ,
stima del valore atteso, E(N),
del numero di sinistri
risarcimento medio relativo ad un sinistro, y ,
stima del valore atteso, E(Y), del
singolo risarcimento
La scomposizione dell’indice di sinistrosità
⎛ R1 + 2 R2 + ... + hRh ⎞ ⎛ R − R0 ⎞
⎟⎟ ⎜
ψ = ⎜⎜
⎟ = ξϕ
⎝ R1 + R2 + ... + Rh ⎠ ⎝ R ⎠
indice di ripetibilità:
numero medio di
sinistri relativi ad un
rischio sinistrato
frequenza dei rischi
sinistrati
Ri (i=0,1,…,h): numero di rischi colpiti da ‘i’ sinistri
h: numero massimo di sinistri rilevati in relazione ad almeno
uno dei rischi osservati
Esposizione monetaria al rischio e
tasso medio di premio (equo)
Nel caso più realistico di diverse esposizioni monetarie al rischio:
y1 + y 2 + ... + y m
τ=
w1 + w 2 + ... + w R
esposizioni monetarie relative
ad ognuno degli ‘R’ rischi
osservati
Tasso medio di premio
in breve detto
Tasso di premio
Premio equo osservato
In riferimento ad
un’unità monetaria di
esposizione
La scomposizione del tasso medio di premio
⎛m⎞ ⎛ y ⎞
τ =⎜ ⎟ ⎜ ⎟
⎝R⎠ ⎝w⎠
Indice di
sinistrosità
grado medio di risarcimento
(impropriamente detto grado medio di danno):
rapporto (adimensionale) esprimente il
risarcimento medio per unità monetaria di
esposizione
9 RELAZIONE TRA PREMIO EQUO E TASSO MEDIO DI PREMIO:
Nel caso in cui w1 = w2 = … = wR = w è immediata la relazione
P = τw
tra il premio equo, P, ed il tasso di premio,τ
(copertura assicurativa caratterizzata da eguale esposizione monetaria al rischio)
Caricamento di sicurezza e premio puro
• Guadagno:
G =Π− X
importo aleatorio eguale alla differenza
tra il premio incassato, Π, ed il risarcimento globale X
Il premio equo, P = E(X), è quel particolare premio che
rende nullo il guadagno atteso per l’assicuratore
Π=P
⇒
E (G ) = P − E ( X ) = 0
Principio di calcolo del premio detto principio di equità
Il principio di equità
privo di interesse economico:
non consente all’assicuratore di conseguire un guadagno atteso positivo
al momento della stipulazione del contratto
L’assicuratore è disponibile ad accettare la copertura del rischio solo se
Π > E(X)
Π = E( X ) + r
r = E(G) > 0
caricamento di sicurezza
Il premio puro
• Premio ottenuto sommando al premio equo un
caricamento di sicurezza
• Anche detto premio netto poiché determinato al netto
del corrispettivo per le spese che l’assicuratore sostiene
in relazione al contratto.
GIUSTIFICAZIONE TEORICA:
a) criterio della probabilità di rovina, nell’ambito della
teoria del rischio
b) criterio dell’utilità attesa, nell’ambito della teoria del
comportamento di un soggetto economico in condizioni di incertezza
Il criterio della probabilità di rovina
• Teorema della rovina del giocatore:
i.
se un giocatore (ad esempio l’assicuratore)
dispone di una data ricchezza iniziale
ed affronta, in condizioni di equità,
una sequenza potenzialmente infinita di partite contro
un avversario infinitamente ricco (ad esempio la massa degli assicurati),
essendo i risultati delle singole partite indipendenti
ed identicamente distribuiti,
allora
è certa la rovina del giocatore
(vale a dire, la perdita della ricchezza iniziale).
ii. se invece, ceteris paribus, le singole partite prevedono
un guadagno atteso positivo per il giocatore,
allora la rovina non è un evento certo
(probabilità di rovina del giocatore funzione decrescente - in particolare,
di tipo esponenziale - del guadagno relativo alla singola partita)
Il criterio dell’utilità attesa
¾ l’assicuratore, soggetto economico tipicamente avverso al rischio,
giudica vantaggiosa l’operazione assicurativa soltanto nell’ipotesi che il
premio sia maggiore del valore atteso di X
¾ l’assicurato, anch’egli soggetto economico tipicamente avverso al
rischio, giudica vantaggiosa l’operazione assicurativa malgrado
malgrad la non
equità del relativo prezzo
L’operazione assicurativa può così essere vantaggiosa per entrambe
le parti contraenti
per l’assicuratore,
grazie al caricamento
di sicurezza
per l’assicurato,
malgrado il caricamento
di sicurezza
Il caricamento di sicurezza
l’adozione di un caricamento di sicurezza nel premio ha lo scopo di
fronteggiare la rischiosità dell’operazione assicurativa
la dimensione del caricamento è legata ad un’opportuna
misura di questa rischiosità (varianza, scarto quadratico medio, …)
implicito
• Caricamento di sicurezza
esplicito
IL caricamento di sicurezza implicito
Generalmente praticato nelle assicurazioni sulla vita
¾ Introdotto mediante l’adozione, ai fini del calcolo del premio equo,
di una base tecnica favorevole all’assicuratore
(base tecnica prudenziale)
Essa è anche detta base tecnica di primo ordine.
ordine
E′(X) < E(X)
valutazione realistica che
l’assicuratore attribuisce
al risarcimento globale X
il premio (equo) P è in grado
di garantire all’assicuratore
un guadagno atteso positivo
E ′(G ) = E ( X ) − E ′( X ) > 0
Il caricamento di sicurezza esplicito
Usuale nelle assicurazioni contro i danni
¾ Commisurato ad uno o più valori caratteristici
(varianza, percentili, …) della distribuzione di probabilità
del risarcimento globale X
9 Talvolta al caricamento esplicito si aggiunge un caricamento implicito
ottenuto mediante l’adozione, ai fini del calcolo del premio equo,
di una base tecnica prudenziale (relativa al numero di sinistri e/o al danno).
Il calcolo del premio puro (1/2)
Π = H(X )
principio di calcolo del premio puro:
funzionale che associa un numero reale (il premio puro)
alla distribuzione di probabilità di X
(rappresentativa del rischio oggetto della copertura assicurativa)
il premio puro dipende, in generale, dalla funzione di ripartizione di X
Il calcolo del premio puro (2/2)
¾ I più importanti principi di calcolo del premio puro sono
funzione solamente dei principali valori caratteristici della
distribuzione di probabilità di X
Scarsità di basi statistiche attendibili
adottare un principio di calcolo che non richieda la
conoscenza dei momenti di ordine superiore al secondo
relativamente alla distribuzione di probabilità di X
9 Rischi assicurabili:
il funzionale H può non essere definito o può assumere valore infinito per
alcuni rischi
in quest’ottica la scelta del principio di calcolo
del premio puro gioca un ruolo chiave
I principi di calcolo del premio puro
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
principio del valore atteso;
principio della varianza;
principio dello scarto quadratico medio;
principio dell’utilità attesa;
principio del percentile;
principio del massimo danno probabile;
principio di Esscher;
principio di Orlicz;
principio di Wang.
Il principio del valore atteso
Π = (1 + α ) E ( X )
α>0
adimensionale
PROPRIETÀ:
inadeguatezza rispetto all’obiettivo prefissato
(la rischiosità del contratto non è opportunamente sintetizzata dal valore atteso di X )
semplicità di calcolo
(talvolta utilizzato nella pratica assicurativa)
Il principio della varianza
Π = E ( X ) + β var( X )
β>0
di dimensione eguale al
reciproco di un importo
PROPRIETÀ:
il caricamento di sicurezza è proporzionale alla rischiosità del
contratto misurata mediante la varianza di X
(la varianza è un buon indicatore della rischiosità di una variabile aleatoria)
frequentemente impiegato nella pratica assicurativa
Caricamento per spese e premio di tariffa
Le spese vengono imputate all’assicurato mediante un
caricamento per spese
Premio di tariffa
(o, anche, premio commerciale)
C =Π+s
Al premio puro si aggiunge il
caricamento per spese
9 L’incidenza percentuale del caricamento per spese sul premio di
tariffa (“expense ratio”) dipende fortemente dalle caratteristiche del
rischio assicurato
Caricamento per spese
• Decomposizione del caricamento per spese
s = s1 + s2
caricamento globale relativo
alle spese di acquisizione del
contratto e di incasso premi
(a) e (b)
caricamento relativo alle
spese generali di gestione
(c)
9 Nel caso in cui il caricamento per spese venga quantificato mediante il
principio di equità, l’ammontare del caricamento, (per ciascuna categoria di
spese), è eguale al valore atteso delle spese medesime, determinato secondo
una valutazione realistica.
9 Nella pratica assicurativa viene in genere adottato un margine implicito di
caricamento per spese a favore dell’assicuratore (ipotesi prudenziale sulle spese)
La dimensione è generalmente modesta (per lo più, non superiore al 3-4%).
La giustificazione risiede nell’aleatorietà connessa alle spese che l’assicuratore
sostiene in relazione al contratto (usualmente modesta)
IL PREMIO
nelle assicurazioni sulla vita
Base tecnica e premio equo (1/2)
T
⎡
⎤
−t
Ρ
Ε ⎢ ∑ Ft (1 + i ) ⎥
⎢⎣t = 0
⎥⎦
RISCHIO DEMOGRAFICO
RISCHIO FINANZIARIO
Base tecnica e premio equo (2/2)
T
T
⎤
⎡
−t
−t
Ρ
VAA = Ε ⎢ ∑ Ft (1 + i ) ⎥ = ∑ Ft (1 + i ) ⋅ pt
⎥⎦ t = 0
⎢⎣t = 0
• Il calcolo del valore attuale atteso (VAA) richiede
l’introduzione di un modello probabilistico. Nel caso delle
assicurazioni sulla vita, il modello riguarda la durata
aleatoria della vita dell’assicurato.
Il premio assicurativo
Il calcolo dei premi assicurativi è determinato in funzione
di due elementi unilateralmente fissati dalla Compagnia di
Assicurazione:
– Un modello probabilistico;
– Una struttura dei tassi.
VAA =
T
−t
(
)
F
1
+
i
⋅ pt = PREMIO
∑ t
t =0
Il guadagno atteso
• Il premio calcolato con un tasso i, pari a quello ottenuto
dall’investimento del premio, e con una probabilità p, pari alla
probabilità di sopravvivenza che la Compagnia attribuisce
all’assicurato, porta alla determinazione del premio equo.
• Il premio equo, secondo la base tecnica di primo ordine deve
risultare “favorevole” all’assicuratore.
Ε P [Π(i )] > 0
• La coppia (i, p) va rivista in termini (i*, p*), con l’obiettivo di
analizzare il guadagno atteso.
La scelta della base tecnica
• La coppia (i, p), impiegata per il calcolo del premio, è detta
base tecnica di primo ordine
• La nuova coppia (i*, p*), che esprime uno scenario
demografico-finanziario più realistico, è detta base tecnica
di secondo ordine
• Il tasso di interesse adottato nella base tecnica può essere
estratto da una struttura per scadenze piatta o dinamica.
• La probabilità deriva da un modello probabilistico a tempo
discreto o continuo.
• Ipotesi semplificatrice: tasso costante e tempo discreto.
Premi unici o premi periodici
IL PRINCIPIO DI EQUITÀ
Il valore attuariale delle prestazioni corrisponde al
PREMIO UNICO PURO
[]
~
Ε Y = PU
Il concetto di equità è strettamente legato alla base tecnica
adottata. L’uso di una base tecnica “realistica” comporterebbe un
guadagno atteso nullo e un significativo rischio di perdite.
Premi periodici
• Controprestazione ripartita tra più rate, costanti o variabili,
pagate ad intervalli regolari (anni, mesi,…).
• Pagamento anticipato, con inizio all’epoca di stipulazione e
per un tempo non superiore alla scadenza del contratto.
• L’importo assicurato e i premi periodici rappresentano le rate
di ammortamento demografico-finanziario del premio unico.
• Il pagamento di premi periodici, al contrario del premio unico,
è subordinato alla sopravvivenza del soggetto assicurato.
POSSIBILI ESEMPI:
- Premi variabili
- Premi costanti
- Premi unici ricorrenti
Premi unici ricorrenti
• Tipici dei contratti assicurativi a prestazioni differite
(capitale differito, rendite differite, caso morte differita).
• Costituiscono una forma di “piano previdenziale” a mediolungo termine.
• I versamenti periodici garantiscono l’acquisto di una quota
di polizza.
• Il capitale assicurato è noto solo alla fine di tutti i
versamenti.
Premi naturali
• Obiettivo: il frazionamento del premio unico deve, in ogni
periodo, garantire la copertura degli impegni assunti dalla
Compagnia.
• Analisi: confronto tra l’introito dei premi (in genere costanti) e
il profilo temporale dei costi annui attesi.
• Problema: sottofinanziamento.
• Strumento: PREMIO NATURALE
Singolo premio commisurato al valore atteso
degli impegni della Compagnia,
in ciascun periodo del frazionamento preso in esame.
Caricamento di sicurezza
Differenza tra il premio puro adottato e
il premio equo calcolato con la base realistica.
Il caricamento può essere:
• IMPLICITO: determinato dall’uso di basi tecniche più
“favorevoli” all’assicuratore
• ESPLICITO: dato da una specifica maggiorazione applicata al
premio equo.
Premio di tariffa
• Rappresenta l’esborso effettivo del contraente, cioè copre il
premio puro e le spese: di acquisizione, di incasso, di gestione,…
• Il caricamento può essere:
– Proporzionale al capitale assicurato, hC,
– Proporzionale al premio puro, HP, o al premio di tariffa HPT,
– Parte in percentuale del capitale assicurato e parte in
percentuale del premio puro o di tariffa.
PT = P + hC + HP
oppure
PT = P + hC + HPT
Analogamente per
il premio unico
Le riserve tecniche
considerazioni generali
Le riserve tecniche
• Le riserve tecniche servono a far fronte allo sfasamento
temporale delle prestazioni tipico del ciclo assicurativo.
• Con i premi incassati l’assicuratore deve gestire il contratto nel
corso della sua durata………..
• ………. per farlo deve accantonare risorse da cui poter attingere
al momento di necessità.
• Tali accantonamenti sono imposti per legge (dal Codice Civile)
al fine di tutelare gli assicurati dal rischio di insolvenza
dell’assicuratore.
• Le riserve tecniche sono vincolate, regolarmente valutate e
controllate dagli organi di Vigilanza e non possono essere
liberamente investite sul mercato.
Le riserve tecniche
nelle assicurazioni contro i danni
Le riserve tecniche
¾ Le riserve tecniche, con il cui termine vengono indicate
sia la riserva premi che la riserva sinistri, costituiscono un
debito dell’assicuratore nei confronti dell’assicurato
CONTRADDISTINDE DALLE
RISERVE PATRIMONIALI
fondi liberi da impegni gestionali e pertanto
quantità a disposizione dell’impresa
9 Sostanzialmente si formano mediante accantonamento di utili e sono
utilizzate per fronteggiare altri obblighi di gestione e non quelli tecnici
Quadro legislativo italiano (1/2)
D.L. 175/’95
L’articolo 23 del D.L. 175/’95 dichiara:
1.
“Le imprese di assicurazioni che svolgono la loro attività nei rami danni
devono costruire la riserva dei premi per i rischi che sono in corso alla fine
di ogni esercizio, iscrivendo nel bilancio l’importo delle frazioni di premio
di competenza degli esercizi successivi e quello delle annualità dei premi
pagati anticipatamente per gli anni futuri…” (Relativamente alla riserva
premi).
2.
Le imprese debbono inoltre costruire alla fine di ogni anno di esercizio la
riserva sinistri, iscrivendo nel bilancio l’ammontare complessivo delle
somme che, da una prudente valutazione effettuata…, risultino necessarie
per far fronte al pagamento dei sinistri avvenuti…e non ancora
liquidati…” (Relativamente alla riserva sinistri).
3.
La riserva per rischi in corso deve essere calcolata con il metodo prorata-temporis…” (Relativamente alla valutazione della riserva premi).
Quadro legislativo italiano (2/2)
D.L. 175/’95
Con l’articolo 26 viene introdotta l’obbligatorietà di
costituire anche la riserva per sinistri IBNR
“le imprese di assicurazione hanno l’obbligo di
costituire…una riserva per i sinistri avvenuti
nell’esercizio, ma non ancora denunciati al termine
dell’esercizio stesso…”
¾ Con il successivo decreto legislativo 173/’97 sono poi
apportate alcune modifiche………
La riserva premi
Riserva per frazioni di premio
Riserva per rischi in corso
utilizzata per coprire quei
rischi i cui premi sono
già stati incassati, ma la
cui durata va oltre la
chiusura di esercizio
considera il rapporto
sinistri/premi (loss ratio) ed è
utilizzata a valutarne la sua
capacità di far fronte al rischio
assicurato durante l’intera
copertura contrattuale
La gestione del premio (1/2)
¾ Si consideri un portafoglio di contratti
sufficientemente omogenei in base a quanto sia
possibile affermare al tempo 0
- Tutti i contratti vengono stipulati al tempo 0
- Tutti i contratti sono di durata annuale
- Il tempo 0 coincide con l’epoca di avvio dell’attività assicurativa
Al tempo 0 l’assicuratore incassa un premio (somma dei
premi di tariffa complessivi) comprensivo dei vari caricamenti
C = ε1C + ε 2C
caricamento per spese
di acquisizione
caricamento per spese
di gestione
9 La terza componente
(spese di liquidazione dei sinistri),
si considera compresa nell’entità
dei risarcimenti, X
La gestione del premio (2/2)
Con l’ulteriore condizione di spese di gestione uniformemente
distribuite nel corso dell’anno
d (t ) = C (t ) − X (t )
ammontare complessivo
dei premi che restano a
disposizione all’epoca t
Disponibilità all’epoca t
importo dei risarcimenti
complessivamente
cumulato da 0 a t
d (t ) = C (t ) − X (t ) = C − ε1C − tε 2C − X (t ) =
= C (1 − ε 1 − tε 2 ) − X (t ).
La gestione del premio: riserva premi
¾ La disponibilità all’epoca t non rappresenta il
guadagno dell’assicuratore al tempo t
Tra t ed 1, infatti, la compagnia di assicurazione dovrà sostenere
ulteriori uscite, sia per spese di gestione che per i relativi
risarcimenti; mentre le entrate saranno pari a 0
All’epoca t, ci sono ancora impegni futuri che l’assicuratore
detiene nei confronti degli assicurati e che devono essere calcolati
sulla base della suddetta disponibilità
RISERVA PREMI
Riserva premi
Se si assume che anche gli oneri avvengano con continuità ed
uniformità nel corso dell’anno
RISERVA PREMI
R p (t ) = (1 − t )(1 − ε 1 )C
9 Si osservi che, al tempo 0, all’assicuratore resta a disposizione
C (1- ε1) per fare fronte alle spese di gestione e di liquidazione
sinistri poiché il caricamento C ε1 è interamente utilizzato in 0
per le spese di acquisizione dei contratti
• Guadagno al tempo t
g (t ) = d (t ) − R p (t )
Guadagno
• Guadagno al tempo t
g (t ) = d (t ) − R p (t )
• Guadagno alla scadenza dei contratti
g (1) = d (1) = C (1 − ε1 − ε 2 ) − X (1)
¾ Ovviamente il guadagno in 1 può essere maggiore, minore,
o uguale a 0, a seconda che gli esborsi complessivi, X(1) ,
risultino, rispettivamente, inferiori, superiori, o uguali al
premio puro al tempo 1, dato da C (1- ε1 - ε2)
Metodi di valutazione per la riserva premi
¾ La valutazione della riserva premi avviene all’epoca di
bilancio (che in genere coincide con la fine dall’anno solare)
¾ La stima si basa sulla durata media residua dei
contratti assicurativi
• Ai fini dei calcoli, esistono due approcci:
a) Metodo sintetico o forfettario
b) Metodo individuale o pro-rata-temporis
Metodi di valutazione per la riserva premi
METODO SINTETICO O FORFETTARIO
¾ Esso consiste nell’individuare un’unica durata residua
media a partire dalle ‘m’ durate residue, tj + 1 - t,
relative ai singoli contratti
• Per farlo si sintetizza gli ‘m’ valori effettuandone una media
Ipotizzando uniforme distribuzione nell’incasso premi
m
R p (1) = ∑ t j (1 − ε 1 )C j ≈
j =1
≈
1
(1 − ε 1 )C j
2
Sostanzialmente, le ‘m’ durate
residue sono state sintetizzate in
un’unica durata media residua
posta pari a metà anno
t=
1
2
Metodi di valutazione per la riserva premi
METODO INDIVIDUALE O PRO-RATA-TEMPORIS
(1/2)
¾ Se si utilizza questo metodo vengono invece considerate
tutte le durate residue relative ad ogni singolo contratto
stipulato dall’assicuratore
sono esaminati tutti gli ‘m’ contratti senza alcuna aggregazione
• Nello specifico, viene individuata un’unità di misura di tempo
rispetto alla quale calcolare la durata residua relativamente ad
ognuno degli ‘m’ contratti
Metodi di valutazione per la riserva premi
METODO INDIVIDUALE O PRO-RATA-TEMPORIS
(2/2)
¾ L’unità di misura presa a riferimento può essere:
a) Il mese
Metodo dei 12-esimi
b) Il mezzo mese
Metodo dei 24-esimi
c) Il giorno
Metodo dei 365-esimi
Metodi di valutazione per la riserva premi
METODO INDIVIDUALE O PRO-RATA-TEMPORIS
a) Metodo dei 12-esimi
ESEMPIO
Se l’unità di misura è il mese, nell’anno che si è appena
concluso e per un contratto stipulato il 22 ottobre
risultano essere state coperte 3 unità (mesi);
mentre ne restano fuori le rimanenti 9
Posto (1 − ε 1 )C j = 100
9
R p (1) = 100 ⋅
12
Metodi di valutazione per la riserva premi
METODO INDIVIDUALE O PRO-RATA-TEMPORIS
b) Metodo dei 24-esimi
ESEMPIO
Se l’unità di misura è il mezzo mese, nell’anno che si è
appena concluso e per un contratto stipulato il 22 ottobre
risultano essere state coperte 5 unità (mezzo mese);
mentre ne restano fuori le rimanenti 19
Posto (1 − ε 1 )C j = 100
19
R p (1) = 100 ⋅
24
Metodi di valutazione per la riserva premi
METODO INDIVIDUALE O PRO-RATA-TEMPORIS
c) Metodo dei 365-esimi
ESEMPIO
Se l’unità di misura è il giorno, nell’anno che si è appena
concluso e per un contratto stipulato il 22 ottobre
risultano essere state coperte 70 unità (giorni);
mentre ne restano fuori le rimanenti 295
Posto (1 − ε 1 )C j = 100
295
R p (1) = 100 ⋅
365
Metodi di valutazione per la riserva premi
OSSERVAZIONI
1) Osserviamo che i 3 metodi ammettono risultati diversi:
in particolare si conseguono valori crescenti
9 In genere, viene utilizzato il secondo metodo, quello
dei 24-esimi
2) Il metodo individuale o pro-rata-temporis fornisce una
stima esatta della riserva premi nel caso di uniforme
distribuzione degli impegni nel corso del tempo;
mentre il metodo sintetico o forfetario è in grado di
fornire solo una stima molto approssimata
3) Il pro-rata-temporis è di facile applicazione con
l’utilizzo di calcolatori elettronici, sebbene implichi
un certo costo
La riserva per rischi in corso
D.L. 173/’97
¾ RISERVA PER RISCHI IN CORSO
consente una visione globale della posizione assicurativa
ed i futuri risarcimenti sono confrontati con le
quote di premio già incassate più le rate che verranno
corrisposte in seguito dall’assicurato
S
P
×
Riserva per
frazioni di premio
+
Rate di premio
a scadere
(-)
“loss ratio”
rapporto
sinistri/premi
Riserva per
frazioni di premio
+
Rate di premio
a scadere
L’evoluzione dei sinistri e la riserva sinistri
¾ Per quanto analizzato fino adesso, i sinistri risultano
essere immediatamente denunciati, registrati e liquidati
nel momento stesso in cui essi avvengono
EVOLUZIONE DI UN SINISTRO
non registrato
t
epoca di
accadimento
t+s
epoca di
denuncia e
registrazione
aperto
liquidato
t+s+r
epoca in cui è definito
l’ammontare del
risarcimento
chiuso
L’evoluzione dei sinistri e la riserva sinistri
¾ Esiste dunque un ulteriore debito che l’assicuratore detiene
nei confronti degli assicurati.
È necessaria una ulteriore riserva tecnica
RISERVA SINISTRI
al fine di adempiere a quei risarcimenti relativi a sinistri
già avvenuti, ma per i quali non è stato effettuato
ancora alcun pagamento, o lo è stato fatto solo in parte
Riserva sinistri
¾ Nello specifico, la riserva sinistri è costituita da due elementi:
- il primo attinente a quei sinistri registrati, ma non ancora
pagati o pagati solo in parte, detta riserva IBNER
- il secondo relativo a quei sinistri non ancora registrati,
detta riserva IBNR
IBNER
(Incurred But Not Enough Reserved):
Riserva Sinistri
sinistri registrati ma non ancora pagati
o pagati solo in parte
IBNR
(Incurred But Not Reported):
sinistri non registrati
Riserva sinistri e guadagno
¾ Considerando anche la riserva sinistri
• Guadagno al tempo t
g (t ) = d (t ) − R p (t ) − Rs (t )
• Guadagno alla scadenza dei contratti
g (1) = d (1) − Rs (1)
9 È interessante osservare che il guadagno in 1 non è più un
valore certo, così come lo era in presenza della sola riserva premi:
- la stima della riserva sinistri lo rende infatti una quantità stimata.
Metodi di valutazione per la riserva sinistri
ALCUNE CONSIDERAZIONI (1/2)
¾ Analizziamo in dettaglio i due elementi che
individuano la riserva sinistri
- la riserva IBNER viene utilizzata
per risarcire quei sinistri
denunciati e registrati, ma non
ancora definitivamente chiusi.
comprende i
sinistri aperti ed
i liquidati
- la riserva IBNR, serve a risarcire
le cosiddette tardive denunce, ossia
quei sinistri che all’epoca di
valutazione sono già avvenuti, ma
non sono ancora stati denunciati
comprende i
sinistri non
registrati
(TARDIVE DENUNCE)
Metodi di valutazione per la riserva sinistri
ALCUNE CONSIDERAZIONI (2/2)
1) Da un punto di vista assicurativo, è facilmente
comprensibile la maggiore importanza della
componente IBNER.
(La riserva IBNR riguarda infatti un numero piccolo di sinistri,
verificatisi in prossimità della data di valutazione)
2) Da un punto di vista riassicurativo, le tardive denuncie
conseguono non solo da parte degli assicurati nei confronti
degli assicuratori diretti; bensì, anche e soprattutto, da parte
degli assicuratori diretti nei confronti dei riassicuratori
Metodi di valutazione per la riserva sinistri
(1/2)
¾ La stima della riserva sinistri è in genere effettuata alla
fine di un certo anno solare (ossia ad un 31/12)
• Esistono due approcci di stima:
a) Metodo collettivo o sintetico
si basa su una collettività di rischi il più possibile
omogenei tra loro
b) Metodo individuale o analitico
considera ogni singolo sinistro e lo segue nel
tempo in un ottica di monitoraggio
Metodi di valutazione per la riserva sinistri
(2/2)
¾ Vantaggi e svantaggi dei due approcci
- dipendono dalle caratteristiche del portafoglio
assicurativo
1) Se l’assicuratore ha a disposizione un portafoglio con un
numero sufficientemente grande ed omogeneo di rischi,
caratterizzato da risarcimenti di importo medio-basso,
l’approccio collettivo è in grado di dare buoni risultati
a) necessità anche di stabilità, ossia dovrebbero restare
costanti nel tempo le modalità di liquidazione dei sinistri,
così come i relativi costi
2) L’approccio individuale, invece, risulta opportuno in
presenza di pochi sinistri ma molto onerosi
Metodi di valutazione per la riserva sinistri
APPROCCIO COLLETTIVO (1/5)
ANNO DI DIFFERIMENTO
0
1
.
.
.
.
0
ANNO
DI
DENUNCIA
1
.
.
.
.
γ ij
γˆij
k
¾ Base di partenza
.
k
k+1
Metodi di valutazione per la riserva sinistri
APPROCCIO COLLETTIVO (2/5)
- k: numero massimo di anni in cui si presuppone
completare il pagamento di ogni singolo sinistro
coincide anche con l’anno corrente, (al momento il 2007);
- il tempo 0 comprende anche tutti quei sinistri che non sono
stati chiusi nel periodo k prestabilito, sebbene questi non
siano molti (circa un 1%,2%), nel caso in cui il valore di k
sia stato scelto adeguatamente
La loro entità complessiva è supposta nota ed è
espressa con R0,k+1
Metodi di valutazione per la riserva sinistri
APPROCCIO COLLETTIVO (3/5)
¾ Lettura della tabella
- per riga troviamo l’evoluzione di una generazione di
sinistri rispetto alle epoche in cui vengono effettuati i
risarcimenti
- per colonna abbiamo il trend negli anni di differimento: come si
comportano le varie generazioni dei sinistri relativamente ad un dato
anno di differimento.
Ad esempio, un trend decrescente all’interno di una colonna,
corrisponde ad un anno in cui i risarcimenti diminuiscono nel corso del tempo
- sulla diagonale sono presenti i pagamenti relativi all’anno di
valutazione
Metodi di valutazione per la riserva sinistri
APPROCCIO COLLETTIVO (4/5)
¾ Stime
la diagonale suddivide la tabella in due triangoli
- un triangolo superiore, dove si trovano gli elementi
noti, la base statistica a disposizione
- un triangolo inferiore, dove verranno inserite le
stime future
Le stime, ed in conseguenza le quantità a disposizione per
effettuarle, possono basarsi su
γ ij
Yij risarcimenti non cumulati relativi alla
generazione i, con j anni di differimento
Xij risarcimenti cumulati relativi alla generazione i, e
risarciti al massimo entro j anni di differimento
Metodi di valutazione per la riserva sinistri
APPROCCIO COLLETTIVO (5/5)
• OSSERVAZIONI
1) Le considerazioni effettuate fanno riferimento ai sinistri liquidati:
- l’analisi esclude i sinistri aperti, che dovranno poi essere inseriti
nel costo complessivo
2) I dati della base statistica derivano o proprio dalla compagnia di
assicurazione o da un gruppo di compagnie.
- I problemi maggiori riguardano i riassicuratori, i quali sono costretti a
svolgere i loro calcoli sulla base di dati molto incompleti
3) Per avere una stima della riserva IBNR basterebbe considerare
l’anno di accadimento, anziché quello di denuncia
Approccio collettivo
METODI DI STIMA (1/4)
¾ Le stime che devono essere individuate sono
- γˆ ij che può rappresentare o i singoli risarcimenti o i risarcimenti
cumulati
- Rˆ i ,k +1 che determina quei sinistri che appartengono alla generazione
i e che non vengono risarciti in k anni di differimento
Le ipotesi dell’approccio collettivo sono
a) una base statistica appropriata
b) la disponibilità di un modello di proiezione
Approccio collettivo
METODI DI STIMA (2/4)
¾ Metodi di proiezione
a) Metodi deterministici
forniscono una stima puntuale della riserva
b) Metodi stocastici
permettono di considerare l’aleatorietà del portafoglio
analizzato, creandone una stima intervallare entro la
quale la riserva sinistri si collocherà
9 Sono evidenti i vantaggi dei metodi stocastici, in grado
di fornire misure di variabilità della stima individuata ed il
conseguente livello di fiducia ad essa attribuita
Approccio collettivo
METODI DI STIMA (3/4)
¾ Metodi deterministici
- possono basarsi su 2 tecniche di proiezione distinte
a) “grossing up”
fa riferimento alla proporzione di risarcimenti effettuati
nel corso degli anni di differimento in rapporto al totale
⎛
⎜ Y
r0 = ⎜ i 0
⎜ ∑ Yij
⎝ j
⎞
⎞
⎛
⎟
⎜ Y ⎟
⎟; r1 = ⎜ i1 ⎟;
⎟
⎜ ∑ Yij ⎟
⎠
⎠
⎝ j
......
⎛
⎜ Y
rh = ⎜ ih
⎜ ∑ Yij
⎝ j
⎞
⎟
⎟;
⎟
⎠
......
Approccio collettivo
METODI DI STIMA (4/4)
¾ Metodi deterministici
b) “link ratio”
considera la proporzione dei risarcimenti effettuata nel corso
degli anni di differimento in rapporto all’anno precedente
⎛ Yi 2 ⎞
⎛ Yi1 ⎞
r0 = ⎜⎜ ⎟⎟; r1 = ⎜⎜ ⎟⎟;
⎝ Yi1 ⎠
⎝ Yi 0 ⎠
......
⎛ Yih +1 ⎞
⎟⎟;
rh = ⎜⎜
⎝ Yih ⎠
......
9 La logica è poi quella di moltiplicare gli elementi che si
trovano sulla diagonale, (valori più recenti a disposizione),
per i coefficienti, r0, r1,…, rh, a secondo della tecnica utilizzata
Approccio collettivo
RISERVA SINISTRI (1/2)
¾ Una volta individuate le stime relative agli elementi del
triangolo inferiore:
- l’entità della riserva sinistri è determinata semplicemente
sommando tutti questi valori;
- ed aggiungendo, inoltre, i termini aggiuntivi (anche questi stimati),
Ri,k+1, (i =1,2,…,k), relativi alle riserve per i pagamenti effettuati
con più di k anni di differimento
Approccio collettivo
RISERVA SINISTRI (2/2)
1) Nel caso di singoli risarcimenti γ ij = Yij
R
IBNER
(k )
⎛ k ˆ
⎞
= ∑ ⎜⎜ ∑ Yij + Rˆ i ,k +1 ⎟⎟ + R0,k +1
i =1 ⎝ j = k −i +1
⎠
k
2) Nel caso di risarcimenti cumulati γ ij = X ij
k
[(
)
]
ˆ −X
ˆ
R(IBNER
=
X
+
R
∑
k)
ik
ik − i
i , k +1 + R 0 , k +1
i =1
Metodo della catena (Chain-Ladder)
(1/4)
¾ Il metodo si basa sugli importi cumulativamente pagati
per sinistri della generazione i nei primi j anni di differimento, Xij
La tecnica di proiezione su cui si basa è quella
del “link ratio”
IPOTESI:
esiste una “legge di smontamento” dei sinistri
costante per ogni anno di generazione
- Tale legge rappresenta la progressione dei risarcimenti
cumulati nel corso degli anni di differimento
X 01 X 11 X 21
=
=
= ......
X 00 X 10 X 20
Metodo della catena (Chain-Ladder)
(2/4)
¾ I rapporti
X ij
non dipendono, a meno di variazioni
X ij −1
aleatorie, dall’anno di denuncia i, ma solo dall’anno di
generazione j
¾ Stima dei rapporti m j =
X ij
X ij −1
k− j
mj =
∑X
i =0
k− j
∑X
i =0
ij
ij −1
,
j = 1,2,..., k
Metodo della catena (Chain-Ladder)
(3/4)
¾ Una volta individuati tutti i coefficienti mi, (i =1,2,…k),
le stime sono facilmente calcolabili
Xˆ hz = X hk − h
z
Cm
j = k − h +1
h = 1,2,..., k
j
z = k − h + 1,..., k
¾ I termini aggiuntivi sono invece stimati con
Rˆ i ,k +1 = Xˆ ik m k +1
dove m k +1 =
X 0 k + R0,k +1
X 0k
Metodo della catena (Chain-Ladder)
(4/4)
• OSSERVAZIONI
1) In questo caso vengono considerati tutti i dati disponibili
relativi a due colonne consecutive
- esistono ulteriori versioni del metodo, le cui stime si
basano solo su alcuni dei dati a disposizione
2) Si può pensare di utilizzare i valori relativi solo agli
ultimi 3 o 5 anni di generazione oppure assegnare “pesi”
diversi alle quantità note
-il fine è quello di attribuire ai dati una importanza
diversa in base al loro riferimento temporale.
(Ad esempio, è plausibile ritenere più affidabili i dati più recenti)
Varianti del metodo della catena (1/5)
Le Ipotesi
A fronte dei pochi dati richiesti ai fini dei calcoli,
- il metodo presuppone anche l’ipotesi di costanza,
rispetto alle varie generazioni, della progressione dei
pagamenti cumulati
LIMITE
¾ Nel tempo può variare
- la gestione amministrativa dell’impresa in ambito
della liquidazione dei sinistri
- il comportamento della magistratura ed in
conseguenza i tempi di indennizzo
- ci sono poi gli effetti inflazionistici
Varianti del metodo della catena (2/5)
FATTORI “ESOGENI” E “TASSI INFLATIVI”
¾ È possibile attutire l’effetto dei cosiddetti fattori “esogeni”,
ossia esterni all’attività assicurativa,
introducendo tassi “inflativi” sulla base
delle osservazioni passate
• I “tassi inflativi” non corrispondono a quelli
ufficiali dell’inflazione economica:
- considerano anche gli effetti, diretti ed indiretti, sulla
gestione di impresa in ambito costi per risarcimenti
Varianti del metodo della catena (3/5)
¾ Procedimento operativo
I.
Il primo passo è quello di decomporre i risarcimenti
cumulati, per ogni anno di generazione, nei diversi
importi relativi ai singoli anni di differimento.
Si considerano le quantità Yij = X ij − X ij −1
II.
Si “inflazionano” poi questi valori prendendo come
anno di riferimento quello della generazione più recente
(nel caso il 2007) e si ottengono pertanto importi
“inflazionati”, Yij* , in euro 2007
j
III. Si ricostruiscono i risarcimenti cumulati, X ij∗ = ∑ Yiz∗ , e si
z =0
applica il classico metodo della catena a questi nuovi valori,
che, a questo punto, risultano espressi in euro 2007
Varianti del metodo della catena (4/5)
OSSERVAZIONE
¾ La stima non è ancora completa
Occorre considerare anche l’inflazione presente negli
anni futuri la valutazione
Si utilizza un procedimento analogo a quello
utilizzato per gli anni passati;
mentre il tasso di inflazione è ipotizzato essere costante
nel tempo ed è calcolato come una media
dei tassi riscontrati nel passato
Varianti del metodo della catena (5/5)
¾ Procedimento operativo per gli anni futuri la valutazione
IV. Si costruisce la matrice triangolare inferiore dei
pagamenti annuali previsti in futuro, che ricordiamo
essere espressi in euro 2007, Yˆij∗ = Xˆ ij∗ − Xˆ ij∗−1
V. Si “inflazionano” questi valori sulla base
dell’ipotesi di tasso costante precedentemente
effettuata
VI. La somma delle righe, (senza eventualmente ritornare
agli importi cumulati), rappresenta il valore della
riserva globale che, pertanto, considera sia l’inflazione
relativa agli anni passati, sia l’inflazione relativa agli
anni futuri.
Metodo dei minimi quadrati di De Vylder (1/4)
¾ Il metodo, creato da De Vylder nel 1978, si basa sul criterio
dei minimi quadrati
¾ I dati a disposizione sono i singoli importi relativi alla
generazione i risarciti con j anni di differimento Yij
• BASE STATISTICA
abbiamo a disposizione solo un insieme di informazioni parziali,
diciamo D, o per carenza di dati, o per loro inattendibilità
(i valori del triangolo superiore, quelli che costituiscono la base
statistica, non sono necessariamente tutti disponibili, oppure lo sono,
ma risultano inattendibili )
9 Aspetto molto diffuso anche nella realtà assicurativa
Metodo dei minimi quadrati di De Vylder (2/4)
IPOTESI:
il singolo risarcimento può essere fattorizzato in
Yij = p i r j
quantità che dipende dall’anno di
generazione i e ne esprime il
risarcimento complessivo
parametro adimensionale che dipende
dall’anno di differimento
e rappresenta la
“legge di smontamento dei sinistri”
9 La fattorizzazione è individuata a meno di una costante
moltiplicativa ed è univocamente determinata nel caso si assuma la
normalizzazione
k
∑r
j =0
j
=1
Metodo dei minimi quadrati di De Vylder (3/4)
La tecnica di proiezione su cui si basa è quella
del “grossing up”
¾ Le stime si ottengono secondo il criterio dei
minimi quadrati
∑ (Y
( i , j )∈D
ij
− pi rj )
insieme delle coppie (i,j)
effettivamente disponibili
2
Metodo dei minimi quadrati di De Vylder (4/4)
¾ Soluzioni
la soluzione, normalizzata, si ottiene utilizzando un
processo iterativo sulle quantità
∑Y r
=
∑r
ij j
a)
pi
j
2
j
; i = 1,2,..., k
Si parte da valori arbitrari assegnati
alle rj, (sotto la condizione ∑ r = 1 ),
da sostituire nell’ espressione (a)
per poi passare a calcolare la (b),
quindi ritornare alla (a), ……
e così via iterativamente
k
j
j
j =0
∑Y p
=
∑p
ij
b) rj
i
i
2
i
i
; j = 1,2,..., k
Alcune osservazioni sui metodi di stima (1/2)
1) La scelta dei metodi di stima da utilizzare ai fini dei calcoli
della riserva sinistri dipende molto dalle ipotesi su cui i
criteri si basano
- Il realismo delle ipotesi è spesso difficile da realizzare ed è
quindi difficile stabilire il metodo di valutazione appropriato
2) Criteri diversi possono apportare risultati di gran
lunga differenti
- In genere la stima viene effettuata utilizzando più metodi
di calcolo;
- il valore finale deriva poi da una media dei singoli
risultati ottenuti
Alcune osservazioni sui metodi di stima (2/2)
3) I modelli statistici possono essere controllati sfruttando,
con il passare del tempo, le informazioni passate, efficaci
elementi di confronto con le passate previsioni.
- Al riguardo, sarebbe invece auspicabile riferirsi ad uno stesso
modello di valutazione ed in conseguenza ai maggiori dati
disponibili nel corso del trascorrere dei diversi anni di esercizio
4) Comprensibile necessità di utilizzare modelli diversi per
portafogli con caratteristiche differenti.
5) L’importo finale della riserva sinistri (alla chiusura di un
esercizio) rappresenta una stima dell’impegno
complessivo dell’impresa nei confronti dei rischi
assicurati e non un suo valore attuale
Altre riserve tecniche (1/2)
¾ Riserve di perequazione
devono essere accantonate allo scopo di:
- perequare le fluttuazioni del tasso dei sinistri negli anni futuri;
- coprire rischi particolari.
• Riserva di compensazione
- deve essere costituita dalle imprese che operano nel ramo credito,
accantonando una percentuale dell’eventuale saldo tecnico positivo del ramo
secondo apposite modalità indicate nell’art. 80 del D.L. n.173 del 1997,
allo scopo di compensare i risultati (positivi e negativi) di più esercizi.
• Riserva di equilibrio per rischi di calamità naturali
- è prevista per tutti i rami danni, ad eccezione dei rami credito e cauzione,
e deve essere accantonata (secondo modalità stabilite con apposito decreto
ministeriale) allo scopo di compensare nel tempo l’andamento della sinistralità.
Altre riserve tecniche (2/2)
¾ Riserva di senescenza
- deve essere accantonata per quei contratti di assicurazione contro
le malattie con durata pluriennale e nei quali i premi sono calcolati
in base all’età dell’assicurato al momento della stipulazione del
contratto stesso;
- è destinata a compensare l’aggravarsi del rischio dovuto al
crescere dell’età degli assicurati;
- è calcolata su basi attuariali ma può anche essere calcolata
forfettariamente, in misura non inferiore al 10% dei premi lordi
dell’esercizio relativi ai contratti considerati.
¾ Riserve per partecipazioni agli utili e ristorni
- comprendono gli importi da attribuire agli assicurati o ai
beneficiari dei contratti a titolo di partecipazioni agli utili tecnici
e di ristorni.
Le riserve
nelle assicurazioni sulla vita
Le riserve matematiche
• L’articolo 36 del codice delle assicurazioni prevede per i contratti di
assicurazione sulla vita l’obbligo di costituire riserve tecniche sufficienti a
garantire le obbligazioni assunte e le spese future
• Secondo quanto previsto dall’art 25 del D.Lgs 174 l’impresa deve accantonare
una riserva matematica, calcolata, secondo un metodo attuariale prospettivo
sufficientemente prudente, utilizzando le stesse basi tecniche (di primo ordine)
adottate per il calcolo del premio.
• Per alcuni contratti assicurativi (collegati a fondi o a indici azionari) la riserva
dev’essere calcolata facendo riferimento ai valori di mercato.
• Le riserve calcolate tenendo contro delle prestazioni e dei premi puri, senza
considerare caricamenti di sicurezza e spese, vengono spesse definite riserve
matematiche pure.
• Tale voce, registrata nel passivo dello stato patrimoniale, esprime la
valutazione in un determinato istante dell’ammontare degli impegni futuri
nei confronti degli assicurati
La riserva matematica prospettiva
• Il decreto 174 prevede che la riserva venga calcolata con il metodo prospettivo:
la riserva esprime, cioè, la differenza tra il valore attuale atteso, alla data di
calcolo della riserva, degli impegni futuri dell’assicuratore e il valore attuale
atteso degli impegni dell’assicurato.
• Il principio di equità richiede che al momento della stipulazione del contratto
l’impegno del contraente e dell’assicuratore coincidano:
E
0
(I
(c )
x
) = E
0
(I
(a )
x
)
• Tale uguaglianza non sussiste necessariamente in epoche di valutazione diverse
dal momento della stipulazione de contratto:
E t ( I x( c ) ) ≠ E t ( I x( a ) )
• Tale relazione può essere trasformata in uguaglianza introducendo la riserva
matematica:
E t ( I x( a ) ) = E t ( I x( c ) ) + V t ( p )
• Da cui si può ricavare la formulazione della riserva matematica prospettiva:
V t ( p ) = E t ( I x( a ) ) − E t ( I x( c ) )
Alcuni commenti
• Accanto alla riserva matematica possono risultare necessari ulteriori
accantonamenti per far fronte a particolari impegni che gravano sul
contratto. In particolare possono essere previste, ad esempio, delle riserve
spese di gestione per far fronte alle spese che si originano nei contratti.
• Inoltre, l’utilizzo di basi tecniche di primo ordine per il calcolo della riserva
matematica potrebbe portare ad una sottostima dell’impegno rispetto
all’effettiva realtà demografica e finanziaria.
• Alcune circolari Isvap hanno, così, previsto la necessità di effettuare
accantonamenti nel caso di variazioni sfavorevoli di alcune ipotesi:
- la circolare 343 D prevede l’accantonamento di una riserva basi
demografiche per i contratti di rendita o con opzione per tener conto del
longevity risk
- la circolare 1801 prevede la stima della capacità delle riserve attuali di far
fronte agli impegni futuri legati ai contratti rivalutabili sulla base dei
rendimenti previdibili attesi.
Il ruolo dell’attuario
e l’impatto del progetto Solvency II
Il ruolo dell’attuario incaricato
¾ Principali compiti dell’attuario incaricato nel settore danni:
- una verifica preventiva delle basi tecniche, delle metodologie
statistiche, delle ipotesi tecniche e finanziarie utilizzate ai fini della
determinazione del fabbisogno tariffario e degli ulteriori elementi
considerati;
- una valutazione preventiva dei premi di tariffa in funzione dei
parametri di riferimento utilizzati;
- la stesura di una relazione tecnica sulla tariffe e sulle riserve;
- lo stabilire rapporti diretti con l’Isvap, con la società di
revisione e con il collegio sindacale.
I Principi Contabili Internazionali (IAS)
e la riserva sinistri (1/2)
¾ I principi IAS sono stati stabiliti al fine di creare una
contabilità internazionale uniforme
per ciascuna attività economica
• In un’ottica di “globalizzazione” il risultato delle
imprese deve essere confrontabile a livello internazionale
A differenza di quanto stabilito dal Codice Civile
nazionale, il cui principio cardine è quello della prudenza,
i nuovi Principi Contabili Internazionali (IAS) tendono a
privilegiare il principio della competenza.
I Principi Contabili Internazionali (IAS)
e la riserva sinistri (2/2)
¾ Principio della competenza
I bilanci devono presentarsi senza alcuna asimmetria:
- dovranno essere contabilizzati anche proventi non realizzati
sotto la voce costi e ricavi;
- verrà favorito il criterio del valore corrente ( “fair value”),
anziché quello del “costo storico” per quanto riguarda le voci
attività e passività.
Sono richiesti metodi di valutazione capaci di assicurare
una maggiore armonizzazione delle pratiche nazionali
La necessità di modelli stocastici
¾ Sia nell’ottica di introduzione dei nuovi principi contabili
internazionali, sia nell’ottica dell’individuazione di un requisito di
solvibilità secondo i principi di Solvency II, appare necessaria una
valutazione “Market Consistent” delle riserve tecniche.
¾ Tale valutazione, definita anche al “fair value”, prevede la
quantificazione non solo del valore puntuale della riserva tecnica ma
una descrizione della variabilità della stessa ed eventualmente
dell’intera distribuzione di probabilità della riserva
¾ In quest’ottica assumono particolare rilevanza metodi che
permettono la determinazione non solo del valore puntuale ma
anche una stima della variabilità (metodi stocastici)
Una valutazione “market consistent”
L’impatto del progetto Solvency II
¾ Una rilevante fonte di rischio per le compagnie di assicurazione contro i
danni è costituita dalla possibile sottostima degli impegni di rimborso in
essere, da cui la conseguente insufficienza della riserva sinistri
• In tale ambito uno degli argomenti più dibattuti negli ultimi anni riguarda
l’impiego di metodologie di calcolo di tipo deterministico o stocastico per la
valutazione della riserva sinistri
• A seguito del progetto Solvency II, l’impiego di metodologie stocastiche
dovrà diffondersi sempre di più…………
- Tra i vari aspetti il CEIOPS (Committee of European Insurance and
Occupational Pension Supervisors), su richiesta della Commissione Europea,
ha posto come obiettivo il raggiungimento di un benchmark armonizzato in
chiave probabilistica quale requisito regolamentare per la riserva sinistri
¾ Questo obiettivo può essere raggiunto solamente mediante l’utilizzo di un
modello di valutazione di tipo stocastico alla serie storica dei sinistri
I nuovi requisiti di riserva
¾ Il nuovo sistema di calcolo delle riserve dovrebbe basarsi sulla somma
di due distinte componenti:
- la best estimate, quale valore medio atteso dei futuri impegni nei confronti
degli assicurati;
- il risk margin, quale margine addizionale predisposto per formalizzare
quantitativamente l’incertezza degli impegni futuri, generata da fattori di rischio esogeni
• Mentre la definizione della best estimate come valore atteso della distribuzione dei
futuri impegni nei confronti degli assicurati è condivisa da molti, vi è in corso un
ampio dibattito per quel che riguarda la definizione quantitativa del risk margin
• È prassi comune che il risk margin debba rappresentare un margine prudenziale
destinato a compensare l’incertezza attinente gli importi futuri delle prestazioni
secondo una impostazione coerente con una valutazione di mercato
In questa ottica il risk margin rappresenterebbe il premio per il rischio
che un altro assicuratore richiederebbe per rilevare gli impegni in essere
del portafoglio considerato in una libera trattativa di mercato
Il risk margin (1/2)
¾ Nell’ambito del progetto Solvency II sono stati presi in esame due
metodi per il calcolo del risk margin:
- il quantile approach, secondo il quale il risk margin è definito come
la differenza tra il valore degli obblighi futuri scelto ad un prefissato
livello di probabilità, tipicamente uguale al 75-esimo o 90-esimo
quantile, e la best estimate;
- il cost-of-capital approach, secondo il quale il risk margin è dato dal costo
del patrimonio di vigilanza (reserve risk capital) richiesto dalla normativa per
coprire il rischio di insolvenza fino all’estinzione completa della riserva sinistri.
Il risk margin (2/2)
- il quantile approach, secondo il quale
il risk margin è definito come la
differenza tra il valore degli obblighi
futuri scelto ad un prefissato livello di
probabilità, tipicamente uguale al 75esimo quantile, e la best estimate;
- il cost-of-capital approach, secondo il
quale il risk margin è dato dal costo del
patrimonio di vigilanza (reserve risk
capital) richiesto dalla normativa per
coprire il rischio di insolvenza fino
all’estinzione completa della riserva
sinistri.
CoC_factor = 6%
(SCR): è il livello di capitale che un assicuratore dovrebbe disporre,
in un approccio di tipo going-concern, prefissato un certo livello
di confidenza ed un certo orizzonte temporale
Il prediction error (1/2)
¾ Un aspetto di interesse nella pratica attuariale è quello di
ottenere l’errore di previsione della riserva totale
Data la correlazione nella procedura di stima, presente sia
tra le righe (anni di generazione) che tra le colonne
(anni di bilancio),
la varianza di previsione non può essere determinata sommando
semplicemente le varianze di previsione delle riserve delle
singole generazioni
anche se i pagamenti cumulati corrispondenti a differenti
generazioni sono indipendenti per ipotesi
Il prediction error (2/2)
¾ La variabilità totale del processo deve includere sia la variabilità
insita nei dati stimati (varianza del processo), sia l’incertezza nella
stima dei parametri (varianza della stima)
• Sotto la tipica assunzione di indipendenza tra le osservazioni
passate e quelle future ed ipotizzando la correttezza…….
Scomposizione dell’errore quadratico medio di previsione
(RMSEP, dall’inglese Root Mean Squared Error of Prediction)
(
)
2
RMSEP = E ⎡ X − X̂ ⎤ =
⎢⎣
⎥⎦
[
= E ( X − E ( X ))
2
]
varianza di previsione
varianza del processo
rappresenta la variabilità
presente nei dati iniziali
+
(
( )) ⎤⎥⎦
E ⎡ Xˆ − E Xˆ
⎢⎣
2
varianza della stima
(la cui radice quadrata è lo
standard error)
PREDICTION ERROR =
rappresenta la variabilità
dovuta alla stima
RMSEP
La riassicurazione
La riassicurazione
¾ L’attività concernente le assicurazioni contro i danni è
tipicamente basata sulla gestione di un portafoglio di
rischi sufficientemente omogenei, in base allo stato di
informazione disponibile all’epoca di stipulazione dei contratti
aspetti che non emergono nel caso l’interesse
sia focalizzato sul singolo rapporto
assicurativo
Quantificazione della
rischiosità del portafoglio
Limitazione della
rischiosità del portafoglio
Quantificazione della rischiosità
del portafoglio
¾ Avviene mediante opportuni valori sintetici del portafoglio
1) l’indice di fluttuazione
2) l’indice di rischio
3) l’indice di stabilità relativa
9 Indici sintetici che consentono di avere una visione
globale dell’attività assicurativa
- l’ambito di riferimento è l’intero portafoglio
assicurativo, non il singolo contratto
Limitazione della rischiosità
del portafoglio
¾ Avviene mediante opportuni strumenti
1) la coassicurazione
mediante la quale l’assicuratore assume ciascun rischio in
compartecipazione con altri assicuratori, detti coassicuratori,
e ciascuno di essi diviene responsabile, in caso di sinistro,
per la frazione di rischio assunta
2) la riassicurazione
mediante la quale l’assicuratore trasferisce ad un altro
soggetto, detto riassicuratore, (almeno) una parte
(di alcuni) dei rischi assunti
Valutazione della rischiosità di un portafoglio
di assicurazioni contro i danni (1/2)
¾ Si consideri un portafoglio costituito da n contratti di
assicurazione contro i danni riferiti a un medesimo tipo di rischio
Tali contratti siano:
- contemporaneamente stipulati
- contraddistinti da un eguale periodo di copertura (annuale)
- relativi a rischi analoghi con riferimento
a. alle caratteristiche del rischio adeguatamente
valutabili, all’epoca di stipulazione del contratto,
da parte dell’assicuratore;
b. alle condizioni contrattuali di copertura, ma non
necessariamente anche ai valori monetari di
esposizione al rischio
Valutazione della rischiosità di un portafoglio
di assicurazioni contro i danni (2/2)
¾ In relazione al j-esimo (j=1,2,…,n) contratto si ha
numero di sinistri che
colpiscono il contratto
risarcimento a carico dell’assicuratore in relazione
all’i-esimo sinistro in ordine cronologico (i=0,1,…;Y0,j≡0)
Nj
X j = ∑ Yi , j
i =0
n
n
X = ∑ Xj = ∑
j=1
risarcimento globale posto a carico
dell’assicuratore per il singolo contratto
del portafoglio
Nj
∑
j=1 i = 0
Yi, j
risarcimento globale a carico
dell’assicuratore
(considerando l’intero portafoglio)
Guadagno di portafoglio (1/2)
¾
Gj = Π j − X j
Guadagno relativo al j-esimo
contratto del dato portafoglio
premio puro relativo al j-esimo
contratto del dato portafoglio
¾ Principali valori caratteristici della distribuzione di probabilità di Gj
• E ( G j ) = Π j − Pj = r j
2
var(
G
)
=
var(
X
)
=
σ
•
j
j
j
dove Pj e rj indicano,
rispettivamente, il premio equo
(vale a dire, Pj=E(Xj))
ed il caricamento di sicurezza
per il dato contratto
Guadagno di portafoglio (2/2)
¾ G=
n
∑G
j =1
j
Guadagno
di portafoglio
=Π−X
n
n
j =1
j =1
Π = ∑ Π j = ∑ ( Pj + rj ) = P + r
n
E (G ) = ∑ rj = r
j =1
n
var(G ) = var( X ) = ∑ σ 2j = σ 2
j =1
nell’ipotesi che i
risarcimenti globali
X1, X2, …, Xn siano tra
loro indipendenti
Probabilità annuale di perdita (1/3)
¾ Probabilità dell’evento
“l’onere aleatorio per risarcimenti supera l’ammontare
globale dei premi puri”
Pr{G < 0} = Pr{X > P + r} = η
probabilità annuale di perdita
probabilità per l’assicuratore di non riuscire a
fronteggiare l’onere di sinistrosità impiegando le sole
risorse provenienti dai premi
9 L’obiettivo è quello di mantenere sufficientemente bassa, in particolare
eguale ad una data soglia η* ritenuta accettabile, tale probabilità
Probabilità annuale di perdita (2/3)
¾ Si può convenientemente considerare la variabile
aleatoria standardizzata
X −P
σ
σ = σ(X)
scarto quadratico
medio di X
⎧X −P r ⎫
⎛r⎞
> ⎬ = 1 − Φ⎜ ⎟
η = Pr ⎨
σ⎭
⎩ σ
⎝σ ⎠
Φ : funzione
di ripartizione
di (X-P)/σ
Obiettivo dell’assicuratore è “controllare” la probabilità η
mediante il caricamento di sicurezza (globale) r
Probabilità annuale di perdita (3/3)
¾ Non formulando alcuna ipotesi sulla distribuzione
di probabilità di X
⎧X −P r ⎫
⎛r⎞
> ⎬ = 1 − Φ⎜ ⎟
η = Pr ⎨
σ⎭
⎩ σ
⎝σ ⎠
r
σ
= Φ −1 (1 − η )
dove Φ-1(1-η) è il percentile di
ordine (1-η) della distribuzione
di probabilità di (X-P)/σ
Fissato un livello, η* (ad esempio η* = 0.005), che l’assicuratore
ritiene accettabile per la probabilità annuale di perdita si ricava il
valore (r/σ)* di r/σ che consente di raggiungere il dato obiettivo
Probabilità annuale di perdita
OSSERVAZIONI
1) Nella particolare ipotesi che il portafoglio sia costituito da
un numero sufficientemente grande di contratti, si può
opportunamente assumere l’approssimazione normale per
la distribuzione di probabilità di X (con valore medio P e
scarto quadratico medio σ).
- In tal caso Φ è la funzione di ripartizione della
distribuzione normale standardizzata
2) Posto
μ=
r
σ
μ = Φ −1 (1 − η )
è immediato rilevare come il caricamento di sicurezza, r, da
applicare (globalmente) al portafoglio sia proporzionale allo
scarto quadratico medio, σ, del risarcimento globale X
Indice di fluttuazione e indice di rischio
¾ Indice di fluttuazione
σ
r
ξ = =μ
P
P
Aliquota di caricamento di sicurezza (per unità di
premio equo) da applicare in corrispondenza di
ciascun contratto del portafoglio
¾ Indice di rischio
ρ=
σ
P
coefficiente di variazione di X
A differenza dell’indice di fluttuazione, ξ, il quale dipende dal
fissato livello di caricamento di sicurezza μ, il rapporto ρ
costituisce una misura oggettiva di rischio del portafoglio
Probabilità annuale di rovina (1/2)
¾ Probabilità dell’evento
“l’onere aleatorio per risarcimenti supera la somma
dell’ammontare globale dei premi puri e del margine di
solvibilità inizialmente a disposizione dell’assicuratore
in relazione al portafoglio”
ε = Pr{G < -W} = Pr{X > W + P + r}
Probabilità annuale di rovina
probabilità per l’assicuratore di non riuscire a fronteggiare
l’onere di sinistrosità pur impiegando tutte le risorse,
costituite dai premi e dai mezzi propri, a sua disposizione
Probabilità annuale di rovina (2/2)
ε = Pr{G < -W} = Pr{X > W + P + r}
W : margine di solvibilità, costituito da mezzi propri
(capitale, riserve libere) dell’assicuratore non destinati,
a differenza delle riserve tecniche, alla copertura di
specifici impegni in termini di valore atteso
¾ Altro obiettivo dell’assicuratore consiste nel mantenere
sufficientemente bassa, in particolare eguale ad una data soglia
ε* ritenuta accettabile, tale probabilità
⎧X −P W +r⎫
⎛W + r ⎞
ε = Pr ⎨
>
⎟
⎬ = 1 − Φ⎜
σ ⎭
⎩ σ
⎝ σ ⎠
Indice di stabilità relativa di portafoglio
¾
s=
W +r
σ
Fissato un livello, ε* (ad esempio ε* = 0.001), che
l’assicuratore ritiene accettabile per la probabilità
annuale di rovina
Dalla s = Φ-1(1-ε*)
⎧X −P W +r⎫
⎛W + r ⎞
1
>
=
−
Φ
⎟
⎜
⎬
σ ⎭
⎩ σ
⎝ σ ⎠
dove ε = Pr ⎨
si ottiene il valore s* dell’indice di stabilità relativa, s, che
consente di raggiungere il dato obiettivo
Indice di stabilità relativa di portafoglio
OSSERVAZIONI (1/2)
1) Dalla s = Φ-1(1-ε*) è immediato rilevare come la
probabilità annuale di rovina, ε, decresca al crescere
dell’indice di stabilità relativa, s, del portafoglio
2) Nella particolare ipotesi che il portafoglio sia costituito da
un numero sufficientemente grande di contratti, si può
opportunamente considerare l’approssimazione normale
ai fini della distribuzione di probabilità di X
3) L’indice di stabilità relativa del portafoglio ha interesse
anche quando, non formulando alcuna ipotesi sulla
distribuzione di probabilità di (X-P)/σ, si scelga di ricorrere
al calcolo di limitazioni superiori per la probabilità di rovina
Indice di stabilità relativa di portafoglio
OSSERVAZIONI (2/2)
¾ Probabilità di rovina e indice di stabilità
relativa di portafoglio
Dalla disuguaglianza di Cantelli
1
Pr{X - P ≥ tσ } ≤
1+ t 2
con t > 0
Posto tσ = W+r (quindi, t = s), si ottiene
1
Pr{G ≤ - W} ≤
1+ s2
L’indice di stabilità relativa di portafoglio pone una
limitazione superiore alla probabilità di rovina
Probabilità annuale di rovina e
indice di stabilità relativa di portafoglio (1/2)
¾ Al fine di ridurre la probabilità annuale di rovina, ε,
l’assicuratore può opportunamente operare sull’indice di
stabilità relativa del portafoglio, s
incrementando almeno una delle seguenti due
variabili decisionali
a) il margine di solvibilità, W
- frequentemente ostacolata dall’effettiva situazione
patrimoniale dell’assicuratore
b) il caricamento di sicurezza, r
- spesso resa problematica dalle condizioni di
mercato
Probabilità annuale di rovina e
indice di stabilità relativa di portafoglio (2/2)
¾ Nelle situazioni in cui è fortemente limitata la possibilità
di intervento sulle precedenti variabili decisionali
l’assicuratore deve ricorrere a strumenti che accrescano
l’indice di stabilità relativa del portafoglio mediante una
riduzione dello scarto quadratico medio, σ, del
risarcimento globale X
la coassicurazione
la riassicurazione
Coassicurazione e riassicurazione (1/2)
¾ Coassicurazione
l’assicuratore assume ciascun rischio in compartecipazione
con altri assicuratori, detti coassicuratori,
e ciascuno di essi diviene responsabile, in caso di sinistro,
per la frazione di rischio assunta
¾ Riassicurazione
l’assicuratore trasferisce ad un altro soggetto, detto
riassicuratore, (almeno) una parte (di alcuni)
dei rischi assunti
Coassicurazione e riassicurazione (2/2)
¾ Coassicurazione
Si attua un trasferimento del rischio su
base orizzontale (vale a dire, riferito all’epoca di
stipulazione del contratto di assicurazione)
e l’assicurato è a conoscenza dell’esistenza
del rapporto coassicurativo
¾ Riassicurazione
Si attua un trasferimento del rischio su
base verticale (vale a dire, successivo all’epoca di
stipulazione del contratto di assicurazione)
e l’assicurato è del tutto estraneo
al rapporto riassicurativo
Rapporti e trattati di riassicurazione (1/6)
¾ In generale, un rapporto di riassicurazione si instaura
secondo una delle seguenti due modalità
a) tra l’assicuratore, detto cedente, ed un altro
assicuratore, il quale opera come riassicuratore
cessionario
b) tra l’assicuratore cedente ed un riassicuratore
professionale, il quale non svolge lavoro diretto
(vale a dire, non offre copertura ai rischi provenienti
direttamente dagli assicurati)
Rapporti e trattati di riassicurazione (2/6)
¾ Riassicurazione passiva e riassicurazione attiva
a) La cessione dei rischi operata dall’assicuratore
(cedente) è denominata riassicurazione passiva
b) L’assunzione dei rischi operata dal riassicuratore
(sia egli cessionario o professionale) viene denominata
riassicurazione attiva (o, anche, lavoro indiretto in
quanto questa attività non deriva dalle acquisizioni
dirette dei rischi degli assicurati)
• E’ frequente il caso in cui il riassicuratore non accetti
l’intera cessione dei rischi richiesta dall’assicuratore
- quest’ultimo ricorrerà ad un secondo riassicuratore
(eventualmente ad un terzo, …) al quale cederà le parti
residue di rischio non accettate dal primo riassicuratore
Rapporti e trattati di riassicurazione (3/6)
¾ Riassicurazione di secondo livello
Caso in cui il riassicuratore, dopo avere accolto la
richiesta dell’assicuratore, procede alla cessione ad
altro riassicuratore (di una parte) dei rischi accettati
La riassicurazione di secondo livello è denominata
retrocessione e i soggetti in essa coinvolti sono
chiamati, rispettivamente, retrocedente e
retrocessionario
9 È il riassicuratore ad attuare un nuovo rapporto di
riassicurazione; e non l’assicuratore diretto
Rapporti e trattati di riassicurazione (4/6)
¾ Il rapporto tra l’assicuratore ed il riassicuratore può inoltre
avvenire secondo una delle seguenti tre modalità
a) riassicurazione facoltativa;
- la cessione è effettuata contratto per contratto, secondo
le specifiche esigenze dell’assicuratore
- il riassicuratore può non accettare la cessione
b) riassicurazione obbligatoria e riassicurazione “facob”
(vale a dire, facoltativa-obbligatoria)
- il rapporto tra le parti è regolamentato da
un trattato di riassicurazione che ne disciplina i diversi
aspetti
(date di inizio e fine rapporto, la forma riassicurativa, i limiti di
ritenzione dell’assicuratore, i limiti di accettazione del riassicuratore,
l’importo e le modalità di pagamento del premio di riassicurazione)
Rapporti e trattati di riassicurazione (5/6)
b) riassicurazione obbligatoria
l’assicuratore è obbligato a cedere assegnate quote di
rischio ed il riassicuratore è obbligato ad accettarle
(il trattato è pertanto anche detto automatico)
c) riassicurazione “facob”
il riassicuratore è obbligato ad accettare, entro
limiti prestabiliti, le quote di rischio che
l’assicuratore decide di cedere
OSSERVAZIONE
1) Le forme riassicurative facoltative riguardano
prevalentemente singoli rischi.
- Ad esse si rivolge di norma l’assicuratore per coprire nuovi rischi,
difficilmente inseribili all’interno di un collettivo preesistente e
caratterizzato dal requisito dell’omogeneità
2) I trattati di riassicurazione riguardano, per lo più, gruppi di rischi
Rapporti e trattati di riassicurazione (6/6)
¾ Riassicurazione individuale e
riassicurazione globale
Il rapporto di riassicurazione, qualunque sia la modalità
prescelta, può infine essere definito in base ad un approccio
a) individuale (vale a dire, con riferimento al
singolo contratto): in questo caso si ha una
riassicurazione individuale
b) globale (vale a dire, con riferimento
all’intero portafoglio): in questo caso si
ha una riassicurazione globale
Forme di riassicurazione (1/2)
¾ Si distinguono le seguenti due forme di riassicurazione
a) riassicurazione proporzionale;
l’assicuratore e il riassicuratore si accordano su una
ripartizione di ciascun rischio del portafoglio.
- Nella medesima proporzione viene ripartito il
risarcimento relativo a ciascun eventuale sinistro
b) riassicurazione non proporzionale;
l’assicuratore e il riassicuratore si accordano
generalmente su un importo monetario
corrispondente al massimo risarcimento che
l’assicuratore è disposto ad effettuare, secondo la
particolare modalità riassicurativa prescelta
Forme di riassicurazione (2/2)
b) riassicurazione non proporzionale;
L’importo monetario corrispondente al massimo
risarcimento che l’assicuratore è disposto ad
effettuare viene valutato in riferimento a:
- ad un sinistro che colpisce un dato contratto del
portafoglio;
- ai sinistri che, derivanti da un unico evento (il quale può
avere, in particolare, natura catastrofale), colpiscono
contemporaneamente più contratti del portafoglio;
- ai sinistri che, nel corso di un assegnato intervallo di
tempo (ad esempio, un anno), colpiscono il portafoglio
9 Con riferimento a quest’ultima modalità l’accordo tra le parti può, in alternativa, essere
basato sul rapporto percentuale sinistri a premi di competenza (“loss ratio”) del
portafoglio, considerando quindi una limitazione espressa in termini percentuali (e non in
termini monetari) ai fini della ripartizione del risarcimento globale tra le parti
Forme di riassicurazione
OSSERVAZIONI
1) La riassicurazione operante tra due assicuratori può
prevedere una clausola di reciprocità, in base alla quale
i due assicuratori concordano la reciproca cessione, in
un’assegnata misura, dei rischi direttamente acquisiti sul
mercato
2) Nella pratica riassicurativa le forme proporzionali e
non proporzionali sono frequentemente combinate tra
loro, definendo in questo modo varie riassicurazioni
miste particolarmente efficaci per le diverse esigenze
dell’assicuratore e del riassicuratore
La riassicurazione: obiettivi e ruoli (1/2)
¾ L’obiettivo principale della riassicurazione,
considerando il punto di vista dell’assicuratore,
è evidentemente la riduzione della
rischiosità del portafoglio
- In conseguenza si determina anche un aumento
della capacità di assunzione dei rischi
- La considerazione che la riassicurazione può
determinare un significativo rafforzamento della
solvibilità dell’assicuratore
ad esempio misurata mediante il rapporto tra l’ammontare
dei mezzi propri ed il volume dei premi incassati, calcolati
al netto delle cessioni in riassicurazione
La riassicurazione: obiettivi e ruoli (2/2)
¾ Il rapporto riassicurativo fa anche sì che l’assicuratore
possa ricevere, nella fase di progettazione di nuovi prodotti
assicurativi, un’adeguata assistenza tecnica
(innanzitutto, nella scelta delle basi tecniche)
da parte del riassicuratore.
- In special modo se il rapporto viene instaurato con un
riassicuratore professionale
• OBIETTIVO DEL RIASSICURATORE
Dal punto di vista del riassicuratore va invece
segnalato l’obiettivo di quest’ultimo di poter partecipare
alla totalità (o, quanto meno, alla gran parte) degli
impegni assunti dall’assicuratore
La riassicurazione: profili attuariali (1/2)
¾ Si consideri un portafoglio costituito da n contratti di
assicurazione contro i danni contemporaneamente stipulati,
aventi un eguale periodo (annuale) di copertura
e relativi a rischi analoghi
- La riassicurazione del portafoglio può essere
opportunamente descritta tramite una n-pla di applicazioni
Xj ⎯
⎯→ X jA ,
j = 1,2,..., n
che decrivono, nei riguardi dei singoli contratti del portafoglio,
il risarcimento globale conservato dall’assicuratore,
indicato con X Aj
La riassicurazione: profili attuariali (2/2)
¾ Il risarcimento globale ceduto al riassicuratore
è pertanto dato dalla
X Rj = X j − X jA
ed è indicato con X Rj
Con riferimento all’intero portafoglio si ha il
risarcimento globale conservato dall’assicuratore
n
X = ∑ X jA
A
j =1
ed il risarcimento globale ceduto al riassicuratore
n
X = ∑ X Rj = X − X A
R
j =1
Riassicurazioni proporzionali
¾ Nell’ambito della riassicurazione proporzionale si
hanno le seguenti forme riassicurative
1) riassicurazione in quota;
2) riassicurazione per eccedente di somma
Entrambe le garanzie prevedono che il rapporto tra
l’assicuratore ed il riassicuratore sia definito a livello
di singolo contratto (riassicurazione individuale)
Riassicurazione in quota
¾ Nella riassicurazione in quota (o, anche, riassicurazione
“quota-share”) l’assicuratore ed il riassicuratore fissano un’unica
aliquota di conservazione (o, anche, aliquota di ritenzione)
che è applicata all’esposizione monetaria associata a
ciascun contratto del portafoglio.
- Tale esposizione monetaria è espressa in termini di
a) valore (del bene) assicurato o valore del
massimo danno probabile, nel caso di
assicurazioni di danni a beni di proprietà;
b) massimale di garanzia, nel caso di
assicurazioni di responsabilità civile
Riassicurazione in quota
ESEMPIO (1/2)
In un portafoglio di assicurazioni di danni a beni di proprietà costituito
da n contratti, contemporaneamente stipulati, di durata annuale e con
valori assicurati V1, V2, …, Vn, sia a (0<a<1) l’aliquota di
conservazione concordata tra le parti e, quindi, (1-a) l’aliquota
corrispondente alla cessione in riassicurazione
• In relazione al j-esimo contratto del portafoglio il valore assicurato
conservato dall’assicuratore è quindi
V jA = aV j
mentre il valore assicurato ceduto al riassicuratore è
V jR = (1 − a )V j
Riassicurazione in quota
ESEMPIO (2/2)
• In relazione all’intero portafoglio il risarcimento globale conservato
dall’assicuratore è
n
n
X A = ∑ X jA = a ∑
j =1
Nj
∑Y
i, j
j =1 i = 0
mentre il risarcimento globale ceduto al riassicuratore è
n
n
X R = ∑ X Rj = (1 − a ) ∑
j =1
Nj
∑Y
j =1 i = 0
i, j
Riassicurazione in quota
OSSERVAZIONI
1) È molto semplice a fini operativi
2) Riesce ad aumentare significativamente la capacità di
assunzione dei rischi da parte dell’assicuratore
3) Malgrado riduca la variabilità (in termini assoluti) del
risarcimento globale a carico dell’assicuratore, non
realizza un’efficace omogeneizzazione dei valori assicurati
e, quindi, non si ottiene una soddisfacente riduzione della
rischiosità del portafoglio
4) Dal punto di vista del riassicuratore va evidenziato
l’aspetto positivo derivante dalla sua partecipazione
alla totalità degli impegni assunti dall’assicuratore
Riassicurazione per eccedente di somma
¾ Nella riassicurazione per eccedente di somma
(o, anche, riassicurazione “surplus”) l’assicuratore
ed il riassicuratore fissano un pieno di conservazione
corrispondente alla massima esposizione al rischio,
in termini monetari, che l’assicuratore accetta di
conservare per ciascun contratto.
ESEMPIO
In un portafoglio di assicurazioni di danni a beni di proprietà
costituito da n contratti, contemporaneamente stipulati,
di durata annuale e con valori assicurati V1, V2, …, Vn,
sia C il pieno di conservazione concordato tra le parti
Riassicurazione per eccedente di somma
ESEMPIO (1/3)
• Il valore assicurato conservato dall’assicuratore è
V jA = min (V j ; C )
mentre il valore assicurato ceduto al riassicuratore, detto
eccedente (o, anche, “surplus”), è
V jR = max (V j − C ; 0 )
Riassicurazione per eccedente di somma
ESEMPIO (2/3)
• In relazione al j-esimo contratto del portafoglio la
riassicurazione per eccedente di somma individua l’aliquota
di conservazione
aj =
min (V j ; C )
Vj
⎛C ⎞
= min⎜ ;1⎟
⎜V ⎟
⎝ j ⎠
con 0 ≤ aj ≤ 1
Nella riassicurazione per eccedente di somma i limiti di
accettazione stabiliti dal riassicuratore, come il seguente
esempio pone in evidenza, sono di norma espressi in
multipli interi del pieno di conservazione
Riassicurazione per eccedente di somma
ESEMPIO (3/3)
• In relazione all’intero portafoglio il risarcimento globale
conservato dall’assicuratore è
n
∑
XA=
j =1
X iA =
n
Nj
∑∑a
j =1 i = 0
j
Yi , j
mentre il risarcimento globale ceduto al riassicuratore è
XR =
n
∑
j =1
X iR =
n
Nj
∑ ∑ (1 − a ) Y
j =1 i = 0
j
i, j
Riassicurazione per eccedente di somma
OSSERVAZIONI (1/2)
1) La riassicurazione per eccedente di somma, è contraddistinta
da una maggiore complessità operativa rispetto alla
riassicurazione in quota
2) Realizza un’efficace omogeneizzazione dei valori assicurati
e, quindi, una significativa riduzione della rischiosità del
portafoglio
- a parità di sacrificio per l’assicuratore in termini di valore atteso del
guadagno di portafoglio (vale a dire, in termini di caricamento di sicurezza),
comporta una maggiore riduzione della probabilità di rovina rispetto al
caso della riassicurazione in quota
- sotto opportune ipotesi, la riassicurazione per eccedente di somma
rappresenta la garanzia riassicurativa che ottiene la minima probabilità
di rovina per ogni assegnato livello di sacrificio fissato dall’assicuratore
Riassicurazione per eccedente di somma
OSSERVAZIONI (2/2)
3) Per quanto concerne la provvigione di riassicurazione
riconosciuta all’assicuratore si osserva che in questo caso essa
è di norma inferiore a quella prevista nella riassicurazione in
quota
la cessione riguarda i rischi più grandi (generalmente, i
peggiori) e gli utili attesi trasferiti al riassicuratore sono
pertanto sensibilmente ridotti
9 Al riassicuratore viene trasferita la parte più elevata
dell’ammontare dei risarcimenti relativa ad ogni esborso
Combinazioni di riassicurazioni
proporzionali (1/2)
¾ Nei mercati riassicurativi sono talvolta applicate
combinazioni di coperture riassicurative proporzionali
• In riferimento ad un portafoglio di assicurazioni di danni a beni di
proprietà costituito da n contratti contemporaneamente stipulati, di durata
annuale e con valori assicurati V1, V2, …, Vn
ESEMPIO 1
assicuratore che conserva la quota a (0<a<1) di ciascun contratto
del portafoglio, con una massima esposizione monetaria eguale al
pieno di conservazione C
a 'j
=
(
min aVj ; C
Vj
) = min⎛⎜ C ; a ⎞⎟
⎜ Vj
⎝
⎟
⎠
In riferimento al j-esimo
contratto del portafoglio
Combinazioni di riassicurazioni
proporzionali (2/2)
ESEMPIO 2
assicuratore che conserva la quota a (0<a<1) di ciascun contratto
del portafoglio per il quale ha in precedenza operato una
cessione riassicurativa per eccedente di somma con
pieno di conservazione C
• Aliquota di conservazione in riferimento al j-esimo contratto
del portafoglio
a =
''
j
a min (V j ; C )
Vj
⎛ aC ⎞
= min⎜
;a⎟
⎜V
⎟
⎝ j ⎠
Riassicurazioni non proporzionali
¾ Nell’ambito della riassicurazione non proporzionale si
hanno le seguenti forme riassicurative
1) riassicurazione “excess of loss”;
2) riassicurazione “stop-loss”.
Il rapporto tra l’assicuratore ed il riassicuratore può
essere definito a livello di singolo contratto
(riassicurazione individuale)
oppure a livello di portafoglio
(riassicurazione globale)
Riassicurazione “excess of loss”
¾ Nella riassicurazione “excess of loss” l’assicuratore e
il riassicuratore fissano un importo monetario, denominato
priorità, corrispondente al massimo risarcimento che
l’assicuratore è disponibile ad effettuare, secondo la
particolare modalità riassicurativa prescelta
• La priorità è fissata in relazione:
a) ad un sinistro che colpisce un dato contratto del
portafoglio, riassicurazione “per risk excess of loss”
b) ai sinistri che, derivanti da un unico evento, colpiscono
più contratti del portafoglio contemporaneamente,
riassicurazione “per event excess of loss”
c) ai sinistri che, nel corso di un assegnato intervallo di
tempo (ad esempio, un anno), colpiscono il portafoglio,
riassicurazione “aggregate excess of loss”
Riassicurazione “per risk excess of loss” (1/3)
Con riferimento ad un portafoglio di assicurazioni di responsabilità
civile costituito da n contratti contemporaneamente stipulati, di durata
annuale e con massimali di garanzia M1,M2,…,Mn
¾ Sia Lj la priorità fissata in corrispondenza
del j-esimo contratto
Y = min (Yi , j ; L j )
A
i, j
Importo che rimane a carico
dell’assicuratore in relazione all’i-esimo
sinistro che colpisce il contratto
• Se il trattato non prevede limiti di accettazione da parte
del riassicuratore
Yi ,Rj = max (Yi , j − L j ; 0 )
Importo che viene trasferito al
riassicuratore in relazione all’i-esimo
sinistro che colpisce il contratto
È trasferita l’intera eccedenza rispetto alla priorità
Riassicurazione “per risk excess of loss” (2/3)
¾ La massima esposizione del riassicuratore nei confronti
di un sinistro è definita portata
• La portata può essere:
- totale (vale a dire, eguale alla differenza Mj-Lj)
- parziale (vale a dire, inferiore alla differenza Mj-Lj)
• Risarcimento globale conservato dall’assicuratore in relazione
all’intero portafoglio
n
XA =∑
Nj
A
Y
∑ i, j =
j =1 i = 0
Nj
∑ ∑ min (Y
n
i, j
j =1 i = 0
; Lj
)
risarcimento globale ceduto al riassicuratore (portata totale)
n
X =∑
R
Nj
∑Y
j =1 i = 0
R
i, j
n
=∑
Nj
∑ max (Y
j =1 i = 0
i, j
− L j ;0
)
Riassicurazione “per risk excess of loss” (3/3)
¾ Nella pratica riassicurativa la portata prevista nella
copertura “per risk excess of loss” è generalmente parziale
• Risarcimento ceduto al riassicuratore in relazione all’i-esimo sinistro
che colpisce il j-esimo contratto del portafoglio
Portata parziale
Yi ,Rj = min[max(Yi , j − L j ;0) ; Q j ]
l’assicuratore deve pertanto procurarsi ulteriori garanzie
riassicurative, usualmente articolate in “layers” (o, anche, “fasce”)
9 Il riassicuratore che copre il primo “layer”, detto “working layer”,
è evidentemente più esposto al rischio di risarcimenti a suo carico
rispetto ai riassicuratori che coprono i “layers” successivi
Riassicurazione “per event excess of loss”
Con riferimento ad un portafoglio di assicurazioni di responsabilità civile
costituito da n contratti contemporaneamente stipulati e di durata annuale,
sia Z il risarcimento globale relativo ai sinistri che, derivanti da un
unico evento, colpiscono più contratti del portafoglio
• Sia LC la priorità fissata in corrispondenza di tale evento
Z A = min( Z ; LC )
Z = max( Z − L ;0)
R
C
Importo che rimane a carico
dell’assicuratore
Importo trasferito al
riassicuratore (portata totale)
Z R = min[max( Z − LC ;0) ; Q C ]
Importo trasferito al riassicuratore
(portata parziale, QC)
Riassicurazione “aggregate excess of loss”
Con riferimento ad un portafoglio di assicurazioni di responsabilità civile
costituito da n contratti contemporaneamente stipulati e di durata annuale,
- sia LG la priorità fissata in corrispondenza del portafoglio,
anche denominata priorità globale
X A = min( X ; LG )
X R = max( X − LG ;0)
Risarcimento globale conservato
dall’assicuratore
Importo trasferito al
riassicuratore (portata totale)
X = min[max( X − L ;0) ; Q ]
R
G
G
Importo trasferito al riassicuratore
(portata parziale, QG )
Riassicurazione “aggregate excess of loss”
OSSERVAZIONI
1) La riassicurazione “aggregate excess of loss” è molto
vantaggiosa per l’assicuratore, il quale ottiene in tal
modo la copertura dell’eventuale eccedenza positiva del
risarcimento globale nei confronti della sua previsione
2) Tale copertura non è altrettanto gradita dal riassicuratore
a causa dell’elevata aleatorietà connessa ai risarcimenti
trasferiti a suo carico
nel premio di riassicurazione vi è un più consistente caricamento di
sicurezza rispetto ad altre forme di riassicurazione
3) E’frequente l’impiego di questa copertura in
combinazione con una riassicurazione proporzionale,
in quota o per eccedente di somma
Riassicurazione “stop loss” (1/2)
¾ Nella riassicurazione “stop-loss” l’assicuratore ed il
riassicuratore stabiliscono un valore, corrispondente al
massimo risarcimento che, espresso in percentuale dei premi,
l’assicuratore è disponibile ad effettuare in relazione ai
sinistri che colpiscono il portafoglio in un anno
• Il valore concordato tra le parti è denominato
priorità globale
9 La riassicurazione “stop-loss” è definita a livello di
portafoglio (riassicurazione globale)
ed opera in modo analogo alla riassicurazione “aggregate
excess of loss”, con l’unica differenza che per la priorità globale
viene ora considerato un valore percentuale
anziché un valore monetario
Riassicurazione “stop loss” (2/2)
Con riferimento ad un portafoglio di assicurazioni di responsabilità civile
costituito da n contratti contemporaneamente stipulati e di durata annuale, si
indichi con q il rapporto aleatorio sinistri a premi di competenza del portafoglio
• Sia qSL la fissata priorità globale
Percentuale dell’ammontare
globale dei premi incassati
nell’anno conservata
dall’assicuratore
q A = min(q; q SL )
q R = max(q − q SL ;0)
R
q = min[max(q − q
SL
Percentuale ceduta
(portata totale)
;0); q*]
Percentuale ceduta
(portata parziale, q*)
Combinazioni di riassicurazioni
non proporzionali (1/2)
¾ Nei mercati riassicurativi vengono frequentemente
applicate alcune combinazioni di forme riassicurative
non proporzionali
ESEMPIO
In riferimento ad un portafoglio di assicurazioni di responsabilità civile
costituito da n contratti contemporaneamente stipulati e di durata annuale
Combinazione di una riassicurazione “per risk excess of loss”
con una riassicurazione “aggregate excess of loss”,
in linea con le seguenti ipotesi:
a) la riassicurazione “per risk excess of loss” è caratterizzata, con
riferimento al j-esimo contratto del portafoglio, da una priorità Lj
e da una portata parziale Qj
b) la riassicurazione “aggregate excess of loss” è caratterizzata da una
priorità LG e da una portata parziale QG
Combinazioni di riassicurazioni
non proporzionali (2/2)
• Risarcimento globale conservato dall’assicuratore
X = min ( X ; L )
A
A
(1)
G
n
con
X (A1) = ∑
Nj
∑ min (Y
j =1 i = 0
i, j
; Lj )
risarcimento globale conservato
dall’assicuratore per effetto della sola
componente “per risk excess of loss”
• Risarcimento globale ceduto al riassicuratore
X R = min [max ( X (R1) − LG ;0); Q G ]
con
n
X (R1) = ∑
Nj
∑ min [max (Y
j =1 i = 0
i, j
− L j ;0) ; Q j ]
risarcimento globale ceduto
al riassicuratore per effetto
della sola componente
“per risk excess of loss”
Riassicurazioni miste
ESEMPIO
Si considerino una riassicurazione “aggregate excess of loss”
ed una riassicurazione in quota
⎧
X
se X ≤ LG
⎪
XA = ⎨
⎪LG + a (X − LG ) se X > LG
⎩
⎧
0
se X ≤ LG
⎪
XR = ⎨
⎪(1 − a )(X − LG ) se X > LG
⎩
Importo che rimane a carico
dell’assicuratore
Importo trasferito al
riassicuratore
Riassicurazioni miste
OSSERVAZIONI
1) Alcune riassicurazioni miste, ottenute mediante combinazione
di una forma riassicurativa proporzionale con una forma
riassicurativa non proporzionale, sono di notevole interesse
teorico oltrechè applicativo
• SULL’ESEMPIO PROPOSTO
a) È frequentemente in uso nei mercati riassicurativi
b) È pienamente rispondente alle esigenze dell’assicuratore
c) È preferita dal riassicuratore rispetto alle due garanzie
che la compongono
- a differenza della riassicurazione “aggregate excess of loss”
coinvolge l’assicuratore anche per i sinistri eccedenti la priorità
- a differenza della riassicurazione in quota non prevede la
partecipazione del riassicuratore alla copertura dei piccoli sinistri
Il premio di riassicurazione (1/2)
¾ A fronte della cessione (parziale o totale) di rischi
l’assicuratore deve corrispondere al riassicuratore un premio
di riassicurazione, prezzo della garanzia riassicurativa
¾ In generale, esso comprende sia un caricamento di
sicurezza sia un caricamento per spese ed è inoltre
fortemente influenzato da diversi fattori di natura non tecnica:
- le condizioni del mercato riassicurativo;
- il rapporto esistente tra le parti.
• Ai fini della determinazione del premio equo di
riassicurazione occorre distinguere tra riassicurazioni
proporzionali e riassicurazioni non proporzionali
Il premio di riassicurazione (2/2)
¾ Nelle riassicurazioni proporzionali
il premio equo è ricavato applicando la percentuale di
trasferimento del rischio al corrispondente premio della
copertura assicurativa di base
¾ Nelle riassicurazioni non proporzionali
a) metodo dell’
“exposure rating”
il premio equo viene determinato
ripartendo il premio della copertura
assicurativa di base tra
l’assicuratore e il riassicuratore in
misura proporzionale
all’esposizione al rischio delle parti
b) metodo dell’
“experience rating”
il premio equo viene
determinato mediante
l’esperienza di sinistrosità,
concernente un’opportuna
collettività di rischi
riassicurati
Il premio di riassicurazione:
“EXPOSURE RATING” (1/4)
¾ L’aliquota di premio riconosciuta al riassicuratore deve
tenere conto della differenza esistente tra la distribuzione
degli importi di un sinistro e la distribuzione dei
massimali di garanzia (nel caso di assicurazioni di
responsabilità civile) oppure della distribuzione dei valori
(dei beni) assicurati (nel caso si consideri un portafoglio
di assicurazioni di danni a beni di proprietà)
Vi sarà prevalenza di sinistri di importo inferiore al
massimale
Il premio di riassicurazione:
“EXPOSURE RATING” (2/4)
ESEMPIO
Al riassicuratore che garantisce una copertura “per risk excess of
loss” con priorità eguale al 50% del massimale di garanzia di ciascun
contratto va riconosciuta un’aliquota del premio della copertura
assicurativa di base comunque inferiore al 50%………..
¾ Nella pratica riassicurativa, la ripartizione dei premi
tra le parti è di norma ottenuta utilizzando una delle
seguenti procedure:
a) si costruiscono apposite tavole, note
come “first loss scales”
b) si costruiscono apposite curve, note
come “exposure curves”
Il premio di riassicurazione:
“EXPOSURE RATING” (3/4)
¾ Procedure:
a) si costruiscono apposite tavole, “first loss scales”:
esse stabiliscono l’aliquota di premio di pertinenza del
riassicuratore per ogni valore della fissata priorità
espresso in percentuale del massimale di garanzia (o del
valore assicurato, …)
b) si costruiscono apposite curve, “exposure curves”:
apposite curve tracciate nel primo quadrante di un piano
cartesiano con
- sull’asse delle ascisse i valori percentuali del rapporto tra la
fissata priorità ed il massimale di garanzia (o il valore
assicurato, …);
- mentre sull’asse delle ordinate le corrispondenti aliquote di
premio di pertinenza dell’assicuratore
Il premio di riassicurazione:
“EXPOSURE RATING” (4/4)
• OSSERVAZIONI
a) Le “first loss scales”, costruite sulla base dei dati
raccolti nel corso del tempo da parte degli assicuratori e
dei riassicuratori, variano per categorie di rischi
assicurati e, inoltre, da un riassicuratore ad un altro
b) Le “exposure curves” si trovano sempre al di sopra della
bisettrice del primo quadrante (nel caso di coincidenza si
ha la ripartizione proporzionale dei premi in base al
rischio assunto).
- Più elevata è l’incidenza di sinistri di importo inferiore al
massimale di garanzia (o al valore assicurato, …) più
marcata è la concavità verso il basso della curva
Il premio di riassicurazione:
“EXPERIENCE RATING” (1/3)
¾ Nella pratica riassicurativa è frequentemente adottato il
metodo del “burning cost”
• Il “burning cost” è definito come il rapporto percentuale
sinistri a premi (annuali) di competenza del riassicuratore
METODO DEL “BURNIG COST”
consiste nel calcolare un’opportuna media dei valori del
“burning cost” osservati dal riassicuratore, in un dato
intervallo di tempo (per lo più, 3 o 5 anni), su un
portafoglio di rischi riassicurati
k
τ=
∑
j =1
k
∑
j =1
S Cj
Tasso di premio
PjC
Il premio di riassicurazione:
“EXPERIENCE RATING” (2/3)
• OSSERVAZIONI
1) Il tasso τ è propriamente un tasso di premio equo se i premi
presi in considerazione sono i premi equi.
- Nella pratica riassicurativa è tuttavia usuale il riferimento
ai premi di tariffa.
2) I valori del rapporto percentuale sinistri a premi di
competenza osservati in anni diversi da parte del
riassicuratore sono sottoposti ad un’opportuna indicizzazione
per poter essere confrontati tra loro
- essi sono generalmente originati da portafogli raramente
omogenei sia sotto il profilo dei rischi assicurati sia sotto il
profilo delle garanzie riassicurative adottate
Il premio di riassicurazione:
“EXPERIENCE RATING” (3/3)
¾ Il metodo del “burnig cost” può essere utilmente
utilizzato:
a) in modo retrospettivo, per adeguare nel tempo il
tasso di premio relativo ad un rischio riassicurato
b) in modo prospettivo, per ottenere la stima iniziale del
tasso di premio relativo ad un nuovo rischio riassicurato
¾ Nella pratica riassicurativa l’uso dei metodi è fortemente
condizionato:
- dai dati a disposizione del riassicuratore
- dal “layer” al quale il calcolo fa riferimento
Il premio di riassicurazione:
“EXPERIENCE RATING” E “EXPOSURE RATING”
A CONFRONTO
a) Il metodo dell’“experience rating” è largamente
adottato con riferimento al “working layer”, per il
quale le esperienze di sinistrosità sono più
numerose ed affidabili
b) Il metodo dell’“exposure rating” è frequentemente in
uso con riferimento ai “layers” successivi, per i quali è
opportuno sfruttare le esperienze di sinistrosità relative
a portafogli più numerosi
Il premio di riassicurazione:
ALTRI METODI DI CALCOLO
¾ Metodi in uso ai fini del calcolo del premio (equo) della
riassicurazione “per event excess of loss” e soprattutto nel
caso di evento catastrofale
a) il “rate on line”
ottenuto rapportando alla portata globale del trattato
(supposto di durata annuale) i relativi premi annui
b) il “payback period ” reciproco del “rate on line”:
numero di anni necessari per recuperare, mediante l’introito
di premi costanti di riassicurazione, il cosiddetto “sinistro
totale” (vale a dire, un esborso per il riassicuratore eguale
alla portata globale del trattato).
Il premio di riassicurazione:
CARICAMENTO DI SICUREZZA (1/2)
¾ Il corrispondente margine applicato nella copertura
assicurativa di base costituisce soltanto un elemento di
riferimento per il calcolo di questa grandezza, anche nel
caso delle garanzie riassicurative proporzionali:
a) la cessione dei rischi in riassicurazione determina il
trasferimento al riassicuratore di utili attesi dall’assicuratore
in conseguenza a quest’ultimo (assicuratore) è riconosciuta
una provvigione di riassicurazione più o meno
consistente a seconda della forma riassicurativa adottata
Il premio di riassicurazione:
CARICAMENTO DI SICUREZZA (2/2)
b) le diverse forme di riassicurazione sono caratterizzate da
differenti livelli di esposizione al rischio del riassicuratore
esigenza, da parte di quest’ultimo (riassicuratore), di introdurre
differenti livelli di caricamento di sicurezza nel premio puro
c) la base statistica utilizzata dal riassicuratore per la
valutazione dei rischi riassicurati non necessariamente
coincide con quella adottata dall’assicuratore al momento
dell’assunzione dei medesimi rischi
Il premio di riassicurazione:
PROVVIGIONE DI RIASSICURAZIONE
¾ È di norma ottenuta in percentuale dei premi e può essere
determinata:
a) a priori: in tal caso si ha
una provvigione fissa
b) a posteriori: in tal caso si
ha una provvigione scalare
Le parti generalmente concordano una provvigione provvisoria
che viene inizialmente applicata e poi eventualmente adeguata
alla fine del rapporto riassicurativo
• Le formule adottate per il calcolo della provvigione scalare sono
basate tradizionalmente sull’andamento del rapporto percentuale sinistri
a premi di competenza del portafoglio
( e consentono di premiare l’assicuratore nel caso in cui l’onere per sinistri
osservato, in rapporto al volume dei premi incassati, sia stato inferiore alle attese)
Riassicurazione ed inflazione
¾ Nelle forme di riassicurazione non proporzionali occorre
anche tenere conto delle conseguenze dell’inflazione
• L’ inflazione può far sì che il risarcimento relativo ad un
sinistro che colpisce un contratto (o relativo ad una massa di
sinistri che colpiscono un portafoglio) superi, al momento
della liquidazione, la fissata priorità
(in particolare, se la liquidazione dei sinistri è notevolmente
differita nel tempo)
Clausola di stabilità
impegna l’assicuratore ad indicizzare il livello della sua ritenzione
adeguandolo nel tempo al potere d’acquisto della moneta
Riassicurazione ECOMOR
(“Excedent du COut MOyen Relatif” )
¾ Copertura riassicurativa non proporzionale, introdotta da
Thépaut (1950), che si prefigge di limitare le conseguenze
negative derivanti dall’inflazione
• Nell’ipotesi che i risarcimenti siano ordinati in senso non
crescente, la riassicurazione “E.CO.MO.R.” opera in modo
analogo alla riassicurazione “excess of loss”, con la differenza
che la priorità corrisponde ora al risarcimento relativo
all’m-esimo sinistro, per importo, che colpisce il portafoglio
Al riassicuratore sono pertanto trasferiti i risarcimenti eccedenti
tale priorità, riguardanti i primi (più grandi) m-1 sinistri
Riassicurazione ECOMOR
APPLICABILITÀ
¾ Ai fini della sua applicazione è necessario ordinare i
sinistri in base all’ammontare del relativo risarcimento
Y1:N ≥ Y2:N ≥ ... ≥ Yj:N ≥ ... ≥ YN:N
essendo i risarcimenti ordinati in senso non crescente
• OSSERVAZIONE
Il riferimento è l’intero portafoglio e non il singolo
contratto del portafoglio
(N: numero di sinistri che colpiscono il dato portafoglio)
9 Impostazione collettiva della teoria del rischio, alternativa
all’impostazione individuale della teoria del rischio
Riassicurazione ECOMOR:
RISARCIMENTO TRATTENUTO E
RISARCIMENTO CEDUTO
¾ Risarcimento globale conservato dall’assicuratore
X =
A
N
∑
j = m +1
Y j:N + mYm:N
¾ Risarcimento globale ceduto al riassicuratore
m
X = ∑ Y j:N − mYm:N
R
j =1
9 La priorità corrisponde al risarcimento, Ym:N
Riassicurazione ECOMOR:
ESEMPIO (1/2)
• In riferimento ad un portafoglio di assicurazioni contro i danni
contemporaneamente stipulate e di durata annuale si ipotizzi:
a) che i risarcimenti siano ordinati in senso non crescente
y1:k ≥ y2:k ≥ ... ≥ yj:k ≥ ... ≥ yk:k
si tiene conto, a posteriori, dei risarcimenti osservati:
k sinistri che nell’anno di copertura riassicurativa hanno colpito il dato portafoglio
b) che la priorità corrisponda al risarcimento, ym:k, m-esimo più
grande sinistro tra i k sinistri osservati, con m fissato all’inizio del
rapporto riassicurativo
c) che la distribuzione di probabilità del risarcimento, Y, sia
ben rappresentata da una distribuzione di Pareto di
parametro η (con η > 1) e θ = 1
FY ( y ) = 1 − y −η ,
y ≥1
funzione di ripartizione
Riassicurazione ECOMOR:
ESEMPIO (2/2)
¾ Premio equo di riassicurazione
P R = E ( X R ) = (m − 1) E[Y | Y > ym:k ] =
∫
= (m − 1)
+∞
y m:k
y −η dy
1 − FY ( ym:k )
= (m − 1)
ym:k
.
η −1
dipende anche dall’importo ym:k
(noto solo alla fine dell’anno di copertura riassicurativa)
9 Ai fini della determinazione del premio puro di riassicurazione, ad esempio
mediante il principio della varianza, occorre evidentemente che si abbia η > 2
Politiche ottimali di riassicurazione
¾ Un fondamentale aspetto dei profili attuariali della
riassicurazione per le assicurazioni contro i danni è rappresentato
dalla ricerca di una politica di ritenzione ottimale dei rischi
(o, anche, politica ottimale di riassicurazione) con riferimento
ad un portafoglio assicurato (in forma proporzionale o non
proporzionale, individuale o globale,…)
• Il problema può essere affrontato:
a) da un punto di vista dell’assicuratore, definendo così una
politica unilaterale di ritenzione ottimale dei rischi;
b) da un punto di vista dell’assicuratore e del riassicuartore,
definendo così una politica bilaterale di ritenzione
ottimale dei rischi.
Politiche unilaterali ottimali di riassicurazione
(1/3)
¾ Criteri di valutazione
(a) Criterio dell’utilità attesa;
(b) Criterio della probabilità di rovina.
(a) Criterio dell’utilità attesa
L’obiettivo dell’assicuratore consiste nella massimizzazione
dell’utilità attesa del guadagno aleatorio di portafoglio
(ex-post la riassicurazione) con riferimento ad un orizzonte
temporale di durata annuale
Ricerca dei valori delle variabili decisionali (aliquote di
conservazione, priorità) che massimizzano l’utilità attesa del
guadagno relativo al portafoglio riassicurato
Politiche unilaterali ottimali di riassicurazione
(2/3)
(b) Criterio della probabilità di rovina
L’obiettivo dell’assicuratore consiste nella minimizzazione
della varianza del guadagno aleatorio di portafoglio
(ex-post la riassicurazione) condizionatamente ad una
prefissata riduzione del guadagno atteso (di portafoglio)
conseguente alla riassicurazione
(con i rischi l’assicuratore cede anche parte dei relativi utili)
Ricerca delle aliquote di conservazione (non negative e non
superiori all’unità), in accordo al problema di ottimizzazione per
una politica unilaterale ottimale di riassicurazione (con il criterio
della probabilità di rovina) proposto da de Finetti (1940)
Politiche unilaterali ottimali di riassicurazione
(3/3)
¾ In accordo al problema di ottimizzazione proposto da de Finetti
a) Problema dei pieni relativi (di conservazione)
Ricerca delle aliquote di conservazione (non negative e non
superiori all’unità), che rendono minima la varianza del guadagno
aleatorio di portafoglio (ex-post la riassicurazione)
condizionatamente ad una prefissata riduzione del guadagno atteso
(di portafoglio) conseguente alla data garanzia riassicurativa
b) Problema dei pieni assoluti (di conservazione)
Ricerca delle aliquote di conservazione (non negative e non
superiori all’unità), condizionatamente ad una prefissata
probabilità di rovina, ε*, che l’assicuratore ritiene accettabile
(e che determina anche la conseguente riduzione di guadagno atteso
di portafoglio conseguente alla riassicurazione)
Politiche bilaterali ottimali di riassicurazione
(1/2)
¾ In accordo al problema di ottimizzazione proposto da
Benktander (1975)
• In base al criterio dell’utilità attesa, se l’assicuratore è più
avverso al rischio del riassicuratore, esiste un intervallo di
trattativa (intervallo di valori) che rende vantaggioso il
rapporto riassicurativo per entrambe le parti.
Intervallo di trattativa:
È compreso tra il premio di indifferenza del riassicuratore,
Π”, ed il premio di indifferenza dell’assicuratore, Π’
che è più alto perché l’assicuratore è (per ipotesi realistica)
più avverso al rischio del riassicuratore
Politiche bilaterali ottimali di riassicurazione
(2/2)
Π”
Π’
ΠR
Premio di riassicurazione
¾ È realistico pensare che l’assicuratore ed il riassicuratore
possano concordare su una garanzia che
- massimizzi la differenza Π’ - Π”;
- ripartisca al meglio la riduzione di varianza del risarcimento
globale conseguente alla decomposizione in risarcimento
trattenuto e risarcimento ceduto.
A cura di:
Chiara Parrini
[email protected]