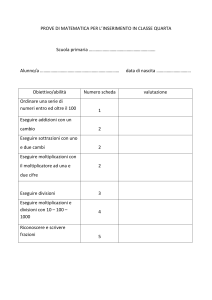
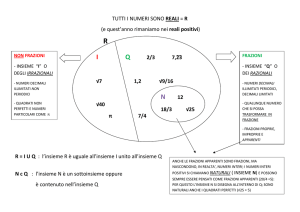
Matematica 3^
COMPETENZE ATTESE AL TERMINE DELLA CLASSE TERZA
L’ALUNNO:
domina la scrittura dei numeri naturali almeno entro le migliaia;
fa un uso consapevole delle operazioni aritmetiche;
riconosce le caratteristiche delle figure e distingue perimetro e area;
interpreta e costruisce grafici statistici;
valuta la possibilità o meno che un evento si verifichi;
compie misurazioni e confronta tra loro multipli e sottomultipli di una stessa unità di misura;
interpreta e gestisce situazioni problematiche.
SETTEMBRE: Prove d’ingresso e attività iniziali
OTTOBRE: ENTRO IL 1000, DALLO SPAZIO AL PIANO, PROBLEMI
OB. DI APPRENDIMENTO
CONTENUTI
ATTIVITÀ
Numeri
Numeri e cifre entro il
Giochiamo con le carte per
• Usare le cifre per comporre i
1000. Composizione e
far ragionare sul valore posinumeri entro il 1000.
scomposizione in base
zionale delle cifre. Con la ta• Contare in base 10.
10. La struttura del nubella dei primi 100 numeri e
• Riflettere sulla struttura dei
mero.
indovinelli, osserviamo e connumeri naturali e sul nostro
Simmetrie assiali. Fisolidiamo le regole del nostro
sistema numerico.
gure tridimensionali e
sistema di numerazione. ParSpazio e figure
figure bidimensionali.
tiamo da un gioco e poi
• Identificare simmetrie.
Situazioni problematiusiamo alcune piegature per
• Riconoscere e analizzare figure
che che richiedono più
comprendere tangibilmente
piane e solide.
operazioni.
che cosa voglia dire asse di
• Passare consapevolmente dalla
simmetria. Analizziamo figure
rappresentazione tridimensiosolide e piane. Prendiamo in
nale a quella bidimensionale e
considerazione situazioni proviceversa.
blematiche che richiedono più
Introduzione al pensiero
di una operazione per essere rirazionale
solte.
• Riflettere sul testo del problema per individuare l’obiettivo
da raggiungere.
NOVEMBRE: IL MIGLIAIO, MISURAZIONI LINEARI, GRAFICI
OB. DI APPRENDIMENTO
CONTENUTI
ATTIVITÀ
Numeri
Composizione e scomCon un gioco a squadre for• Comporre e scomporre i numeposizione dei numeri
miamo i numeri a quattro ciri in base 10: il migliaio.
oltre il 1000. Segni refre; usiamo anche l’abaco per
• Porre a confronto i numeri
lazionali aritmetici. Mivisualizzare composizione e
con l’uso dei segni > = <.
sure di lunghezza.
scomposizione; sul quaderno
Misura
Ideogrammi, aerocomponiamo, scomponiamo e
• Svolgere attività di misurazione
grammi quadrati e a
confrontiamo tra loro i numeri.
di lunghezze.
torta. Situazioni proPoniamo a confronto le altezRelazioni, dati e previsioni
blematiche.
ze dei bambini e confrontia• Organizzare, rappresentare e
mole con le misure neonatali.
interpretare dati.
Interpretiamo i dati di un
Introduzione al pensiero
ideogramma con i risultati di
razionale
un’inchiesta scolastica e poi
• Riflettere sul testo del protrasformiamo l’ideogramma in
blema e cercare diversi registri
un aerogramma quadrato.
semiotici per rappresentarlo.
Leggiamo una tabella delle
frequenze con le quali sono
proposti i piatti alla mensa e
passiamo all’elaborazione del
testo di una situazione problematica.
DICEMBRE: ADDIZIONI, PROBLEMI, MISURE LINEARI
OB. DI APPRENDIMENTO
CONTENUTI
ATTIVITÀ
Numeri
La tabella dell’addizioRiflettiamo sul rapporto che
• Scoprire e usare le proprietà
ne. Proprietà commulega tra loro i numeri
dell’addizione per calcolare.
tativa e associativa delnell’addizione. Analizziamo la
• Eseguire addizioni in riga e in
l’addizione. L’algoritmo
proprietà commutativa e ascolonna con e senza riporto.
dell’addizione: il riporto.
sociativa dell’addizione. PoIntroduzione al pensiero
Situazioni problemaniamo particolare attenzione
razionale
tiche.
al riporto. In situazioni pro• Risolvere situazioni problemaMultipli e sottomultiblematiche, cerchiamo le intiche con l’algoritmo
pli del metro. Equivaformazioni utili per elaborare
dell’addizione.
lenze.
una soluzione. Approfondiamo
Misura
Punto, retta, linea.
la conoscenza e l’uso dei sot• Riconoscere e usare multipli e
tomultipli e multipli del metro
sottomultipli del metro.
e svolgiamo attività di misu• Esprimere espressioni equivarazione. Accostiamoci al punlenti delle misure di una stessa
to, alla linea e alla retta senza
grandezza.
arrivare a definizioni nette.
Spazio e figure
Proponiamo situazioni proble• Riconoscere gli enti della geomatiche che richiedono conmetria.
creti atti di misurazione e pos• Risolvere problemi legati alla
sono essere risolte con algoritmi
misurazione di lunghezze.
di calcolo ed equivalenze.
GENNAIO: SOTTRAZIONI, FRAZIONI, LINEE, PROBLEMI – VERIFICHE INTERMEDIE
OB. DI APPRENDIMENTO
CONTENUTI
ATTIVITÀ
Numeri
Proprietà invariantiva
Proponiamo situazioni dove
• Scoprire e usare la proprietà
della sottrazione. Tasia necessario ricercare la diffeinvariantiva della sottrazione
bella della sottrazione.
renza, il resto e il complemenper calcolare.
Sottrazione e addiziotare di un numero. Riflettiamo
• Creare la tabella della sottrane: operazioni inverse.
sulla proprietà invariantiva
zione e ragionare sulle regole
Sottrazioni in riga e in
della sottrazione. Eseguiamo
per comporla.
colonna con i cambi.
esercizi per imparare a gestire
• Eseguire sottrazioni in riga e
Le frazioni. L’istogramin riga l’algoritmo della sottrain colonna anche con uno o
ma. La moda. Rette,
zione. Eseguiamo sottrazioni
più prestiti.
semirette e segmenti.
in colonna, con uno e due
• Riflettere sul termine frazione in
Rette incidenti e paralcambi. Avviciniamoci alla framatematica.
lele. Regione interna
zione, lavorando per ora, solo
Relazioni, dati e previsioni
ed esterna.
con grandezze continue. Inter• Organizzare, rappresentare e
pretiamo e creiamo istograminterpretare dati in istogrammi e accostiamoci al concetto
mi.
di moda. Riflettiamo sul fatto
Spazio e figure
che nella realtà non esistono
• Conoscere i concetti
rette, semirette e segmenti.
d’incidenza e parallelismo.
• Tracciare rette, semirette,
segmenti e riconoscerne la reciproca posizione.
FEBBRAIO: MOLTIPLICAZIONI, MISURE DI PESO, ANGOLI
OB. DI APPRENDIMENTO
CONTENUTI
ATTIVITÀ
Numeri
Proprietà commutatiScopriamo le proprietà della
• Conoscere e usare le proprietà
va e associativa della
moltiplicazione e conquistiamo
commutativa e associativa delmoltiplicazione. Moltimaggiore padronanza della
la moltiplicazione.
plicazioni in riga e in
moltiplicazione in colonna.
• Sperimentare diverse tecniche
colonna con il cambio.
Scopriamo divertenti modi di
d’esecuzione di moltiplicazioNumeri come somma
eseguire moltiplicazioni anche
ni.
prodotti.
senza conoscere le tabelline.
• Eseguire moltiplicazioni in riga
Multipli e sottomultipli
Procuriamoci una bilancia a
e in colonna con e senza ripordel grammo. Equivapiatti e una serie di pesi e facto.
lenze.
ciamo esperienza di pesatura,
• Riflettere sul sistema posizionale
Moda e mediana. Gli
stima, confronti, fino a elabodei numeri.
angoli.
rare una tabella dei multipli del
Misura
Problemi.
grammo. Proponiamo alcuni
• Riconoscere multipli e sottografici riguardanti la vita della
multipli del grammo.
scuola e calcoliamo media e
• Usare e confrontare misure di
mediana. Esploriamo
peso.
l’ambiente alla ricerca di an• Scoprire analogie tra i sistemi
goli. Impariamo a riconoscerli,
di misurazione di peso e lineainiziamo a fare alcune misurare con il sistema posizionale
zioni, denominiamoli e poi
delle cifre.
cominciamo a confrontare le
Relazioni, dati e previsioni
loro ampiezze. Proponiamo al• Riconoscere indicatori statistici:
cune situazioni problematimedia e mediana.
che legate alla quotidianità.
Spazio e figure
• Riconoscere gli angoli, definirli
e misurarne le ampiezze.
Introduzione al pensiero
razionale
• Risolvere situazioni problematiche con moltiplicazioni e con
gli altri algoritmi di calcolo conosciuti.
• Risolvere situazioni problematiche legate alle misure di peso.
MARZO: NUMERI A CINQUE CIFRE, MISURE DI CAPACITÀ, ANGOLI, QUADRATI
E RETTANGOLI, FRAZIONI
OB. DI APPRENDIMENTO
CONTENUTI
ATTIVITÀ
Numeri
• Eseguire moltiplicazioni per 10,
100, 1000.
• Analizzare il valore posizionale
nella composizione e scomposizione di numeri a cinque
cifre.
• Riconoscere l’unità frazionaria.
• Riconoscere frazioni complementari.
Spazio e figure
• Descrivere, confrontare disegnare e misurare angoli.
• Analizzare le caratteristiche di
quadrati e rettangoli e trovare
Moltiplicazioni per 10,
100 e 1000.
Composizione e scomposizione dei numeri
oltre il 1000.
Unità frazionaria. Frazioni e frazioni complementari.
Angoli, quadrati e rettangoli.
Multipli e sottomultipli
del litro.
Equivalenze. Diagramma di flusso. Situazioni problema-
Prendiamo spunto da una storia per vedere che cosa succede quando moltiplichiamo un
numero per 10, 100 e 1000.
Scomponiamo un numero
come somma di prodotti. Invitiamo a dividere e colorare
le superfici di fogli millimetrati
e confrontiamo le diverse
suddivisioni, per riconoscere
che cosa significa frazionare
un’unità continua. Lavoriamo
con frazioni complementari.
Creiamo uno strumento per la
comparazione delle ampiezze.
differenze e analogie.
tiche.
Con righello e squadra diseMisura
gniamo rappresentazioni di
• Usare e confrontare misure di
quadrati e rettangoli e scocapacità.
priamo differenze e analogie.
• Riconoscere multipli e sottoCompiamo prove concrete di
multipli del litro.
misurazione dei liquidi. Fac• Esprimere espressioni equivaciamo prime tangibili equivalenti alle misure di una stessa
lenze. Analizziamo la succesgrandezza.
sione delle azioni in un evenRelazioni, dati e previsioni
to usando il diagramma di
• Analizzare la successione delflusso. Abituiamo i bambini a
le azioni e metterle in ordine.
verificare che il risultato di
Introduzione al pensiero
una soluzione sia coerente con
razionale
il testo della situazione pro• Risolvere situazioni problemablematica presentata.
tiche con misure di capacità.
• Verificare in situazioni problematiche se il risultato ottenuto
dalla soluzione sia coerente
con il testo e la domanda del
problema.
APRILE: DIVISIONI, NUMERI DECIMALI, EQUIVALENZE, POLIGONI
OB. DI APPRENDIMENTO
CONTENUTI
ATTIVITÀ
Numeri
Divisioni e moltiplicaScriviamo le tabelline della di• Mettere in relazione divisione
zioni a confronto. Provisione, ponendole in relazioe moltiplicazione.
prietà invariantiva della
ne con quelle della moltiplica• Conoscere e usare tecniche di
divisione.
zione. Ragioniamo sui risultati,
calcolo.
Frazioni e numeri deciscriviamo le nostre scoperte
• Conoscere e usare la proprietà
mali. Equivalenze con
poi riproduciamo il lavoro sui
invariantiva della divisione.
numeri decimali. Poliquaderni. Scopriamo che usa• Mettere in relazione frazioni
goni. Triangoli. Sire le frazioni decimali o i
decimali e numeri decimali.
tuazioni problematiche
numeri decimali è un modo
Misura
con la divisione.
diverso di scrivere le stesse
• Usare e confrontare misure: le
quantità. Consolidiamo e acequivalenze tra misure espresquisiamo una maggiore consase con numeri decimali.
pevolezza nel calcolare misure
Spazio e figure
equivalenti. Offriamo diffe• Porre a confronto poligoni e
renti situazioni che tengano
ricercarne le principali caratteconto della diversità semantiristiche.
ca caratteristica dei problemi
• Analizzare e confrontare le
di divisione. Identifichiamo fiprincipali peculiarità dei triangure geometriche e troviamo
goli.
analogie e differenze. LavoIntroduzione al pensiero
riamo con i triangoli per ricorazionale
noscerli e catalogarli in base
• Risolvere problemi con la divialle caratteristiche dei lati e
sione e gli altri algoritmi di
degli angoli.
calcolo conosciuti.
MAGGIO: MISURE MONETARIE, PERIMETRI, PROBLEMI – VERIFICHE FINALI
OB. DI APPRENDIMENTO
CONTENUTI
ATTIVITÀ
Registriamo le variazioni che
Numeri
Divisioni per 10, 100 e
avvengono in un numero ogni
• Eseguire divisioni nei numeri
1000.
volta che è diviso per 10, 100
naturali per 10, 100 e 1000.
L’Euro.
e 1000. Apriamo uno spor• Applicare la conoscenza dei
Perimetro. Isoperimetello bancario: usiamo il facnumeri decimali alle misure
tria ed equiestensione.
monetarie correnti.
Spazio e figure
• Calcolare il perimetro delle figure piane più note.
• Ragionare sui problemi di isoperimetria ed equiestensione.
Relazioni, dati e previsioni
• Riflettere sulla prevedibilità dei
fatti.
Introduzione al pensiero
razionale
• Risolvere situazioni problematiche.
Eventi e loro prevedibilità.
Problemi.
simile del denaro, costruiamo
una tabella con i valori monetari, elaboriamo cambi, facciamo confronti e passiamo
dalla scrittura con le frazioni a
quella decimale e viceversa ➜
CITTADINANZA ATTIVA.
Proponiamo la misurazione del
perimetro. Cominciamo a
parlare di isoperimetria ed
equiestensione. Analizziamo il
significato di evento, certo,
possibile, impossibile.