Problema 1
Un pendolo semplice, di massa m1 = 0.1 kg e lunghezza l = 0.8 m, è tenuto in equilibrio ad un angolo
θ0 = 30° rispetto alla verticale da una forza orizzontale F. Calcolare:
a) il modulo di F;
b) la tensione N del filo.
Si rimuove F ed il corpo è lasciato libero. Calcolare:
c)
d)
e)
f)
g)
la velocità massima vmax del pendolo;
il primo istante temporale tvmax al quale si verifica la velocità massima vmax;
l’accelerazione massima amax del pendolo;
il primo istante temporale tamax al quale si verifica l’accelerazione massima amax;
La tensione massima Nmax del filo.
Dopo essere passato per la posizione verticale, quando il pendolo ha un angolo di 10° rispetto alla
verticale, viene istantaneamente tagliato il filo. Sapendo che nella posizione verticale la massa si trova
ad una quota h = 0.5 m, calcolare:
h) la velocità v10° della massa quando viene tagliato il filo del pendolo;
i) l’altezza massima hmax raggiunta dalla massa.
Soluzione:
a)
cos
=
=
tan
=
cos
sin
= 0.58
b)
+
sin
= 1.14
c)
=
2
1 − cos
d)
% & =
' cos '& + (
Perché % & sia massima:
|cos '& + ( | = 1
'& + ( = *
*
(=
2
' = + = 3.5" #$
= 1.46 " #$
&=
e)
*
= 0.45"
2'
| = |−'.
|-
| = 5.14 " #.
f)
L’accelerazione massima si ha agli estremi, quindi &
=0
g)
=
+
.
= 1.25
h)
$ °
=
2
cos 10 − cos
= 1.37 " #$
i)
$ °,2
ℎ
=
$ ° sin 10
= 0.24 " #$
= ℎ + 1 − cos 10 +
2
10,4
2
= 0.52
Problema 2
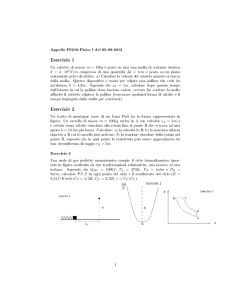
Un corpo di massa m = 2 kg scivola lungo un piano liscio (senza attrito), inclinato di θ = 5°; esso parte
con velocità nulla dal punto A e percorre lungo il piano la distanza d = 4 m. Calcolare:
a) il tempo tB al quale il corpo giunge nel punto B;
b) la velocità vB con la quale il corpo giunge nel punto B.
Alla fine del piano inclinato, il corpo si muove per un tratto orizzontale lungo l = 2 m e urta una molla
di lunghezza a riposo x0 = 5 cm, fissata ad un muro. Calcolare, nel caso in cui nel tratto orizzontale non
vi sia attrito tra la superficie e il corpo e nel caso in cui invece vi sia attrito, con un coefficiente di
attrito dinamico µd = 0.14:
c) il tempo tC al quale il corpo giunge nel punto C (posto immediatamente prima dell’estremità
della molla);
d) la velocità vC con la quale il corpo giunge al punto C;
e) quanto deve valere la costante elastica della molla affinché la molla venga compressa di 4 cm.
Infine calcolare:
f) quanto dovrebbe valere µd per fare in modo che il corpo arrivi nel punto C con velocità nulla.
m
x0
θ
A
C
B
d
l
Soluzione
b)
ℎ = 5 sin
0.35
Conservazione dell’energia tra il punto A e il punto B:
1
2
3
2 3
6
a)
5
&6
.
6
2.62 " #$
1
sin &6.
2
7
25
sin
0.35
3.06"
Caso senza attrito:
c)
&6#8
&8
6 &6#8
6
3.82"
0.76"
d)
6
e)
8
2.62 " #$ 1
2
.
9
1
= :∆< .
2
.
8
∆< .
:=
= 8580.5 #$
Caso con attrito:
c)
=
6 &6#8
1
.
− => &6#8
2
&6#8 = 1.06"
&8 = 4.12"
d)
8
=
6
− => &6#8 = 1.16 " #$ e)
1
2
.
8
:=
1
= :∆< .
2
.
8
∆< .
= 1682 =
=>
#$
f)
1
2
.
6
=> =
1
2
.
6
= 0.175
Problema 3
Una pallina di piombo (cp = 0.128 J g-1 K-1) di massa m = 0.1 kg viene lasciata cadere da un’altezza h =
10 m dal suolo. Tralasciando l’attrito dell’aria e assumendo che come effetto dell’urto con il suolo
tutta l’energia sia dissipata sotto forma di variazione dell’energia interna della sola pallina,
determinare:
a) l’incremento della temperatura della pallina stessa;
b) quale è la dipendenza dell’incremento di temperatura dalla massa della pallina;
c) da che quota dovrebbe essere lanciata la pallina per avere un incremento di temperatura di
1°C.
Soluzione
a)
ℎ=
∆A =
?@ ∆A
ℎ
9.81 ∙ 10
=
= 0.77E
?@ 0.128 ∙ 10D
b)
Si osserva che la variazione di temperatura risulta indipendente dalla massa della pallina.
c)
ℎ=
∆A?@
=
1 ∙ 0.128 ∙ 10D
= 13.05
9.81