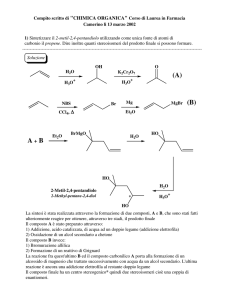
1
CHIMICA
Ing Edile e Architettura
Programma della II Prova in itinere
Anno 2007-2008
STATO SOLIDO
Le strutture cristalline di riferimento per l’esame sono:
Cristalli ionici tipo NaCl, CsCl, ZnS (blenda), CaF2 (fluorite), CaTiO3 (perowskite),
Cristalli covalenti tipo C(diamante), Si, Ge,
Metalli (in particolare Feα e Feγ)
Nei problemi si puo’ richiedere di disegnare queste celle e di eseguire sulle stesse calcoli
stechiometrici come illustrato negli esempi di seguito riportati.
Il programma comprende anche una conoscenza qualitativa delle strutture covalenti del quarzo e
della grafite
Problema 1
- Determinare la “formula” e il peso della cella elementare di CaO che ha una struttura tipo NaCl.
Disegnare la cella: cella cubica a facce centrate di ioni O2- con gli ioni ossido Ca2+ che occupano i siti
ottaedrici (centro degli spigoli e centro della cella):
Ricordando che, per effetto delle condivisioni con le celle contigue, le posizioni di vertice contano per 1/8,
quelle al centro delle facce per ½ , quelle al centro degli spigoli per ¼ , quelle interne alla cella per 1
numero ioni O2- = 8x1/ 8 + 6x1/2 = 4
numero ioni Ca2+= 12x1/4 + 1 = 4
Formula della cella : Ca4O4, ovvero, 4CaO
PF(CaO) =56.1 μ, mole CaO = 56.1 (g/mole)
Peso cella = 4x56.1/6.022x1023 = 3.73x10-22 g
Problema 2
descrivere la cella elementare del Feα e calcolarne lo spigolo in cm
dato: densita’ del Feα = 7.86 g/cm3.
Cella cubica a corpo centrato (disegnare)
Numero atomi di Fe = 8x1/8 + 1=2. Peso cella = 55.8x2/6.022x1023 = 1.85x10-22 g
Dalla relazione: densita’ = (peso cella)/(volume cella):
Vcella = 1.85x10-22/7.86 =2.36x10-23 cm3
Spigolo cella = (Vcella)1/3 = (2.36x10-23)1/3 = 2.86x10-8 cm
Problema 3
A -Descrivere la cella elementare del Feγ mettendo in evidenza i siti tetraedrici e ottaedrici;
Cella c.f.c ( disegnare); i siti ottaedrici sono al centro degli spigoli e al centro della cella; i siti tetraedrici
sono al centro delle otto sottocelle cubiche che si ottengono dividendo la cella con 3 piani perpendicolari tra
di loro e alle facce della cella
B-Gli atomi di C possono entrare nei siti ottaedrici della cella del Feγ dando luogo a soluzioni solide
interstiziali denominate austeniti
- Calcolare la % di C nella cella del Feγ supponendo che tutti i siti ottaedrici siano occupati
Gli atomi di C occupano il centro degli spigoli e il centro della cella
Numero atomi di Fe = 8x1/8 + 6x1/2 = 4
Numero atomi di C = 12x1/4 + 1= 4
Formula della cella. Fe4C4; mole di Fe4C4 = 271.2 g/mole
% di C = [(12.0x4)/271.2] x100 = 17.7 %
In realta’, a causa dell’accumulo delle tensioni nella struttura cristallina, gli atomi di C possono
occupare non piu’ di ca 1/10 dei siti ottaedrici, corrispondente ad una concentrazione di C =
2.07% (Austenite satura a T = 1147 °C)
Problema 4
Disegnare la cella elementare del C(diamante) e calcolarne lo spigolo in cm .
Dato: densita’ del C(diamante) = 3.51g/cm3
2
Il diamante cristallizza con una cella cubica nella quale sono occupate le posizioni dei vertici e del centro
delle facce e meta’ dei siti tetraedrici interni (ovvero, cella c.f.c. di atomi di C nella quale altri 4 atomi di C
occupano meta’ dei siti tetraedrici interni)..
Calcolo del numero di atomi di C nella cella: (8x1/8 ) + 6x(1/2) + 4 = 8 atomi di C
Peso della cella: (8x 12.011) /6.022x1023 = 1.5956x10-22 g
Volume della cella= peso/densita’ = 1.5956x10-22 (g)/ 3.51(g/cm3) = 4.5459x10-23 (cm3)
Spigolo della cella = (V)1/3 = (4.5459x10-23)1/3 = 3.5689x10-8 cm
Problema 5
La densita’ e lo spigolo della cella del carbonio diamante, misurati sperimentalmente, sono rispettivamente
d = 3.51g/cm3 e l= 3.5689 x10-8 cm: calcolare il numero di Avogadro
Schema di procedimento:
Calcolo del volume della cella dallo spigolo Æ calcolo del peso della cella dalla relazione: peso = volume x
densita’ Æ calcolo del numero di atomi di C nella cella Æ calcolo del numero di atomi presenti in una
mole di carbonio diamante (numero di Avogadro)
Volume della cella, Vcella = l3 = 4.5459x10-23 cm3
Peso cella = Vcellax d = 1.5956 x10-22 g
Calcolo del numero di atomi di C nella cella: (8x1/8 ) + 6x(1/2) + 4 = 8 atomi di C
Mole di C = 12.011 g
Proporzione: 1.5956x10-22 : 8 = 12.011 : Nav
Nav = (8x12.011)/ 1.5956x10-22 = 6.022x1023
---------------------------------------------------------------------------------------------------------------------------------
EQUILIBRI DI FASE: Calcoli numerici con l’equazione di Clapeyron sugli equilibri liquidovapore e solido-vapore.
Problema 1
la pressione di vapore di un liquido e’ pari a 1.5 atm a 100 °C e 2.5 atm a 200 °C: calcolare
l’entalpia di evaporazione ΔHev
SOLUZIONE:
Equazione di Clapeyron: ln
P2 ΔH v ⎡ 1 1 ⎤
=
⎢ − ⎥
P1
R ⎣ T1 T2 ⎦
R = 8.314 (jxmole-1K-1)
Introducendo P1 = 1.15 atm , T1 = 373.1 K; P2 = 2.5 atm, T2 = 473.1 K
Risolvendo rispetto a ΔHv :
ΔHv = 7496.4 (J)
Problema 2
L’acqua bolle a 100 °C alla pressione di una atmosfera e ha un’entalpia di evaporazione ΔHev pari a
10.5 kcal/mole: calcolare la pressione di vapore a 150 °C
Soluzione:
Introducendo nell’equazione di Clapeyron P1=1 atm, T1 = 373.1 K; P2 = ?, T2 = 423.1 K R = 1.986 cal x
mole-1x K-1 e risolvendo rispetto a P2 : P2 = 5.33 atm
Problema 3
La pressione di vapore del alcol etilico e’P1 = 10 torr a -2.3° e P2 = 40 torr a 19°: calcolare la temperatura di
ebollizione dell’alcol etilico
Soluzione:
Schema di procedimento: da (P1,T1 ) e (P2,T2 ) Æ ΔHv ; da (P1,T1 ) e ΔHv con P2 = 760 torr Æ Teb
Dall’equazione di Clapeyron con P1= 10 torr, T1 = 270 (K); P2 = 40 torr, T2 = 292 (K) e ponendo R = 8.314
(Jmole-1K-1) si ottiene: ΔHv = 4.270x104 J/mole
Dall’equazione di Clapeyron con P1= 10 torr, T1 = 270 (K); P2 = 760 torr; ΔHv = 4.270x104 J/mole e R =
8.314, si calcola Teb = 350.8
3
REAZIONI ACIDO-BASE, CALCOLI SUL pH
Definizioni e richiami
Dissociazione di acidi deboli e forti in soluzioni acquose.
Esempi di acidi forti (completamente dissociati, Ka >>1)): HNO3, HCl, HBr, HI, HClO3, HClO4,
H2SO4 (quest’ultimo solo in soluzioni diluite)
HNO3 + H2O Æ H3O+ + NO3- Ka>> 1
Esempi di acidi deboli:
H2CO3 (acido carbonico, biprotico), HF( acido fluoridrico), HCN (acido cianidrico), CH3COOH
(acido acetico e tutti gli acidi carbossilici), HClO ( acido ipocloroso), HClO2 (acido cloroso),
H2SO3 (acido solforoso), HNO2 (acido nitroso)
HF + H2O ÅÆ H3O+ + FCationi generati da basi deboli: NH4+, cationi dei metalli di transizione e dei gruppi 3°, 4°, 5°
NH4+ +H2O ÅÆ NH3 + H3O+ ; Fe3+ + H2O ÅÆ Fe(OH)2+ + H+; FeOH+ + H2O ÅÆ Fe(OH)2+ +
H+; Fe(OH)2+ ÅÆ Fe(OH)3 + H+
Dissociazione di basi deboli e forti in soluzioni acquose
Esempi di basi forti(completamente dissociate):
idrossidi dei metalli del 1° e 2° gruppo:
LiOHÆ Li+ + OH- ; NaOH Æ Na+ + OH-; KOH Æ K++ OH-; RbOH Æ Rb+ + OH-; CsOH Æ Cs+ + OH-;
Ca(OH)2 Æ Ca2+ + 2 OH-; Ba(OH)2 Æ Ba2+ + 2 OH-; SrOH)2 Æ Sr2+ + 2 OH-
Esempi di basi deboli( parzialmente dissociate):
idrossidi dei metalli di transizione e dei gruppi 3°, 4°,5°
Fe(OH)3 ÅÆ Fe(OH)2+ + OHFe(OH)2+ ÅÆ Fe(OH)2+ + OHFe(OH)2+ ÅÆ Fe3+ + OHAmmoniaca e ammine organiche: NH3 + H2O ÅÆ NH4+ + OHProblema 1
- Calcolare il pH delle seguenti soluzioni acquose:
a) soluzione contenente 0.01 g di Ca(OH)2 in 300 cm3
Soluzione:
Dissociazione elettrolitica in acqua: Ca(OH)2 Æ Ca2+ + 2 OHP.F. (Ca(OH)2) = 74.0
Moli di Ca(OH)2 in 0.01 g = 0.01/74.0 = 1.35 x10-4
Concentrazione analitica di Ca(OH)2 = 1.35x10-4 (moli)/ 0.3 (L) = 4.50x10-4moli/L
Concentrazione molare di OH- = [OH-] =2 x 4.50x10-4 = 9.0x10-4 M
pOH = -log [OH-] = -log 9.0x10-4 =3.04
pH = 14 – pOH = 10.95
Problema 2
Calcolare il pH di una soluzione 0.15 M di H2SO4
Soluzione:
Dissociazione graduale dell’acido in acqua (soluzioni diluite, dissociazione quasi completa):
H2SO4 + H2O Æ H3O+ + HSO4HSO4- + H2O Æ H3O+ + SO42----------------------------------------H2SO4 + 2 H2O Æ 2 H3O+ + SO42Concentrazione molare di H3O+ = [ H3O+] = 2 x 0.15 = 0.3 M
pH = -log [ H3O+] = -log 0.3 = 0.52
Problema 3
data una soluzione acquosa di acido acetico CH3COOH di concentrazione C(CH3COOH) = 0.15 M e la
costante di dissociazione Ka = 1.8x10-5 , calcolarne il pH.
4
Soluzione:
CH3COOH + H2O ÅÆ CH3COO- + H3O+
[CH COO ][H O ]
Ka =
−
3
+
3
[CH 3COOH ]
Approssimazioni: a) [CH3COO ] ≅ [H3O ] ; b) [CH3COOH] ≅ CCH3COOH - [H3O+]
N.B. l’approssimazione b) si ricava dal bilancio di materiale
CCH3COOH = [CH3COO-] + [CH3COOH] ≅ [H3O+] + [CH3COOH]
-
+
Sostituendo nell’equazione della costante: Ka =
[H O ]
− [H O ]
+ 2
3
C CH 3COOH
+
3
Sviluppando: [H3O+]2 + Ka[H3O+] -KaCCH3COOH = 0
Soluzioni:
[H3O+]1 = 1.63x10-3 M; [H3O+]2 = -1.65x10-3 M
La seconda soluzione viene scartata perche’ non ha significato fisico
pH= -log 1.63x10-3 2.788
N.B. nel denominatore dell’equazione della Ka , [H3O+] << C(CH3COOH) ; percio’ l’equazione per il calcolo
del pH puo’ essere ulteriormente semplificata:
1/2
-3
[H3O+] = (Ka x C(CH3COOH)) =1.64x10 ; pH= 2.785
Problema 4
Calcolare il pH di una soluzione contenente 10 g di H3PO4 in 1.5 litri . Le costanti acide sono:
Ka1= 7.1x10-3, Ka2= 6.2x10-8, Ka3= 4.2x10-13
Soluzione:
PM(H3PO4) = 98.0
Moli di H3PO4 = 10 /98.0 = 0.102
Concentrazione analitica di H3PO4 , CH3PO4 = 0.102/1.5 = 0.068 (moli/L)
Dissociazione graduale dell’acido
H3PO4 +H2O ÅÆ H2PO4- + H3O+ Ka1= 7.1x10-3
H2PO4- +H2O ÅÆ HPO42- + H3O+ Ka2= 6.2x10-8
HPO42-+H2O ÅÆ PO43- + H3O+ Ka3= 4.2x10-13
Assumendo che Ka2 e Ka3 siano trascurabili rispetto a Ka1 e che sia trascurabile anche il contributo alla
concentrazione di H3O+ dell’autoprotolisi dell’acqua, il problema si risolve sulla base
[H PO ][H O ] = K
dell’equazione:
−
2
+
4
3
[H 3 PO4 ]
a1
Approssimazioni: a)[H2PO4-] ≅ [H3O+] ; b)[H3PO4] ≅ CH3PO4 - [H3O+]
[H O ]
=K
Sostituendo :
[C
] − [H O ]
+ 2
3
+
Sviluppando : [
H 3 PO 4
H3O+ 2
a1
3
] + Ka[H3O+] -KaCH3PO4 = 0
[H3O+]1 = 1.87x10-2
;
[H3O+]2 = - 2.58x10-2 ( da scartare)
pH = 1.728
N.B. nel denominatore dell’equazione della Ka , [H3O+] << CH3PO4; percio’ si puo’ semplificare
ulteriormente l’equazione per il calcolo del pH:
[H3O+] = (Ka x CH3PO4 )1/2= 2.197x10-2
pH= 1.66
errore dell’approssimazione ≅ 17.5 % ; l’approssimazione e’ praticabile con Ka non superiori a 10-4
Problema 5
Calcolare il pH di una soluzione acquosa di ammoniaca NH3 di concentrazione CNH3 = 0.2 M.
Dato: Kb = 1.8x10-5
Solzuaione:
L’ammoniaca e’ una base nei confronti dell’acqua: NH3 + H2O ÅÆ NH4+ + OH-
5
[NH ][OH ] = K
+
−
4
[NH 3 ]
b
Approssimazioni: a) [NH4+] ≅ [OH-] ; b) [NH3] ≅ CNH3 - [OH-]
[OH ]
− [OH ]
− 2
Sostituendo: Kb =
C NH 3
−
Æ
[OH-]2 + Kb[OH-] - KbCNH3 = 0
[OH-]1=1.89x10-3; [OH-]2 = -1.91x10-3
pOH = -log 1.89x10-3 = 2.723;
pH = 14-pOH = 11.277
N.B. nel denominatore dell’equazione della Kb , [OH ] << CNH3; percio’ si puo’ semplificare
ulteriormente l’equazione per il calcolo del pH:
[OH-] = (Kb x CNH3 )1/2= 1.90x10-3M;
pOH=2.721; pH=11.279
Problema 6
Il pH di una soluzione acquosa di NaOH e’ 12.5: calcolare il peso di HNO3 necessario per portare a
7 il pH di 150 cm3 di questa soluzione
Soluzione:
Si imposta la reazione di neutralizzazione NaOH + HNO3 Æ NaNO3 +H2O
pOH =14-pH = 1.5
[OH-] = 10-pOH = 10-1.5= 3.16x10-2 (moli/L)
Dalla stechiometria della dissociazione NaOH Æ Na+ + OH- si ha:[OH-] = CNaOH= 3.16x10-2 (moli/L)
150 cm3 = 0.15 L
moli di NaOH in 0.15 (L) = V(L) x CNaOH = 3.16x10-2 x 0.15 = 4.74x10-3
Dalla stechiometria della reazione: moli NaOH = moli HNO3 = 4.74x10-3
PM(HNO3) = 63.0
Peso di HNO3 = 4.74x10-3 x 63.0 = 0.2986 (g)
Reazioni acido-base di cationi e anioni (idrolisi)
- Scrivere le reazioni che giustificano il carattere basico di una soluzione acquosa di Na2CO3.
Dato: l’acido carbonico e’ un acido debole con costanti Ka1 = 4.3x10-7, Ka2 = 5.6x10-11
Dissociazione elettrolitica del sale in soluzione acquosa: Na2CO3 Æ 2 Na+ + CO32Carattere acido del catione e basico dell’anione:
- Na+ viene da una base forte (NaOH), il suo carattere acido e’ trascurabile
- CO32- viene da una acido debole, il suo carattere basico e’ percio’ significativo
Reazione dell’anione come base rispetto a H2O
1) CO32- + H2O ÅÆ HCO3- + OH- Kb1= 1.78x10-4
La reazione si puo’ interpretare come somma delle reazioni:
CO32- + H+ ÅÆ HCO32 H2O
ÅÆ H3O+ + OH----------------------------------CO32- + H2O ÅÆ HCO3- + OHLe dissociazioni dell’acido carbonico sono:
H2CO3 + H2O ÅÆ H3O+ + HCO3Ka1= 4.3x10-7
2+
HCO3 + H2O ÅÆ H3O + CO3
Ka2= 5.6x10-11
La Kb1 dell’equilibrio si correla con la Ka2 attraverso l’equazione: Kb1= Kw/Ka2 = 1.78x10-4
L’anione HCO3- e’ anfotero perche’ puo’ dar luogo contemporaneamente agli equilibri di dissociazione
basica e acida:
2) HCO3- + H2O ÅÆH2CO3 + OHKb2= Kw/Ka1 = 2.32x10-8
+
3) H2CO3 + H2O ÅÆ H3O + HCO3 Ka2= 5.6x10-11
Problema 7
Data una soluzione di Na2CO3 con concentrazione analitica CNa2CO3 = 0.1 M e le Ka dell’acido carbonico,
calcolare il pH.
Le Ka dell’acido carbonico sono: Ka1= 4.3x10-7; ka2=5.6x10-11;
Poiche’ Kb1>> Kb2,Ka2, il calcolo del pOH si imposta sulla sola reazione 1
6
[HCO ][OH ] = K
[CO ]
−
−
3
2−
b1
= 1.78x10-4
3
Approssimazioni: [HCO3-] ≅[ OH-] ; [CO32-] ≅ [H2CO3]
[OH-] = ( Kb1x CNa2CO3)1/2 = 4.2x10-3 pOH = -log 4.2x10-3 = 2.37 ;
pH = 14-pOH = 11.62
Problema 8: Scrivere le reazioni che giustificano il carattere acido di una soluzione acquosa di
solfato ferroso FeSO4
N.B. l’idrossido ferroso Fe(OH)2 e’ una base debole
Dissociazione elettrolitica in soluzione acquosa: FeSO4 Æ Fe2+ + SO42Carattere acido del catione :
- Fe2+ viene da una base debole, Fe(OH)2, il suo carattere acido e’ percio’ significativo
- SO42- viene da una acido forte, il suo carattere basico e’ trascurabile
Reazione del catione come acido verso H2O:
Fe(H2O)62+ + H2O ÅÆ [Fe(H2O)5(OH)]+ + H3O+
[Fe(H2O)5(OH)]+ + H2O ÅÆ[Fe(H2O)4(OH)2] + H3O+
2+
Il catione Fe si trova in soluzione nella forma idrata Fe(H2O)62+ . Le reazioni avvengono tra le molecole di
H2O legate al metallo piu’ acide) e quelle libere in soluzione.
---------------------------------------------------------------------------------------------------------------------------------PRODOTTO DI SOLUBILITA’
N.B.
Un solido si scioglie in un liquido sino a raggiungere una concentrazione massima detta di saturazione.
Questa concentrazione limite e’ la conseguenza di un equilibrio dinamico fra il solido presente come corpo
di fondo e le sue particelle costitutive (ioni, molecole) in soluzione. La costante di questo equilibrio e’
convenzionalmente detta “prodotto di solubilità” , simbolo Kps
Esempio per la soluzione in acqua del solfato di Ba
BaSO4(s) ÅÆ Ba2+(aq)+ SO42-(aq) Kps= [Ba2+(aq)][SO42-(aq)] = 1.0x10-10
Problema 1
Dato il prodotto di solubilita’ Kps = 1.x10-10 ,calcolare la solubilita’ in acqua del solfato di Ba espressa in
g/L.
Dalla stechiometria della dissociazione si ha: [Ba2+(aq)] = [SO42-(aq)]
sostituendo si ha: Kps = [Ba2+(aq)]2= 1x10-10, [Ba2+(aq)]= 10-5 M
dalla stechiometria : [Ba2+(aq)] = CBaSO4 = 10-5 M
P.F ( BaSO4) = 233.3 ; mole = 233.3 g/mole
Solubilita’ di BaSO4 = 233.3 x 10-5 = 0.0233 g/L
Problema 2
Il prodotto di solubilita’ di CaF2 e’ Kps = 3.4x10-11 : calcolare la solubilita’di questo sale espressa in g/L
Equilibrio di solubilita’: CaF2 ÅÆ Ca2+(aq) + 2 F-(aq)
Kps= [Ca2+(aq)][F-(aq)]2 = 3.4x10-11
dalla stechiometria: [F-(aq)] = 2[Ca2+(aq)]; Kps= [Ca2+(aq)] x (2[Ca2+(aq)])2 = 3.4x10-11
[Ca2+(aq)] = ( 3.4x10-11/4)1/3 = 2.04x10-4 M
P.F ( CaF2) = 78; mole = 78 g/mole
Solubilita’ di CaF2 = 78 x 2.04x10-4 = 1.59x10-2 (g/L)
-----------------------------------------------------------------------------------------------------------------------------------
Prodotto di solubilita’
Un solido si scioglie in un liquido sino a raggiungere una concentrazione massima detta di saturazione.
Questa concentrazione limite e’ la conseguenza di un equilibrio dinamico fra il solido presente come corpo
di fondo e le sue particelle costitutive ( ioni, molecole) in soluzione. La costante di questo equilibrio e’
convenzionalmente detta “prodotto di solubilità” , simbolo Kps
Esempio per la soluzione in acqua del solfato di Ba
BaSO4(s) ÅÆ Ba2+(aq)+ SO42-(aq) Kps= [Ba2+(aq)][SO42-(aq)] = 1.0x10-10
7
Problema 1
Dato il prodotto di solubilita’ Kps = 1.x10-10 ,calcolare la solubilita’ in acqua del solfato di Ba espressa in
g/L.
Dalla stechiometria della dissociazione si ha: [Ba2+(aq)] = [SO42-(aq)]
sostituendo si ha: Kps = [Ba2+(aq)]2= 1x10-10, [Ba2+(aq)]= 10-5 M
dalla stechiometria : [Ba2+(aq)] = CBaSO4 = 10-5 M
P.F ( BaSO4) = 233.3 ; mole = 233.3 g/mole
Solubilita’ di BaSO4 = 233.3 x 10-5 = 0.0233 g/L
Problema 2
Calcolare la solubilita’ di BaSO4 in una soluzione acquosa contenente 0.05 moli/L di Na2SO4
Na2SO4 Æ 2 Na+ + SO42- , percio’ 0.05 moli/L di Na2SO4 = 0.05 moli/L di SO42Dalla relazione Kps= [Ba2+(aq)][SO42-(aq)] = 1.0x10-10 con [SO42-(aq)] = 0.05 M si ottiene:
[Ba2+(aq)] = 1.0x10-10/ 0.05 = 2.0x10-9 M ;
solubilita’ di BaSO4= 2.0x10-9 x233.3= 4.66x10-7 M
Problema 3
Il prodotto di solubilita’ di CaF2 e’ Kps = 3.4x10-11 : calcolare la solubilita’di questo sale espressa in g/L
Equilibrio di solubilita’: CaF2 ÅÆ Ca2+(aq) + 2 F-(aq)
Kps= [Ca2+(aq)][F-(aq)]2 = 3.4x10-11
dalla stechiometria: [F-(aq)] = 2[Ca2+(aq)]; Kps= [Ca2+(aq)] x (2[Ca2+(aq)])2 = 3.4x10-11
[Ca2+(aq)] = ( 3.4x10-11/4)1/3 = 2.04x10-4 M
P.F ( CaF2) = 78; mole = 78 g/mole
Solubilita’ di CaF2 = 78 x 2.04x10-4 = 1.59x10-2 (g/L)
--------------------------------------------------------------------------------------
8
EQUILIBRI DI FASE
Calcoli numerici con l’equazione di Clapeyron sugli equilibri liquido-vapore e solido-vapore.
Problema 1
la pressione di vapore di un liquido e’ pari a 1.5 atm a 100 °C e 2.5 atm a 200 °C: calcolare
l’entalpia di evaporazione ΔHev
P1 = 1.15 atm , T1 = 373.1 K; P2 = 2.5 atm, T2 = 473.1 K
P2 ΔH v ⎡ 1 1 ⎤
R = 8.314 (jxmole-1K-1)
=
⎢ − ⎥
P1
R ⎣ T1 T2 ⎦
Risolvendo rispetto a ΔHv :
ΔHv = 7496.4 (J)
Equazione di Clapeyron: ln
Problema 2
L’acqua bolle a 100 °C alla pressione di una atmosfera e ha un’entalpia di evaporazione ΔHev pari a
10.5 kcal/mole: calcolare la pressione di vapore a 150 °C
P1=1 atm, T1 = 373.1 K; P2 = ?, T2 = 423.1 K R = 1.986 cal x mole-1x K-1
Risolvendo l’equazione di Clapeyron rispetto a P2 : P2 = 5.33 atm
9
TERMODINAMICA
Definizioni
U, energia interna del sistema
H = U + PV , entalpia del sistema
S = entropia del sistema
G = H-TS, energia libera del sistema
ΔU variazione di energia interna associata alla reazione, passaggio di stato, etc
ΔH, variazione di entalpia associata alla reazione, passaggio di stato, etc
A pressione costante, ΔH = ΔU + PΔV
PΔV = lavoro meccanico di espansione o compressione dei gas a P costante
ΔH = Qp , calore di reazione a P costante ( solo lavoro PV)
ΔH<0, reazione esotermica, avviene con sviluppo di calore; ΔH>0, reazione endotermica, avviene
con assorbimento di calore
ΔH° ,entalpia standard di reazione: i reagenti e i prodotti sono nello stato standard.
Per ogni sostanza lo stato standard e’, di norma, lo stato fisico stabile a T = 25 ° e P = 1 atm (si
assume comportamento ideale per i gas). Per ioni e molecole in soluzione, lo stato standard e’
riferito alle soluzioni ideali con concentrazioni molari unitarie
ΔHf°, entalpia di formazione standard di un composto: e’ l’entalpia della reazione di formazione di
una mole di composto a partire dagli elementi nello stato standard. Per esempio, i ΔHf° di CH4,
CO2, H2O sono associati alle reazioni:
C(s) + 2 H2 (g) Æ CH4(g) , ΔHf° (CH4) = -17.89 kcal/mole
C(s) + O2 (g) Æ CO2(g) , ΔHf° (CO2) = -94.05kcal/mole
H2(g) + ½ O2 (g) Æ H2O(l), ΔHf° (H2O) = -68.3 kcal/mole
Per le reazioni in soluzione, i ΔHf° degli ioni si calcolano dalle ossidoriduzioni ottenute
accoppiando le semireazioni di ossidazione dagli elementi con la semireazione di riduzione dello
ione idronio H+(aq)
Esempio:
per lo ione Zn2+(aq) : Zn(s) + 2H+(aq) Æ Zn2+(aq) + H2(g) ΔHf°(Zn2+(aq)) = -152.5 kJ/mole
Cu(s) + 2H+(aq) Æ Cu2+(aq)+ H2(g) ΔHf°( Cu2+(aq)) = 64.4 kJ/mole
per lo ione Cu2+(aq)
Per definizione le sostanze elementari hanno ΔHf° = 0; inoltre, per le reazioni in soluzione,
ΔH°f (H+) = 0.
I ΔHf° si determinano sperimentalmente e sono disponibili in apposite banche dati.
I ΔH° delle reazioni si calcolano dalla differenza tra i ΔHf° dei prodotti e i ΔHf°dei reagenti.
p
R
i =1
j =1
ΔH ° = ∑ ΔH fi ° − ∑ ΔH fj °
i,j indici per prodotti e reagenti rispettivamente
ENTROPIA S
ΔS°= Qrev/T; S = k lnW k = R/Nav (costante di Boltzmann); W = probabilita’ di stato;
l’entropia e’ una misura del grado di disordine del sistema: aumenta nei passaggi di stato solidoÆ
liquidoÆ vapore, nell’espansione di un gas, all’aumentare del numero di moli in una reazione.
ΔS° di una reazione = differenza tra l’entropia totale dei prodotti e l’entropia totale dei reagenti
nello stato standard:
p
R
i =1
j =1
ΔS ° = ∑ S fi ° − ∑ S fj °
I valori di S° sono determinati sperimentalmente e disponibili in apposite banche dati. I valori
assoluti della funzione termodinamica sono in questo caso attingibili per effetto del 3° principio di
termodinamica che pone = zero l’entropia di un solido nello stato cristallino perfetto a 0 K
ENERGIA LIBERA. G
Definizione
G = H- TS
10
Per le reazioni e processi in genere:
ΔG° = ΔH°-TΔS°
ΔG corrisponde al lavoro utile massimo ottenibile in un processo reversibile
Isoterma di reazione:
ΔG = ΔG° + RT lnQ
ΔG e’la variazione istantanea dell’energia libera rapportata al procedere della reazione (e’ in
sostanza la derivata dell’energia libera rispetto alla coordinata di reazione); Q = quoziente di
reazione; il quoziente di reazione ha la stessa forma della costante di equilibrio ma, a differenza di
questa, e’ variabile, cresce con il procedere della reazione e coincide con K solo all’equilibrio.
All’equilibrio il sistema si trova al minimo di energia libera e pertanto ΔG = 0
sostituendo ΔG = 0 e Q = K nell’isoterma : ΔG° = - RT ln K ; K = exp(-ΔG°/RT)
ΔG° e’ pertanto la funzione termodinamica dalla quale si calcola la costante di equilibrio che a sua
volta si impiega per il calcolo delle rese dei prodotti
Esempio di isoterma di reazione: per la reazione N2(g) + 3H2(g) ÅÆ 2 NH3(g)
ΔG = ΔG° + RT ln [P2NH3/( PN2 xPH23)];
all’equilibrio, ΔG° = - RT lnKp Kp = [P2NH3/( PN2 xPH23)]
Criterio di spontaneita’ delle reazioni: la reazione e’ spontanea se ΔG < 0.
La reazione procede spontaneamente nella direzione in cui si ha diminuzione dell’energia libera del
sistema; pertanto la derivata dell’energia libera rispetto alla coordinata di reazione (ovvero ΔG) e’
negativa .
Poiche’ ΔG = ΔH-TΔS, la spontaneita’ della reazione sara’ determinata dal segno e dal modulo del
termine entalpico (ΔH) e del termine antropico (TΔS)
Effetto della temperatura sulla costante di equilibrio: Equazione di vant’Hoff
ΔH ° ΔS °
ln K = −
+
RT
R
Si considerano approssimativamente costanti ΔH° e ΔS°
La temperatura alla quale K = 1 si ottiene dalla relazione:TK=1 = ΔH°/ΔS°
Problema 1
Data la reazione di combustione: CH4(g) + 2 O2(g) Æ CO2(g) + 2 H2O(l),
usando i dati dei ΔHf° sopra riportati, calcolare il calore sviluppato a P costante dalla reazione di 1.5
m3 di CH4 (volume misurato a P = 200 atm e T = 25 °C )
Calcolo del ΔH°
ΔH° = 2xΔHf° (H2O) +ΔHf° (CO2) - ΔHf° (CH4) = 2(-68.3) + (-94.05) - (-17.89) = -212.76
La combustione di 1 mole di CH4 sviluppa 212.76 kcal
Calcolo del numero di moli di metano nel volume dato:
n = PV/RT , P= 200 atm, T = 298.1 K, R = 0.0821 L atm mole-1K-1, V = 1.5x103 L,
n= 12257.9 moli
Qp = n x ΔH° = 212.76 x 12257.9 = 2.61x106 kcal
Problema 2
Data la reazione endotermica di reforming del metano usata per produrre idrogeno:
CH4(g) + H2O(g) Æ CO(g) + 3 H2(g),
quanto calore assorbe la reazione per produrre 10 m3 di H2 (misurati a P = 1tm e T = 25°)
Dati: ΔHf° (CH4) = -17.89 kcal/mole; ΔHf° (H2O(g)) = -57.8 kcal/mole; ΔHf° (CO) = -26.4
kcal/mole
N.B. il ΔHf° (H2O(g)) e’< ΔHf° (H2O(l)); la differenza corrisponde al calore molare di evaporazione
H2O(l) Æ H2O (g) ΔHevap° = 10.5 kcal/mole
Calcolo del ΔH°:
ΔH° = ΔHf°(CO) -ΔHf°( H2O) -ΔHf°(CH4) = -26.4 - ( -17.89) – (-57.8) = 49.33 kcal
Occorrono 49.33 kcal per produrre 3 moli di H2
11
Calcolo delle m oli di H2 nel volume dato:
n = PV/RT , P= 1 atm, T = 298.1 K, R = 0.0821 L atm mole-1K-1, V = 1.0x104 L, n = 408.59
moli
Qp = 408.59 x 49.33 = 20156 kcal
Problema 3
Data la reazione C(s) +H2O(g)Æ CO(g) + H2(g)
-Calcolare ΔH°, ΔS°, ΔG° e la Kp a 298 K, la T alla quale Kp = 10
-Date le condizioni iniziali: moli di C = 1; moli di H2O = 1 , P = 1 atm , calcolare la resa di
formazione di H2 rispetto a H2O ( si assuma Kp = 1)
Dalla tabella:
S°(kj/mole/K)
ΔHf°(kj/mole
C(s)
0.
0.0057
H2O(g)
-241.8
0.1887
CO(g)
-110.5
0.198
H2(g)
0.
0.1306
ΔH° = ΔHf°(CO) -ΔHf°(H2O(g)) = -111.0 – ( -242.0) = 131.3 (kJ)
ΔS° = S°(CO) +S°(H2) – S°(H2O(g)) – S°(C) = 0.134 (kJ/K)
ΔG°= ΔH° -TΔS° = 91.37 ( kJ)
LnKp= -ΔG°/RT = -91.37/(8.314x10-3 x298)= -36.88 Kp = 9.63x10-17
Kp = 1 per T = ΔH°/ΔS°= 131.3/0.134 = 979.8 K ( 706.8 °C)
Calcolo della resa:
Reagenti e prodotti
C(s)
H2O(g)
CO(g)
H2(g)
Inizio reazione
All’equilibrio
1-y moli
1-y moli
Y moli
Y moli
Moli totali Æ 1+ y
NB si considerano solo I prodotti e reagenti gassosi
1 mole
1 mole
0
0
Si calcolano le frazioni molari e le pressioni parziali (legge di Dalton):
XH2O = (1-y)/(1+y); XCO = y/(1+y); X(H2) = y/(1+y)
PH2O = (1-y)/(1+y)P ; PCO= y/(1+y)P ; PH2= y/(1+y)P
Sotituendo nell’equazione della Kp : Kp = (y2)P2/[(1+y)(1-y)P]
Risolvendo rispetto a y: y = ± [(Kp/(P+Kp)]1/2
Ponendo Kp = 1 e P = 10 atm, y = ±0.301
Si scarta la soluzione negativa ( non ha significato fisico): y = 0.301
Resa percentuale rispetto al reagente H2O : R = (moli reagite/moli iniziali)x100 = 30.1 %
N.B con P = 1 atm, R = 70.7% l’aumento della pressione sfavorisce la reazione perche’ Δn >1
Problema 4
Data la reazione Cu2+(aq) + Zn(s) ÅÆ Cu(s) + Zn2+(aq)
Calcolare ΔH°, ΔS°, ΔG° e Kc a 25 °C
S° ( kJ mole-1K-1
ΔH°f (kJ/mole)
Cu2+(aq)
+ 64.4
-0.0987
2+
Zn (aq)
-152.5
-0.1046
Zn(s)
0.0
0.0414
Cu(s)
0.0
0.0333
12
ΔH° = ΔH°f(Zn2+(aq)) - ΔH°f(Cu2+(aq)) = -216.9 kJ
ΔS° = S°(Zn2+(aq)) + S°( Zn(s)) - S°(Cu2+(aq))-S°( Cu(s)) = -1.4x10-2 kJ K-1
ΔG°= ΔH° -TΔS° = -216.9 - (- 298.1x 1.4x10-2) = -212.73 kJ
Kc = exp(-ΔG°/RT) = exp( -( -212.73/(298x8.314-3))) = 1.94x1037
------------------------------------------------------------------------------------------------------------------------
13
ELETTROCHIMICA
Reazioni di ossidoriduzione, semireazioni, calcolo dei potenziali standard; calcolo dei
potenziali in condizioni non standard (applicazione dell’equazione di Nernst).
Data un’ossidoriduzione, le semireazioni di ossidazione e di riduzione si possono trovare con i relativi
potenziali nella tabella dei potenziali elettrochimici standard. In questa tabella tutte le semireazioni sono
orientate per convenzione nel senso della riduzione; di conseguenza per la semireazione di ossidazione il
segno del potenziale deve essere invertito
Problema 1
Data la reazione non bilanciata
MnO4- + H+ + Fe2+Æ Mn2+ + Fe3+ + H2O
Bilanciarla con le semireazioni, calcolarne il potenziale standard E° , il potenziale a pH = 2.5 ( si
assumano = 1 M le concentrazioni delle altre specie ioniche) e la cotante di equilibrio della reazione
Nella tabella si trova:
MnO4- + 8H++ 5 e- Æ Mn2+ +4 H2O E° = 1.49 V
Fe3+ + e- Æ Fe2+
E° = 0.77 V
Dal confronto con la reazione completa si vede che la seconda semireazione deve essere invertita
(orientata nel senso dell’ossidazione). Inoltre deve essere moltiplicata per 5 allo scopo di bilanciare gli
elettroni. Sommando infine membro a membro le due semireazioni (come se fossero equazioni algebriche) si
ottieniene la reazione completa bilanciata insieme al suo potenziale standard:
MnO4- + 8H++ 5 e- Æ Mn2+ +4 H2O
E° = 1.49 V
5 Fe2+ + 5 e- Æ 5 Fe3+
E° = - 0.77 V
------------------------------------------------------------------------------Reazione bilanciata MnO4- + 8 H+ + 5Fe2+Æ Mn2+ + 5Fe3+ + 4H2O E° = 1.49 + ( - 0.77) = 0.72 V
N.B. la moltiplicazione x5 della semireazione di ossidazione non modifica il valore del suo potenziale.
Infatti E° e’ una proprieta’ intensiva che dipende dalla concentrazione e non dal n° di moli delle specie
attive nelle semireazioni
Calcolo del potenziale a pH 2.5: si usa l’equazione di Nernst:
[
][
5
]
8.314 x 298
Fe 3+ Mn 2+
E = 0.72 −
ln
8
−
5 x96490
MnO4 H + Fe 2+
a PH=2.5, [H+] = 10-pH = 3.16x10-3
[
][ ] [
]
5
E = 0.72 – 0.00513 ln 1020 E = 0.72- 0.236 = 0.483 V
NB nelle condizioni standard, [H+] = 1M ( soluzione ideale) e pH = 0. Pertanto il risultato dimostra che
l’aumento del pH sfavorisce la reazione.
Corrosione dei metalli
La corrosione dei metalli e’ sostanzialmente un’ossidazione che avviene in presenza di O2 e H2O. Si
puo’ rappresentare con due tipi di reazioni ( riferite al Fe a titolo di esempio):
Fe + ½ O2 +2 H+ =Fe2+ + H2O
Fe + ½ O2 +H2O =Fe2+ + OHLe condizioni standard sono (soluzioni e gas ideali):
per la prima reazione:
[H+] =1 M ( pH = 0.), [Fe2+]=1 M,,PO2 = 1atm
per la seconda reazione: [OH-] =1 M ( pH = 14.), [Fe2+]=1 M,,PO2 = 1atm
La tendenza del metallo alla corrosione cresce con il potenziale di queste reazioni
Problema 1
- Scrivere le reazioni di corrosione del Fe e del Cu in ambiente acido, calcolare i potenziali
standard, confrontare le relative tendenze alla ossidazione.
Fe + ½ O2 +2 H+ =Fe2+ + H2O
Dall tabella:
Semireazione di riduzione :½ O2 + 2H+ + 2 e- = H2O, E° = 1.23 V;
14
Semireazione di ossidazione : Fe = Fe2+ + 2 e- , E° = 0.41 V
Potenziale standard reazione E° = 1.23 + 0.41 = 1.64 V
Cu + ½ O2 +2 H+ = Cu2+ + H2O
Semireazione di riduzione :½ O2 + 2H+ + 2 e- = H2O, E° = 1.23 V;
Semireazione di ossidazione : Cu = Cu2+ + 2 e- , E° = - 0.34 V
Potenziale standard reazione E°= 1.23 + ( -0.34) = 0.89 V
La tendenza ad ossidarsi cresce con il potenziale della reazione, quindi il Fe si ossida piu’ facilmente.
Problema 2
Applicando l’equazione di Nernst, calcolare il potenziale della reazione di corrosione del Fe a
pH= 7 e a PO2 = 0.25 atm. Si considerino = 1M le concentrazioni delle altre specie. Inoltre si
commenti l’effetto del pH
Fe + ½ O2 +2 H+ ÅÆ Fe2+ + H2O
Dall tabella:
Semireazione di riduzione :½ O2 + 2H+ + 2 e- = H2O, E° = 1.23 V;
Semireazione di ossidazione : Fe = Fe2+ + 2 e- , E° = 0.41 V
Potenziale standard reazione E° = 1.23 + 0.41 = 1.64 V
Equazione di Nernst:
E = 1.64 −
[ ]
[ ]
RT
Fe 2+
ln
2
1/ 2
nF
H + xPO 2
Introducendo: R= 8.314 (J mole-1 K-1) ; T = 298.1 K; n = 2 ; F = 96490 C ; [H+] = 10-pH = 10-7 M ; PO2 =
0.25 atm
E = 1.64 – 0.423 = 1.22 V
La tendenza del metallo alla corrosione diminuisce con l’aumentare del pH
Corrosione e protezione galvanica, passivazione
Passivazione.
Metalli con elevato potenziale di ossidazione e quindi elevata tendenza alla corrosione sono in relta’
resistenti perche’ si passivano. La passivazione e’ conseguenza della formazione di uno strato sottile
trasparente di ossido, molto compatto e aderente alla superficie del metallo, che impedisce la diffusione
dell’ossigeno. Cr, Zn, Al, sono esempi di metalli resistenti alla corrosione grazie alla passivazione
Coppie galvaniche
Nel contatto tra due metalli diversi si crea una coppia galvanica (pila in cortocircuito) che favorisce la
corrosione del metallo avente il potenziale di ossidazione maggiore (potenziale di riduzione minore).
Per esempio, nella coppia Fe/Cu, il Cu favorisce la corrosione (ossidazione) del Fe:
Fe
=Fe2+ + 2 e- E° = 0.44 V
2+
Cu + 2 e = Cu
E° = 0.34 V
-----------------------------------------------------------------------------------------------------Fe + Cu2+ =Fe2+ + Cu
E° = 0.44 + 0.34 = 0.77 V
Protezione galvanica
Si puo’ realizzare una protezione galvanica contro la corrosione stabilendo il contatto elettrico tra la struttura
metallica da proteggere e un altro metallo che abbia un potenziale di ossidazione maggiore.
Esempio. Una struttura in Fe puo’ essere protetta creando una coppia galvanica con Mg
Mg
= Mg2+ + 2 e- E° = 2.37 V
2+
Fe + 2 e = Fe
E° = - 0.44 V
-----------------------------------------------------------Mg + Fe2+ = Mg2+ + Fe E° = 1. 93 V
Problema 3
Indicare quali tra i metalli di seguito elencati non sono adatti a proteggere dalla corrosione una
struttura in ferro con il meccanismo della coppia galvanica e spiegare il perche’:
Zn, Sn, Cu, Cr, Hg, Pb, Mn, Ni
15
Dalla tabella:
Fe
= Fe2+ + 2 e- E° = 0.44 V
Inoltre:
Zn
= Zn2+ + 2 e- E° = 0.76 V
Sn
= Sn2+ + 2 e- E° = -0.14 V
Cr
= Cr3+ + 2 e- E° = 0.74 V
Cu
= Cu2+ + 2 e- E° = - 0.34 V
Hg
= Hg2+ + 2 e- E° = - 0.85 V
Pb
= Pb2+ + 2 e- E° = 0.13 V
Mn
= Mn2+ + 2 e- E° = 1.18 V
Ni
= Ni2+ + 2 e- E° = 0.25 V
I metalli che hanno potenziali di ossidazione E° < 0.44 V , nella coppia galvanica con il Fe favoriscono la
sua ossidazione (corrosione). Pertanto Sn, Cu, Pb,, Ni non sono adatti a proteggere il Fe.
Tuttavia alcuni di questi metalli, per effetto della loro minore tendenza ad ossidarsi, possono esercitare un
effetto protettivo formando uno strato che ricopra omogeneamente la superficie del Fe; sono esempi la
banda stagnata (o latta) e le strutture in Fe annegate nel Pb ( tecnica usata dai Romani).
Pile e accumulatori
Possono essere oggetto di domanda nella prova in itinere l’accumulatore al Pb, le pile al Li/MnO2 e la cella a
combustibile H2/O2 (si veda il libro di testo, Silvestroni)
---------------------------------------------------------------------------------------------------------------------