Esercizi

Lente divergente Esercizio
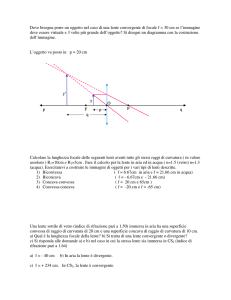
L’immagine prodotta da una lente divergente di lunghezza focale 25 cm, si trova nello spazio oggetto e dista 20 cm dal centro della lente. P = ? .
p
q=20
p
Lente convergente
f =25
con p > > f
( Obiettivo Microscopio composto)
Un oggetto alto 7.6 cm viene posto a 100 cm dalla lente di una macchina fotografica avente lunghezza focale +5 cm. Determinare posizione e dimensione dell'immagine prodotta dalla lente.
Per l'equazione p.c. lenti sottili
O
FF
p =1 m
I
f = 5 cm
q =?
.
Microscopio Semplice
p < f ( Lente ingrandimento)
Se p < f ( oggetto a p = +4 cm dalla lente f = 5 cm), posizione immagine e dimensione
hi
p=4
f=5
p
q
Esercizio -1
Una lente biconvessa con R1 = 10 cm e R2 = 20 cm ed n2 = 1,5
Calcolare la lunghezza focale quando è immersa in aria ( n1 = 1) e in acqua ( n1 = 1,33)
Esercizio 1
L’indice di rifrazione di un mezzo è n=1.36. La velocità della luce, in quel mezzo, vale quindi (c= 3
10 8 m/s). [220588 Km/s]
Esercizio 2
Se un’onda ha nel vuoto una lunghezza d’onda λ=589 nm, quanto vale la sua lunghezza d’onda nel
quarzo, sapendo che l’indice di rifrazione del quarzo è 1,458 ? [404 nm]
Esercizio3
A che distanza p da una lente convergente bisogna mettere l’oggetto affinché l’immagine nello spazio immagini sia un quarto dell’oggetto? La distanza focale della lente è 40 cm. [2m]
Esercizio 4
Un raggio luminoso di luce monocromatica incide sulla superficie di separazione tra aria (primo
mezzo) e acqua (secondo mezzo). Sapendo che l’angolo tra il raggio incidente e la superficie vale
48° e quello di rifrazione vale 40°, il rapporto tra l’indice di rifrazione dell’aria e quello dell’acqua
è:
Esercizio 5
Calcolare l’angolo limite per la rifrazione di un raggio luminoso proveniente da acqua ( n= 1,33) e
da glicerina (n=1,47).
Esercizio 6
Come deve essere la distanza p di un oggetto dalla lente sottile , affinché una lente convergente di
lunghezza focale f, fornisca una immagine virtuale, diritta e ingrandita?
Esercizio 7
Calcolare le diottrie delle seguenti lenti ( n =
n2
= 1,52 ):
n1
Biconcava: R1= 300 mm - R2= 300 mm +
Biconvessa: R1=400 mm + R2=250 mm Piano concava: R1=∞ R2=80 mm +
Esercizio 8
Un oggetto è posto a 12 cm da una lente divergente con f = - 8 cm. Trovare posizione, tipo e ingrandimento dell`immagine.
Esercizio 9
Un oggetto posto in acqua appare, visto dal di fuori, meno profondo di quanto non sia in realtà. Dove sembra essere una sorgente puntiforme di luce, posta sul fondo di una piscina piena d'acqua, profonda 2 m ?
(naria = 1; nacqua = 1.33)
Esercizio 10
Dato un diottro sferico convesso, indicando con n1 ed n2 gli indici di rifrazione rispettivamente del
primo mezzo e del secondo, con n1 > n2, l’immagine di un punto posto sull’asse ottico risulterà…
[sempre virtuale]
Esercizio 11
Un paziente ipermetrope ha il punto prossimo a 100 cm. Che potenza dovranno avere lenti dei suoi
occhiali per leggere il giornale a 25 cm dagli occhi? Le lenti sono indossate a 1 cm dagli occhi.
Esercizio 12
Calcolare la distanza focale di una lente necessaria alla visione vicina di un ipermetrope che mette a
fuoco per d > 50 cm.
Esercizio 13
Un miope ha il punto remoto a 17 cm (invece di infinito) e il punto prossimo a 12 cm ( invece di
25 cm). Quale deve essere la potenza della lente correttiva per vedere gli oggetti all’infinito ?
Distanza occhio –lente è 2 cm.
Quale deve essere la potenza della lente correttiva per vedere gli oggetti all’infinito ?
Con questi occhiali dove sarà il punto prossimo ?
Esercizio 14
Calcolare la distanza focale di una lente divergente che corregga una miopia per la quale l’occhio a
riposo non riesce a focalizzare oggetti a distanza superiore a 40 cm.
Esercizio 15
Una lente di ingrandimento ha lunghezza focale 8,0 cm. Stimare l'ingrandimento angolare con l'occhio rilassato cioè focalizzato all’infinito e con l'occhio focalizzato al suo punto prossimo 25 cm.
Esercizio 16
Calcolare il potere diottrico della Cornea ( R= 8mm n = 1,33) e del Cristallino ( R1=10mm; R2= 6
mm n’= 1,44)
Esercizio 17
Calcolare il potere diottrico dell’occhio normale rilassato n1= aria =1
p = ∞ d = 6,5 mm ( distanza cornea-cristallino)
n2= cornea+ u.vitreo=1,33
Esercizio 18
Quale deve essere la distanza focale di una lente che corregge una miopia di 2 diottrie?
Risp: 0.5 m
Esercizio 19
Quale deve essere la p di un oggetto affinché una lente sottile, convergente di lunghezza focale f,
fornisca una immagine virtuale, diritta e ingrandita? [p<f]
Esercizio 20
Un microscopio composto è costituito da un oculare 10x e da un obiettivo 50x posto a 17 cm Determinare l'ingrandimento totale, la lunghezza focale delle lenti, la posizione dell'oggetto in corrispondenza della quale l'immagine finale si trova a fuoco per l'occhio rilassato.( inf)
Esercizio 21 ( NO)
Immaginiamo di essere a L=10.000 m di altezza e di voler stimare la minima separazione s tra due
oggetti a terra che possa essere risolta a occhio nudo, considerando solo gli effetti della diffrazione,
La pupilla ha diametro di 3 mm e λ = 550 nm.
Esercizio 22 NO
Considerando due punti distino tra loro 0,5 mm. Determinare a quale distanza massima dall’occhio
è possibile distinguerli.
Esercizio 23 (NO)
Se la macchina fotografica montata su un satellite spia è in grado di fotografare i titoli di un giornale alti 3 cm a un'altitudine di 100 km. Suppondo che l’unico limite alla risoluzione sia quello dovuto
alla diffrazione c che λ = 550 nm. Determinate quale dovrebbe essere il diametro dell' obiettivo.
Esercizio 24 NO
Un piccolo oggetto e' posto a 9 cm da uno specchio sferico concavo di raggio di curvatura 12 cm.
Trovare la posizione, il tipo e l'ingrandimento dell'immagine.
[18 cm; reale; 2X; capovolta]
Esercizio 25 No
Il telescopio rifrattore più grande oggi esistente si trova in Wisconsin. L'obiettivo ha diametro di
102 cm e lunghezza focale di 19 m, l'oculare ha lunghezza focale di 10 cm.
Calcolare l'ingrandimento del telescopio e stimare la lunghezza del telescopio.
A, incide sullo specchio in B e giunge in E.