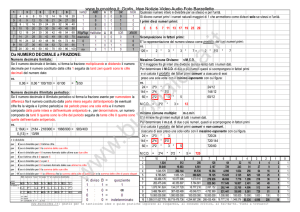
Conversione di decimali finiti dalla base 10 alla base 2
Giacomo CAPPELLARI
Si considerino i numeri decimali con la sola parte frazionaria.
Alcuni numeri si convertono in binario su un numero finito di bit (esempio 0.62510 = 0.1012), altri
su un numero infinito di bit (esempio 0.5310 = 0.10000111…2).
Ci si chiede a quali vincoli devono soddisfare i numeri decimali per essere convertiti su un numero
finito di bit.
Se un numero decimale frazionario si converte su un numero finito di bit, deve valere la relazione:
0.d1d2…dk = 0.b1b2…bh
Ovvero
d1d2…dk 10-k = b1b2…bh 2-h
Ora d1d2…dk sia D e b1b2…bh sia B
Si osservi che D non è divisibile per 10 e B non è divisibile per 2 (altrimenti i numeri non avrebbero
la forma data).
Uguagliando le due espressioni si ha:
D
B
h
k
10
2
10 k
2k
D B h B h 5 k B 2 k h 5 k
2
2
Per valori diversi di h e k succedono diverse cose:
kh
D B 10 k h 5 h
che è impossibile, poiché si è stabilito che D non deve essere divisibile per 10.
kh
D
B
2
hk
5k
anche questo è impossibile, perché per definizione B appartiene ai numeri naturali (e si è detto che
B non è divisibile per 2). Rimane soltanto un’opzione, ossia k h . In questo caso la formula
diventa:
D B 20 5k
D B 5k
Vale a dire, perché un decimale in base 10 possa essere tradotto in modo finito in base 2, è
necessario che sia un multiplo di 5, e precisamente che possa essere diviso per 5 elevato alla
potenza corrispondente al numero di cifre decimali di partenza. Queste cifre, inoltre, non variano in
numero nella traduzione da una base all’altra.
Nota: quest'ultima osservazione, facilmente verificabile (0.62510 = 0.1012, entrambi i numeri hanno
3 cifre nella parte frazionaria), non deve trarre in inganno: la precisione delle rappresentazioni non è
la stessa! La minima variazione percepibile nel numero decimale è 1/1000, mentre quella
percepibile nel numero binario è 1/8, e per avere la stessa precisione occorrerebbero 10 cifre nella
parte frazionaria del numero binario.