x - Scuole Toscane

A.A. 2007­2008
Università degli Studi di Firenze
SCUOLA DI SPECIALIZZAZIONE PER L’INSEGNAMENTO
SECONDARIO DELLA TOSCANA
Sede di Firenze
VIII ciclo
II anno
AREA DISCIPLINARE
MATEMATICA
UD REALE: TEORIA DELLE DERIVATE
Indirizzo : Specializzando:
Fisico – Matematico – Informatico
Tutor di aula:
Prof. Silla Maria Campion
1
Francesco Fontani
MODULO: DERIVATE E STUDI DI FUNZIONE
•
Teoria delle derivate
•
Teoremi del calcolo differenziale
•
Massimi, minimi e flessi
•
Lo studio delle funzioni
COLLOCAZIONE
classe 5° F, Liceo Scientifico ‘Russell-Newton’ di Scandicci. L’unità didattica
è stata affrontata nella seconda parte del primo quadrimestre e in parte
all'inizio del secondo, a cavallo tra Gennaio e Febbraio, dopo l’unità didattica
sulle funzioni continue.
PREREQUISITI
•
Rette nel piano cartesiano e significato geometrico di coefficiente
angolare;
•
Calcolo algebrico;
•
Rappresentazione
grafica
delle
funzioni
fondamentali
nel
cartesiano;
•
Limiti di funzioni e teoremi sui limiti;
•
Funzioni continue e punti di discontinuità;
•
Concetti fondamentali di cinematica del punto materiale.
OBIETTIVI COGNITIVI (SAPERE)
•
Conoscere la definizione di derivata di una funzione in un punto;
•
Conoscere e saper classificare i punti di non derivabilità;
•
Conoscere il legame tra continuità e derivabilità di una funzione;
•
Conoscere le derivate delle funzioni fondamentali;
•
Conoscere i teoremi sul calcolo delle derivate;
2
piano
•
Conoscere la definizione di velocità e accelerazione come derivata prima
e seconda della legge oraria.
OBIETTIVI OPERATIVI (SAPER FARE)
•
Saper applicare le regole di derivazione per calcolare derivate di
funzioni qualsiasi;
•
Saper capire l’andamento qualitativo della derivata di una funzione dal
suo grafico;
•
Saper riconoscere i punti di non derivabilità;
•
Saper trovare l’equazione della retta tangente ad una funzione in un
punto utilizzando la derivata;
•
Saper usare la derivata per risolvere problemi di fisica;
METODOLOGIA
L’unità didattica è stata svolta prevalentemente mediante lezioni frontali alla
lavagna e lezioni interattive in cui ho fatto svolgere ai ragazzi esempi ed
esercizi. Ho usato il libro di testo come traccia, anche se spesso sono andato
‘a braccio’ e non sempre ho seguito l'ordine degli argomenti presentati, e per
questo ho chiesto ai ragazzi di prendere appunti sul loro quaderno.
Ogni volta che ho spiegato un concetto nuovo, un nuovo teorema o una nuova
regola, alla lezione frontale ho fatto seguire esempi e/o esercizi alla lavagna.
Sono stati assegnati numerosi esercizi per casa analoghi a quelli fatti in
classe. Gli esercizi che hanno creato maggiori problemi sono sempre stati
corretti all’inizio della lezione successiva dai ragazzi stessi con il mio aiuto.
STRUMENTI
•
Lavagna, gessi colorati
•
Libro di testo
3
TEMPI E CONTENUTI
LEZIONI
DURATA
CONTENUTO
Lezione 1
1 ora
Definizione di derivata
Lezione 2
1 ora
Derivata destra e sinistra. Equazione della retta tangente
Lezione 3
1 ora
Punti di non derivabilità
Lezione 4
1 ora
Relazione tra continuità e derivabilità
Lezione 5
2 ore
Derivate di alcune funzioni fondamentali
Lezione 6
1 ora
Derivata di somma e prodotto di funzioni derivabili
Lezione 7
1 ora
Derivata del quoziente
Lezione 8
1 ora
Derivata della funzione composta
Lezione 9
1 ora
Esercizi sulla derivata di una funzione composta e verifiche orali
Lezione 10
1 ora
Derivata della funzione inversa
Lezione 11
1 ora
Significato fisico di derivata
Lezione 12
2 ore
Verifica sommativa
Lezione 13
1 ora
Correzione della verifica formativa e recupero
TOT: 15 ore
4
VERIFICHE
È stata fatta una verifica sommativa di due ore al termine dell'unità didattica.
Sono anche state fatte verifiche orali in itinere.
RECUPERO
Per tutti, sono stati usati 50 minuti per correggere alla lavagna la verifica
sommativa. Verrà poi organizzato un recupero pomeridiano solo per gli
studenti che hanno evidenziato particolari difficoltà.
PRIMA LEZIONE: DEFINIZIONE DI DERIVATA
INTRODUZIONE
Per introdurre l’argomento, ho cominciato la lezione mettendo in evidenza
che le derivate saranno uno strumento fondamentale soprattutto per
disegnare il grafico delle funzioni.
Ho fatto notare che, con gli strumenti che avevano al momento (vale a dire
studio del dominio e del segno, intersezione con gli assi e asintoti), si riesce a
capire in che parte del piano cartesiano sta la funzione, come si comporta
vicino agli assi e agli estremi del campo di esistenza, ma in generale non si sa
determinare il suo andamento locale.
Ho anche aggiunto qualche brevissimo cenno storico, dicendo che il calcolo
delle derivate risale al ‘600, quando Newton e Leibniz, indipendentemente
l’uno dall’altro, ne gettarono le basi teoriche partendo dal problema di trovare
l’equazione della retta tangente ad una curva qualsiasi.
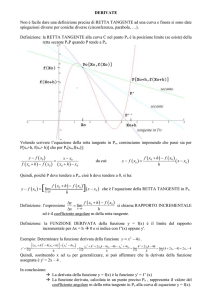
BREVE RICHIAMO SUL COEFFICIENTE ANGOLARE
Anche se questo è stato assunto come prerequisito, per essere sicuro di poter
partire senza problemi ho fatto un breve ripasso sul significato del coefficiente
angolare di una retta. In particolare, ho richiamato ai ragazzi che una retta di
coefficiente angolare m e passante per il punto P0(x0,y0), ha equazione:
y−y 0=m⋅ x−x 0
5
da cui segue immediatamente che, per qualsiasi punto P di coordinate (x,y), il
coefficiente angolare m rappresenta il rapporto tra la variazione della y, (y –
y0) e la variazione della x, (x –x0), nel passare dal punto P0 al punto P. In
particolare, se prendiamo su rette diverse la stessa variazione della x, per
semplicità prendiamo Δx = 1, la variazione della y sarà sempre
 y=m⋅1=m .
Pertanto, le rette con m maggiore variano più rapidamente la loro ordinata
per una stessa variazione dell'ascissa.
Ho poi chiesto ai ragazzi vari esempi di rette in cui m è positivo, negativo o
nullo, e ho anche ricordato il significato goniometrico del coefficiente
angolare: m rappresenta la tangente goniometrica dell’angolo che la retta
forma con l’asse delle x.
6
Definire un coefficiente angolare per una funzione qualsiasi non è possibile,
perché una funzione in generale non ha sempre la stessa variazione della y per
una uguale variazione della x: in generale, il rapporto tra la variazione della y e
della x su una funzione qualsiasi non dipende solo dalla ‘distanza’ tra le
ascisse, ma dipende anche dalla particolare coppia di punti che considero.
IL RAPPORTO INCREMENTALE
Sia data una funzione f(x) definita su ℝ o su un intervallo aperto di ℝ. Siano x0 e
x = x0 + h due punti del dominio della funzione, che supponiamo definita anche
in tutti i punti interni all’intervallo da essi individuato (vedi Fig. 1). La differenza
 x=x −x 0= x 0h−x 0=h
si dice incremento della variabile indipendente x al passaggio dal valore x0
a x = x0 + h. Poiché le due ascisse fanno parte del dominio della funzione, ad
esse corrispondono due punti sulla funzione P e Q di coordinate: P(x0, f(x0)) e
Q(x0 + h, f(x0 + h)).
Allora possiamo definire la differenza
 y= f  x 0h− f  x 0
si dice incremento della variabile dipendente y o della funzione f relativo
all’incremento h nel punto x0.
Definizione
Il rapporto tra l’incremento della variabile dipendente, f(x0 + h) – f(x0), e
l’incremento h della variabile indipendente si dice rapporto incrementale
della funzione f relativo al punto x0 e all’incremento h.
∆y f ( x 0 + h ) − f ( x 0 )
=
∆x
h
7
Figura 1: Il rapporto incrementale
Tracciando la retta s passante per i punti P e Q, come quella rappresentata in
Fig. 1, risulta evidente che cosa rappresenta geometricamente il rapporto
incrementale:
Fissato x0 , il rapporto incrementale della funzione f relativo all’incremento h
rappresenta il coefficiente angolare della retta passante per i punti P(x0 , f(x0))
e Q(x0 + h, f(x0 +h)).
8
LA DERIVATA DI UNA FUNZIONE
Nel grafico di Fig. 2 disegniamo adesso anche la retta t tangente al grafico
della funzione nel punto P.
Figura 2: La derivata di una funzione
Parentesi
A questo punto, ho chiesto ai ragazzi se sapevano la definizione di retta tangente ad una
curva, ed ho subito evidenziato un pò di confusione. Molti mi hanno detto che è una retta che
ha in comune con la curva un solo punto. Perciò è stato necessario anche definire il significato
di tangente ad una curva come la posizione limite della retta secante che passa per due punti
della curva, quando i due punti tendono a coincidere.
9
Dalla Fig. 2, si osserva che per valori di h sempre più piccoli, sia Δx che Δy
tendono a zero, e il punto Q si avvicina sempre più al punto P. Al limite per
h→0, Q tende a coincidere con P, e la retta secante s tende a sovrapporsi alla
tangente t. Ma allora, al limite per h→0, il coefficiente angolare della retta
secante s, che avevamo genericamente indicato con α in Fig. 1, tende a
diventare quello della tangente t, indicato con β in Fig. 2.
Definizione
Una funzione si dice derivabile nel punto x0 se esiste ed è finito il seguente
limite:
m = lim h →0
f ( x0 + h ) − f ( x0 )
.
h
Il numero m rappresenta geometricamente il coefficiente angolare della retta
tangente al grafico della funzione nel punto x0.
Il valore di tale limite viene chiamato derivata della funzione f nel punto
x0 e viene indicata con uno dei seguenti simboli:
f ' ( x0 ) (notazione di Lagrange)
D[ f  x] xo (notazione di Cauchy)
df
dx xo
(notazione di Leibnitz)
ḟ  x 0  (notazione di Newton)
Noi utilizzeremo soltanto le prime due, in particolare la prima.
Dalla definizione, segue immediatamente che, affinché una funzione y=f(x)
sia derivabile in un punto x0 , devono essere verificate queste 3 condizioni:
1. la funzione sia definita in un intorno del punto x0 ;
2. per h→0, deve esistere da destra e da sinistra il limite del rapporto
incrementale, ed essere un numero finito;
3. tali limiti destro e sinistro devono essere uguali.
10
Ho terminato la lezione con un esempio molto semplice di calcolo del limite
del rapporto incrementale: ho preso in considerazione la funzione
f(x) = x3 + 2, ed ho calcolato la sua derivata nel punto x0 = 1.
lim
f 1h− f 1
h­>0
h
3
=lim
[1h 2 ]−3
h­>0
h
3
=lim
2
h 3h 3h
h­>0
h
2
=lim h 3h3  3
h­>0
Esercizi per casa:
Dopo aver determinato il rapporto incrementale, calcolare il valore della
derivata delle seguenti funzioni nel punto x0 = 0.
1. y = −3x 2 + 2 x − 12
2. y =
x−3
1 − x2
SECONDA LEZIONE: FUNZIONE DERIVATA, DERIVATA DESTRA E SINISTRA E EQUAZIONE DELLA RETTA TANGENTE
FUNZIONE DERIVATA
La definizione di derivata è relativa ad un punto di ascissa x0. Tuttavia, si può
calcolare la derivata di una funzione anche in un punto qualsiasi, di ascissa x.
In questo modo, il limite del rapporto incrementale, che per un certo x0 è un
numero, diventa una funzione di x. Tale funzione viene detta funzione
derivata, e si indica con y ' = f ' ( x ) .
La lezione è proseguita con la correzione alla lavagna degli esercizi per casa,
rivolti al calcolo del limite del rapporto incrementale.
DERIVATA DESTRA E SINISTRA
11
Sono rispettivamente il limite destro e sinistro del rapporto incrementale.
Dalla definizione di derivata si ha quindi che una funzione è derivabile in
x0 se la derivata destra e sinistra sono finite ed uguali tra loro. Ma
questo fatto discende direttamente dalla definizione di limite, perciò sono
andato abbastanza velocemente su questo punto.
I simboli che si usano per indicare la derivata destra e sinistra sono:
f ' ¿ = derivata destra;
f ' −¿ = derivata sinistra
L'EQUAZIONE DELLA RETTA TANGENTE
Poiché ho notato che i ragazzi avevano chiaro il significato geometrico di
derivata, ho pensato di introdurre alcuni esercizi sull'equazione della retta
tangente al grafico di una funzione in un punto di ascissa data.
Per questo ho chiamato alla lavagna un alunno e gli ho chiesto di pensare a
y=x 2
come trovare l'equazione della retta tangente al grafico della funzione
nei punti di ascissa
x 0 =0 e x 0=1 , senza ricorrere ai metodi che avevano
usato in terza.
Con il mio aiuto, il ragazzo è arrivato alla soluzione dell'esercizio. Dopo di che,
visto l'esito un pò incerto, ho ritenuto opportuno spiegare il procedimento per
trovare l'equazione della retta tangente a una funzione in un punto generico:
consideriamo una funzione f(x) e un punto di ascissa
x0
appartenente al suo
dominio, e scriviamo la forma generica della retta che passa per il punto
 x0 ; y0 
come
y−y 0=m x −x 0  . Se
x0
è dato, ci mancano m e y0 .
y0 si ottiene semplicemente considerando che dovrà essere
essendo  x 0 ; y 0 
y 0= f  x 0 
perché,
il punto di tangenza, dal punto passa anche la funzione.
Per quanto riguarda m, la definizione di derivata implica che m= f '  x 0  .
12
Quindi, riepilogando, per ricavare l'equazione della retta tangente ad una
funzione, nota l'equazione della funzione e l'ascissa del punto di tangenza,
basta imporre le due condizioni:
•
m= f '  x 0 
•
y 0= f  x 0 
Esercizi per casa
Date le seguenti funzioni, trova la funzione derivata, e poi calcola l'equazione
della retta tangente al grafico della funzione nel punto P di ascissa x0 indicata
a fianco:
1. y=
x2
x 1
2. y=x 2 1
x0=0
x0=1
3. y= log 2x−1
x0=1
TERZA LEZIONE: PUNTI DI NON DERIVABILITÀ
Ho cominciato la lezione richiamando i concetti fatti nelle scorse lezioni, e
correggendo gli esercizi per casa.
Dopo di che, vedendo che i ragazzi avevano già chiaro il concetto di derivata,
ho affrontato il problema dei punti di non derivabilità, partendo da esempi.
13
Esempio 1: punti angolosi
Calcoliamo la derivata destra e sinistra della funzione y=∣x∣ in x0=0.
Il rapporto incrementale è
f  0h− f  0
h
=
∣h∣
h
. Il limite di tale rapporto è 1 per
h→0 da destra, mentre è -1 per h→0 da sinistra. Pertanto, nel punto x0=0 la
funzione non è derivabile perché non è soddisfatta l'ultima delle 3 condizioni
enunciate nella prima lezione (cioè i limiti destro e sinistro del rapporto
incrementale non sono uguali). Questo significa, geometricamente, che non è
possibile trovare nessuna retta tangente al grafico in quel punto. E questo
risulta evidente dal grafico della funzione nel punto x0=0:
I punti come questo, in cui la funzione non è derivabile perché le derivate
destra e sinistra esistono finite ma sono diverse, si dicono punti
angolosi.
y=|x|
Esempio 2: flessi a tangente verticale
Consideriamo la funzione y = 3 x e studiamo la sua derivabilità in x 0 = 0 .
Calcoliamo il rapporto incrementale nel punto in questione:
14
∆y f ( 0 + h ) − f ( 0 ) 3 h 3 h 3 h 2
h
1
=
=
=
⋅3
= 3
=3
∆x
h
h
h
h2 h h2
h2
Passando al limite otteniamo:
lim
h →0 ± 3
1
h2
= +∞
La funzione non è derivabile in zero perché la sua derivata nel punto è + ∞
quindi manca la seconda condizione (vale lo stesso risultato se il limite risulta
− ∞ ); tuttavia, la tangente al grafico in (0,0) esiste ed è una retta parallela
all’asse y, anzi in questo caso coincide esattamente con l’asse y perciò la sua
equazione è x = 0 . Anche se per le rette parallele all’asse y non è definito il
coefficiente angolare, si può dire in maniera un pò impropria che tali rette
hanno coefficiente angolare infinito.
In casi come questo in cui la derivata destra e sinistra sono uguali ma
infinite, se x0 è un punto interno all’intervallo in cui la funzione è definita,
diciamo che il punto (x0, f(x0)) è un punto di flesso a tangente verticale.
y=x^(1/3)
Esempio 3: cuspidi
15
Come ultimo esempio di punto di non derivabilità, consideriamo la funzione
3
y=  x−2 2 e calcoliamo il rapporto incrementale nel punto x0=2:

f  2h− f 2 
h
−∞
3
h
=
h
2
da cui risulta che il limite destro è ∞ e quello sinistro è
. La funzione non è derivabile in x0=2, e mancano sia il secondo che il
terzo requisito per la derivabilità, cioè i due limiti destro e sinistro del
rapporto incrementale sono diversi e infiniti. Punti di questo tipo si
dicono cuspidi.
y=((x­2)^2)^(1/3)
QUARTA LEZIONE: RELAZIONE TRA CONTINUITÀ E DERIVABILITÀ
Tutti gli esempi della lezione precedente hanno mostrato punti di non
derivabilità in cui tuttavia la funzione è continua. Questo risultato porta a
riflettere sul legame tra continuità e derivabilità delle funzioni.
16
Teorema
Se una funzione f(x) è derivabile in un punto x0 , in quel punto la funzione è
continua.
Dim.
Dobbiamo dimostrare che, se esiste finito lim
f  x 0h − f  x 0 
h ­> 0
h
= f '  x0 ,
lim f  x 0h= f  x 0  .
allora h ­> 0
Scriviamo f(x0 + h) in questo modo: f  x 0h= f  x 0
f  x 0h− f  x 0
h
⋅h , con h
diverso da 0;
calcoliamo il limite per h→0 di entrambi i membri della relazione precedente:
lim f  x 0h=lim f  x 0 lim
h­>0
h­>0
h­>0
f  x 0h − f  x 0 
⋅h .
h
Dei due limiti a secondo membro, il primo tende a f(x0), mentre il secondo,
sfruttando il teorema sul prodotto dei limiti e l'ipotesi fatta, tende a
f '  x 0 ⋅0=0 . Ora, poiché il limite della somma è la somma dei limiti, il limite a
secondo membro tende a f  x 0 0= f  x 0  . Ma allora, si ha che
lim f  x 0h= f  x 0  , cioè la fuzione è continua in x .
0
h­>0
Osservazione:
Il risultato inverso non vale, ovvero non è affatto detto che se una funzione è continua in un
punto allora nel punto è derivabile: tutti gli esempi fatti nella lezione precedente mostrano
funzioni non derivabili in punti in cui sono continue.
Ci sono dei casi in cui si è portati a pensare che il teorema non valga, cioè
funzioni con punti di discontinuità in cui si può erroneamente pensare che la
funzione sia derivabile. Mi sembra il caso di far riflettere i ragazzi su questo
per evitare problemi in futuro.
Esempio
17
Consideriamo la funzione y=
x 1 ; x≥0
x ; x 0
e discutiamo se x0=0 è un punto di
derivabilità.
Dato che y nel punto x0=0 ha un salto, è discontinua e quindi, per il teorema
appena enunciato, non derivabile. Tuttavia, si nota che le due leggi che
definiscono la funzione sono entrambe lineari, e il coefficiente angolare di
entrambe le rette è 1 (vedi grafico). Allora si può pensare che la derivata
destra e sinistra siano finite ed uguali, cioè che la funzione sia derivabile in
x0=0 sebbene nel punto non sia continua!
Ovviamente, si vede bene dal grafico che nel punto non è possibile definire
un'unica tangente.
Nel ragionamento che stiamo facendo, il 'baco' sta nel dire che la derivata
sinistra è 1, come quella destra. Infatti, se applichiamo la definizione di
derivata come limite del rapporto incrementale, da destra otteniamo:
lim
h­>0+
f 0h − f 0
h
=
h1−1
h
=1
18
mentre da sinistra si ha:
lim
f  0h− f 0 
h­>0­
h
=
h−1
h
=∞
Questo è un esempio che ha chiarito molto bene il significato di derivata a
tutti.
Esercizi per casa:
Date le seguenti funzioni, dimostra che non sono derivabili nel punto di
ascissa x0 indicata a fianco, indicando il tipo di non derivabilità:
1. y=∣x−3∣1 ; x 0 =3
2. y=
1
1−x 2
; x 0 =1
3
3. y= x 2 ; x 0=0
19
QUINTA LEZIONE: DERIVATE DI ALCUNE FUNZIONI FONDAMENTALI
Prima parte della lezione: correzione degli esercizi per casa, verifiche orali e
ripasso.
Seconda parte: a questo punto, ho ritenuto che i ragazzi fossero pronti per
introdurre le funzioni derivate delle funzioni fondamentali (che chiameremo
semplicemente derivate), che permettono di calcolare la derivata in ogni
punto senza dover ricorrere ogni volta al limite del rapporto incrementale.
Alcune sono state dimostrate, altre sono state date senza dimostrazione.
1. Derivata di una funzione costante
La derivata di una costante vale zero.
f ( x ) = k ⇒ f '( x ) = 0
Infatti:
k−k
= lim 0 = 0 .
h →0
h →0
h
f ' ( x ) = lim
Questo risultato ha un’interpretazione geometrica molto semplice: il grafico
della funzione y = k è una retta parallela all’asse x. La tangente a questo
grafico coincide evidentemente in ogni suo punto con questa retta e quindi
forma con l’asse x un angolo la cui tangente y' è uguale a zero.
2. Derivata della funzione identica
La derivata della funzione identica
y=x
vale 1.
f ( x ) = x ⇒ f '( x) = 1
Infatti:
f ' ( x ) = lim
h →0
( x + h ) − x = lim1 = 1
h
h →0
.
Anche questo risultato ammette una semplice interpretazione geometrica. Il
grafico della funzione y = x è la bisettrice del I e III quadrante. La tangente a
questo grafico è la bisettrice stessa, che ha coefficiente angolare 1.
3. Derivate delle funzioni sen(x) e cos(x)
20
Cominciamo con la derivata del seno:
f  x =sin  x  f '  x =cos  x 
Infatti:
lim
sin  xh−sin  x 
h
h­>0
..=sin  x ⋅lim
=lim
sin  x cos h cos  x sin  h−sin  x
h
h­>0
cos h −1
h­>0
h
cos  x ⋅lim
sin  h
h­>0
h
=..
.
Il secondo termine tende a cos(x), ricordando il limite notevole:
lim
h­>0
sin h
h
1 .
Operiamo ora sul primo termine: moltiplicando numeratore e denominatore
per cos h 1 e sfruttando il limite notevole precedente, si trova:
cos h−1
cos 2 h −1
−sin 2 h
−sin h  sin h 
lim
=lim
=lim
=lim
⋅
−1⋅0  0
h
h
cos h1
h­>0
h­>0 h cos h1
h­>0 h cos h1
h­>0
perciò la derivata della funzione sin(x) è cos(x).
La dimostrazione della derivata di cos(x) viene data per esercizio.
4. Derivata della funzione potenza
La derivata della potenza ad esponente reale è uguale al prodotto
dell’esponente per la base elevata all’esponente diminuito di 1.
f ( x ) = x α , α ∈ ℜ ⇒ f ' ( x ) = αx α−1
Questo risultato viene dato senza dimostrazione. In compenso, vale la pena
fare molti esempi:
Esempi
f ( x ) = x5
f ( x) =
1
x
f ( x) =
1
x4
f ( x) = x
→ f ' ( x ) = 5x 5 −1 = 5x 4
→ f ( x ) = x −1 → f ' ( x ) = −1x −1−1 = − x − 2 = −
→ f ( x ) = x −4
→ f ( x ) = x1 / 2
1
x2
→ f ' ( x ) = −4 x − 4 −1 = −4 x −5 = −
→ f '( x ) =
1
1
4
x5
1 2 −1 1 − 2 1 1
1
x = x =
=
1/ 2
2
2
2x
2 x
21
5. Derivata della funzione esponenziale e logaritmica
La derivata della funzione esponenziale a x è data dalla seguente espressione:
D[a x ]=a x log  a
mentre la derivata della funzione logaritmica log a  x  è data da:
1
D[ log a  x]= ⋅log a e .
x
Se ne deduce che le derivate di y=e x e y=ln  x  , cioè quando a=e, sono date
rispettivamente da:
x
D[e ]=e
x
D[ln  x ]=
1
x
Anche questi risultati sono stati dati senza dimostrazione, ma ho chiesto ai
ragazzi di studiare da soli la dimostrazione della derivata della funzione
esponeziale come compito a casa.
SESTA LEZIONE: DERIVATA DI SOMMA E PRODOTTO DI FUNZIONI
In questa lezione ho presentato i teoremi fondamentali sul calcolo delle
derivate. Anche in questo caso, alcuni teoremi vengono dimostrati mentre
altri vengono dati senza dimostrazione o lasciati per esercizio.
Teorema
La derivata della somma di due o più funzioni derivabili esiste ed è uguale
alla somma delle derivate di queste funzioni.
h( x ) = f ( x ) + g( x ) ⇒ h ' ( x ) = f ' ( x ) + g' ( x )
Dim.
h '  x =lim
[ f  xhg x h ]−[ f  x g  x ]
h­>0
..= f '  xg '  x 
h
=lim
[ f  x h − f  x][ g xh−g  x]
h­>0
h
poichè il limite della somma è la somma dei limiti.
Possiamo generalizzare al caso della somma di più funzioni.
22
=..
Esempi
1. D[32 x x 2 ]=02 x ln  22x
3 2
2 1
2. D[ cos  x  x ]=−sin  x ⋅ 3
3 x
23
Teorema
la derivata del prodotto di due funzioni è uguale al prodotto della derivata
della prima funzione per la seconda non derivata più la derivata della seconda
funzione per la prima non derivata.
h ( x ) = f ( x ) ⋅ g( x ) ⇒ h ' ( x ) = f ' ( x ) ⋅ g( x ) + f ( x ) ⋅ g ' ( x )
Dim.
Si ha:
D[h  x ]=lim
[ f  xh ⋅g  xh]− f  x ⋅g  x 
h
h­>0
da cui, aggiungendo e sottraendo f  xh⋅g x  , si ottiene:
lim
f  x h⋅g  xh− f  xh⋅g  x  f  xh⋅g x − f  x ⋅g  x 
h
h­>0
=..
g  xh−g  x 
f  xh− f  x 
lim f  xh⋅
lim g  x ⋅
 f  x ⋅g '  xg  x ⋅f '  x
h­>0
h
h­>0
h
Come per la somma, si può generalizzare al caso di più di due funzioni: si
procede analogamente derivando di volta in volta una funzione diversa e
mantenendo “fisse” le altre.
Osservazione 1: derivata del prodotto di f(x) per una costante
chiaramente nel caso particolare in cui f(x) è una costante,
applicando
il
teorema
precedente
si
ottiene
f  x =k ,
semplicemente:
D [ k⋅ f  x]=k⋅ f '  x 
Osservazione 2: derivata della potenza n-esima di f(x)
Come ulteriore applicazione della regola di derivazione del prodotto, si
osserva che si ha, per n ∈ N:
n
D[ f  x] =D[ f  x ⋅ f  x⋅f  x ... f  x ]= f '  x ⋅f  x ⋅...⋅ f  x f  x⋅f '  x ⋅f  x ⋅...⋅f  x ...
24
... f  x ⋅f  x ⋅...⋅f '  x =n [ f  x ]
n−1
⋅f '  x  .
La formula può essere generalizzata a un esponente qualsiasi.
Esempi
1. D [ x⋅sin  x ]=1⋅sin  x x⋅cos x 
x
x
x 1
2. D[e ⋅log 2  x]=e ⋅log 2  xe ⋅ log 2  e
x
1
3. D[ x⋅sin  x ⋅log3  x ]=1⋅sin  x ⋅log 3  x x⋅cos x ⋅log3  x x⋅sin  x ⋅ log 3 e
x
Esercizi per casa:
Calcolare la derivata delle seguenti funzioni:
x
1. 3 log 4  x
2
2. 25x 
3.
1
x
−7
3
 x ⋅cos  x sin  x−  x
4. x 3⋅e x 2 x
5.
1
⋅ln  x cos x ⋅  x
x2
6. sin 2  x⋅ln  x 
SETTIMA LEZIONE: DERIVATA DEL QUOZIENTE
Nella prima parte della della lezione abbiamo corretto gli esercizi per casa.
Nella seconda parte ho spiegato la derivata del quoziente di due funzioni:
Teorema
La derivata del quoziente di due funzioni è una frazione in cui a denominatore
abbiamo il denominatore della funzione di partenza al quadrato e a
numeratore la differenza tra la derivata del numeratore per il denominatore
non derivato e il numeratore non derivato per la derivata del denominatore.
h( x ) =
f ( x)
g( x )
⇒ h' ( x ) =
f ' ( x ) ⋅ g( x ) − f ( x ) ⋅ g' ( x )
[ g( x ) ] 2
25
In particolare, se f ( x ) = 1 abbiamo la derivata del reciproco:
h( x ) =
1
g( x )
⇒ h' ( x ) = −
g' ( x )
[ g( x ) ] 2
Non viene data la dimostrazione.
Esempi:
1. D[
2.
D[
1
sin  x cos  x 
2
x −1
ln  x 
]=
]=−
cos  x −sin  x 
2
sin  x cos  x 
1
2x⋅ln  x− ⋅ x 2−1
x
ln 2  x 
Come applicazione della regola della derivata del quoziente, calcoliamo le
derivate delle funzioni goniometriche tg(x) e ctg(x):
D[tan  x]=D[
D[ctg x ]=D[
sin  x 
cos  x 
cos  x
sin x 
]=
]=
cos 2  x sin 2  x 
2
cos  x
1
= cos 2  x 
−sin2  x −cos 2  x 
2
sin  x 
1tan 2  x
−1
Esercizi per casa:
Calcolare le derivate delle seguenti funzioni
1.
2.
3.
2ln x 
x
2
sin  x 
2
−1ctg  x 
=
2
x 2tan x 
sin  x
x sin  x 
ex
26
Oltre a queste 3, ho chiesto ai ragazzi di farne altre 3 a piacere tra gli esercizi
proposti dal libro di testo.
OTTAVA LEZIONE: DERIVATA DELLA FUNZIONE COMPOSTA
Nella prima parte è stata fatta la correzione degli esercizi per casa e ho
interrogato.
Nella seconda parte ho spiegato la regola di derivazione di una funzione
composta:
FUNZIONI COMPOSTE
ho richiamato brevemente il concetto di funzione composta considerando un
esempio:
2
la funzione y=e x 1 è l'esponenziale del polinomio x 21 , che a sua volta è una
funzione di x. Se poniamo z  x =x 21 , si ha che y=e z  x , cioè la y è funzione di
un'altra funzione.
In generale, data una funzione z=g(x) nella variabile x, che ha come dominio
l'insieme A e codominio l'insieme B, e y=f(z) una funzione della variabile z che
ha B come dominio e C come codominio, la funzione y=f(g(x)) si dice
funzione composta e f(z) e g(x) si dicono componenti della y.
Teorema
Se la funzione g è derivabile nel punto x, e la funzione f è derivabile nel punto
z=g(x), allora la funzione composta y=f(g(x)) è derivabile in x e la sua
derivata è il prodotto delle derivate di f rispetto a z e di g rispetto a x:
D[ f g  x ]= f ' z ⋅g '  x  con z=g x
La dimostrazione viene omessa.
La parte più difficile di questo argomento è sicuramente riconoscere le
funzioni componenti. Per questo ho ritenuto di dover spendere molto tempo
su esempi ed esercizi.
27
Esempi
1. D[ln x 22]
2
g  x= x 2=z , f  z=ln  z  :
1
2x
2
D[ln x 2]= ⋅2x= 2
z
x 2
2. D[cos  x 3] , g  x =x 3 , f  z=cos z , D[cos  x 3]=−sin  x 3⋅3x 2
Il teorema precedente può essere esteso al caso di funzioni composte da più
di due componenti.
Esempio 1:
D[sin2  x 2 −1] :
g x =x 2 −1 , h  z=sin  z , z=g  x , f t =t 2 , t=sin z 
D[sin2  x 2−1]=2 sin  x 2−1⋅cos  x 2 −1⋅2x
Esercizi per casa:
Ho chiesto ai ragazzi di fare 6 derivate di funzioni composte, scegliendole
dagli esercizi del libro di testo.
NONA LEZIONE: ESERCIZI SULLA DERIVATA DELLA FUNZIONE COMPOSTA E VERIFICHE ORALI
DECIMA LEZIONE: DERIVATA DI F(X)G(X) E DELLA FUNZIONE INVERSA
Dopo aver corretto gli esercizi per casa, ho spiegato il metodo per derivare la
funzione f(x)g(x) utilizzando la regola di derivazione della funzione composta
introdotta nella lezione precedente:
Siano f(x) e g(x) due funzioni derivabili, e sia f(x)>0.
Voglio derivare y=f(x)g(x) : per prima cosa, calcoliamo i logaritmi dei due
membri:
g  x
ln  y=ln [ f  x
]=g  x ⋅ln[ f  x ]
ora calcolo la derivata di entrambi i membri, applicando la regola della
derivata della funzione composta:
28
1
y'
⋅y=g '  x ⋅ln[ f  x ]g x⋅
f 'x
f x
 y ' =y⋅[ g '  x ⋅ln[ f  x ]g  x ⋅
f ' x
f  x
]
ma poichè y=f(x)g(x) :
g x
y ' = f  x  ⋅[g '  x ⋅ln[ f  x ]g x⋅
f ' x
f x
]
DERIVATA DELLA FUNZIONE INVERSA
D'accordo con la tutor, abbiamo deciso di non dedicare troppo tempo alla
derivata della funzione inversa, ma solo di richiamare il significato di funzione
inversa e dare, senza dimostrazione, le derivate delle funzioni inverse delle
funzioni goniometriche fondamentali.
Teorema
Data la funzione y=f(x) definita e invertibile nell'intervallo I, x=f-1(y) è la sua
funzione inversa. Se f(x) è anchde derivabile, e con derivata diversa da 0 in
ogni punto di I, allora anche f-1(y) è derivabile e vale la relazione:
D[ f −1  y ]=
1
, x = f −1  y
f ' x
.
Come applicazione di questo teorema, si possono calcolare le derivate delle
funzioni goniometriche inverse, di cui mi sono limitato a dare la formula:
D[arcsin  x ]=
D[arccos x ]=
1
 1−x
2
−1
 1−x
D [arctan  x]=
D [arccot  x]=
2
1
1x 2
−1
1x 2
Esempi
29
1
⋅2x=
⋅2x
2
1− x 1
x
1
1
D[lnarctan  x]=
⋅
2
arctan  x  1x
1
1
D[ arcsin x]=
⋅
2
2 arcsin  x 1−x
D[arcsin  x 2 1]=
1

2


Esercizi per casa:
D[2 arcsin 1−x 2 ]
arccos x 
D[
]
arcsin  x 
x 2−1
D[arccot 2
]
x 1
come esercizio per casa ho anche chiesto di ricavare, sfruttando il teorema
fatto, la derivata dell'arcoseno e dell'arcotangente.
30
UNDICESIMA LEZIONE: SIGNIFICATO FISICO DI DERIVATA
Per motivi di tempo, abbiamo concordato con la tutor di non perdere molto
tempo sulle applicazioni delle derivate alle altre discipline, in particolare alla
fisica (con mio grosso dispiacere!).
Perciò mi sono limitato ad introdurre l'applicazione del concetto di derivata ad
un
moto
unidimensionale:
in
particolare
ho
definito
la
velocità
e
l'accelerazione.
Per prima cosa, ho definito le derivate di ordine superiore semplicemente
dicendo che: la derivata di ordine n di una funzione f(x) è la funzione che si
ottiene applicando n volte l'operazione di derivazione a f(x).
Velocità e accelerazione
In fisica, lo spazio percorso da un corpo durante un moto unidimensinale è
esprimibile come una funzione della variabile 'tempo'. Questa funzione viene
chiamata legge oraria,
si indica con
s t  , e rappresenta lo spazio
percorso, s, in funzione della variabile indipendente t.
Ad esempio, nel moto uniforme la legge oraria è
s( t ) = s 0 + vt
con s 0 spazio al tempo t = 0 e v velocità costante.
Nel moto uniformemente accelerato invece la legge oraria è
1
s( t ) = s 0 + v0 t + at 2
2
con s 0 e v0 spazio e velocità al tempo t = 0 e a accelerazione costante.
31
Nel grafico seguente è riportata la parabola di equazione
1
s=1− g t 2 , con
2
g=9.8m/s. Questa parabola rappresenta, per s>0 e t>0, la legge oraria del
moto uniformemente accelerato nel caso in cui
s 0 =1, v 0=0 e a=−g
(che può
rappresentare, ad esempio, la caduta di un grave inizialmente fermo da
un'altezza di 1 metro).
Il rapporto incrementale di questa
funzione relativo ad un intervallo di
tempo generico è:
s
t
, cioè è il rapporto tra lo spazio
percorso e il tempo ∆t impiegato a
percorrerlo. Ma questa è anche la
definizione di velocità media relativa all'intervallo di tempo Δt:
vm =
∆s s( t + ∆t ) − s( t )
=
∆t
∆t
Passando al limite del rapporto incrementale al tendere a zero dell’incremento
∆t , questo limite, se esiste, rappresenta la velocità istantanea che possiede il
punto materiale all’istante t.
vi = lim
∆t → 0
s( t + ∆t ) − s( t )
= s' ( t ) .
∆t
Quindi la velocità istantanea è la derivata della funzione che
rappresenta la legge oraria calcolata per l’istante che si sta
considerando.
Esempio
Due corpi si muovono seguendo le leggi orarie
s 1=2 t 2 −t e s 2=
−1
2
t 29 t
Calcolare in quale istante il primo ha velocità doppia del secondo.
Da quanto detto, le velocità dei due corpi in un istante generico saranno:
32
.
v 1=4 t−1 e v 2=−t9 . Nell'istante che cerchiamo,
quindi
4t−1=−2t 18 , da cui si trova che
In maniera analoga, se una funzione
v1
è il doppio di
v2 ,
t=19/6 secondi.
v=v t
rappresenta la legge con cui
varia la velocità al variare del tempo t, la grandezza accelerazione media è
definita dal rapporto a m =
è
avvenuta
tale
∆v
fra la variazione della velocità e il tempo nel quale
∆t
variazione, cioè l’accelerazione media è
il
rapporto
incrementale della funzione v(t). Passando al limite del rapporto incrementale,
al tendere a zero dell’incremento ∆t , questo limite, se esiste, rappresenta
l’accelerazione istantanea che possiede il punto materiale all’istante t:
a i = lim
∆t →0
v( t + ∆t ) − v( t )
= v' ( t ) .
∆t
Poiché, da quanto visto precedentemente, v( t ) = s' ( t ) , possiamo dedurre che
a ( t ) = v ' ( t ) = s' ' ( t ) .
L’accelerazione istantanea è quindi la derivata prima della funzione
velocità rispetto al tempo, ma anche la derivata seconda dello spazio
rispetto al tempo.
Esempio
Data la legge oraria s( t ) = 4 t , calcolare l’accelerazione all’istante t = 4 s .
Abbiamo: s' ( t ) = 4 e s' ' ( t ) = 0 , per cui vi = 4 m / s e a i = 0 m / s 2 .
L’accelerazione risulta nulla, infatti la legge assegnata è quella di un moto
uniforme (legge oraria lineare, velocità costante, accelerazione nulla).
Esempio
Consideriamo adesso la legge oraria s( t ) = 5t + 2t 2 e calcoliamo l’accelerazione
all’istante t = 2 s . Si ha: s' ( t ) = 5 + 4t e s' ' ( t ) = 4 , per cui vi = 13 m / s e a i = 4 m / s 2 .
33
L’accelerazione risulta costantemente uguale a 4 m / s 2 ; la legge del moto
assegnata è infatti quella di un moto uniformemente accelerato.
Infine esaminiamo la legge oraria s( t ) = 3t 3 − 2 t + 4 e calcoliamo l’accelerazione
all’istante
s' ( t ) = 9t 2 − 2
t = 2 s:
e
s' ' ( t ) = 18t ;
per
cui
vi = s' ( 2) = 34 m / s
e
a i = s' ' ( 2) = 36 m / s 2 .
In questo caso il moto non ha un’accelerazione costante ma variabile.
DODICESIMA LEZIONE: VERIFICA SOMMATIVA
Obiettivi da verificare:
1. Conoscere
la
definizione di
derivata
come
limite del rapporto
incrementale;
2. Conoscere i vari punti di non derivabilità;
3. Saper applicare le regole di derivazione;
4. Saper trovare l'equazione della retta tangente a una funzione in un
punto di ascissa data;
La prova è composta da 4 esercizi, ognuno dei quali mirato a verificare,
nell'ordine, gli obiettivi indicati sopra:
Testo della verifica
Esercizio 1:
Calcolare, con il limite del rapporto incrementale, la derivata della funzione
f(x) nel punto x0 indicato a fianco:
f  x =ln x 3 x 0 =0
Esercizio 2:
Calcolare, con il limite del rapporto incrementale, la derivata destra e sinistra
delle seguenti funzioni nel punto x0 indicato a fianco.
Dire se la funzione è derivabile nel punto e, se non lo è, dire di che tipo di non
derivabilità si tratta:
34
a)
f  x =x 2−∣x∣ x 0=0
b)
f  x =  x −32 x 0=3
3

Esercizio 3:
Calcolare, usando le regole di derivazione, le derivate di 6 delle seguenti
funzioni:
a. x2
x
b. 25 x 2 
2
1
x
−e2
c. x log 2 x2x
d. e x 3x cos x
e. sin2 x
f. ln x 3
3x2 −1
g. ln
x
2
h. 2 tan  x 31
Esercizio 4:
Data la funzione
y=k x 2−k −1 x−k3 , scrivi l'equazione della retta tangente
al suo grafico nel punto di ascissa x=3, e determina k in modo che passi per il
punto (1; 2).
35
Tabella di valutazione
Esercizio
Punteggio
1
0­0.75 fino alla scrittura corretta del limite del rapporto incrementale;
0.75­2 calcolo corretto del limite.
2 a.
2 b.
0­1.4 fino al calcolo corretto della derivata destra e sinistra; 1.4­2 identificazione corretta del tipo di non derivabilità.
Idem a 2 a.
3 1 per ogni derivata calcolata correttamente
4
0­1 scrittura corretta dell'equazione della retta tangente
1­2 determinazione corretta di k
36
Osservazioni sulla verifica
Il punteggio totale della verifica è 14, che ho normalizzato a 7 partendo da un
voto massimo di 9 a un voto minimo di 2. Per quelli che avessero calcolato
correttamente più di 6 delle 8 derivate richieste dall'esercizio 3, avevo previsto
un voto massimo di 10, ma nessuno ci è riuscito.
I ragazzi presenti erano 22. Ci sono state 11 sufficienze, 10 insufficienze, di
cui 3 gravi (voto inferiore a 4.5) e 1 compito consegnato in bianco.
Di seguito descrivo, esercizio per esercizio, le maggiori difficoltà incontrate
dai ragazzi:
•
Nell'esercizio 1 quasi tutti hanno scritto correttamente il limite del
rapporto incrementale, ma diversi poi hanno sbagliato il calcolo del
limite. Questo è forse dovuto al fatto che i ragazzi non si erano ripassati
i limiti notevoli, assunti come prerequisito;
•
Nell'esercizio 2, molti hanno portato a termine correttamente il calcolo
della derivata destra e sinistra, ma alcuni hanno confuso la derivata
destra con la sinistra perché hanno scritto in maniera sbagliata il valore
assoluto. Diversi hanno anche scritto in maniera imprecisa il tipo di
discontinuità: due persone, dopo aver scritto correttamente il valore
della derivata destra e della derivata sinistra in x0, hanno scritto frasi
del tipo “siccome i limiti sono diversi, i punti sono angolosi” (???).
•
Nell'esercizio 3 le derivate che hanno dato maggiori problemi sono
quelli con i logaritmi e le potenze, che hanno evidenziato che i ragazzi
hanno difficoltà ad applicare le proprietà delle potenze e dei logaritmi.
•
L'esercizio 4 è stato eseguito correttamente da molti. Gli errori sono
soprattutto banali errori di calcolo algebrico.
37
Bibliografia:
•
L. Lamberti, L. Mereu, A. Nanni, 'Matematica tre', ETAS libri
•
M. Bergamini, A. Trifone, G. Barozzi, 'Moduli blu di matematica. Modulo
V+W: Derivate e studi di funzione + integrali', Zanichelli
•
N.Dodero, P.Baroncini, R. Manfredini, ‘Elementi di matematica’, edizione
per i licei scientifici a indirizzo sperimentale, Volume 3, Ghisetti e Corvi
Editori.
38