CLASSE : 1° TURISTICO MATEMATICA (Ramella) Situazione di

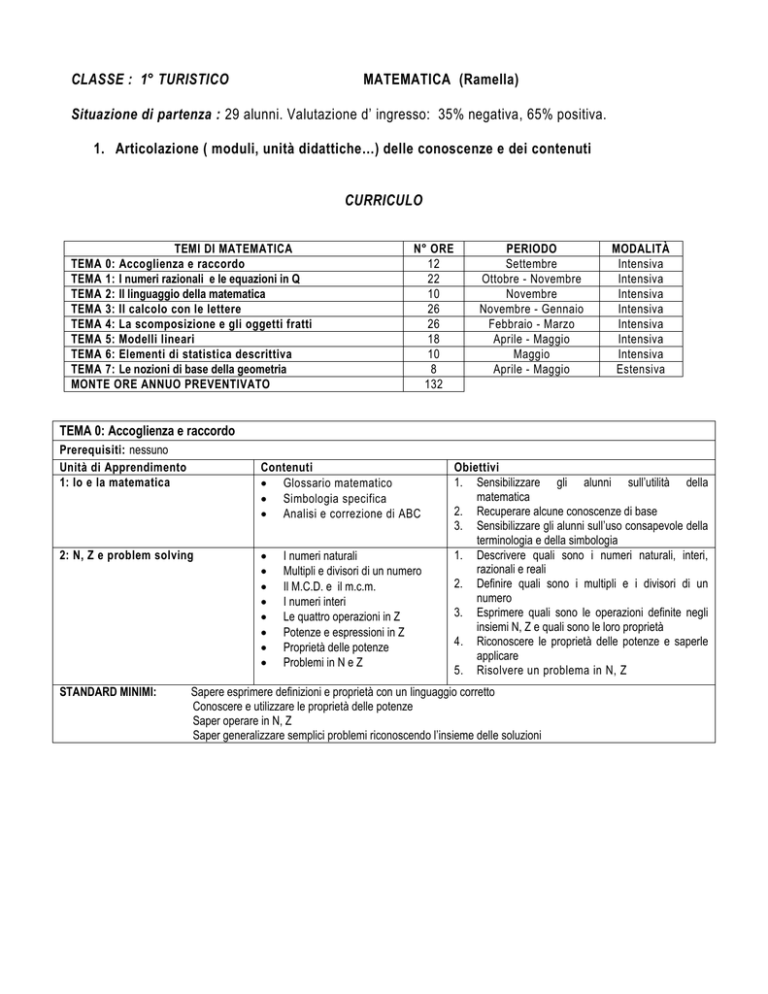
CLASSE : 1° TURISTICO
MATEMATICA (Ramella)
Situazione di partenza : 29 alunni. Valutazione d’ ingresso: 35% negativa, 65% positiva.
1. Articolazione ( moduli, unità didattiche…) delle conoscenze e dei contenuti
CURRICULO
TEMI DI MATEMATICA
TEMA 0: Accoglienza e raccordo
TEMA 1: I numeri razionali e le equazioni in Q
TEMA 2: Il linguaggio della matematica
TEMA 3: Il calcolo con le lettere
TEMA 4: La scomposizione e gli oggetti fratti
TEMA 5: Modelli lineari
TEMA 6: Elementi di statistica descrittiva
TEMA 7: Le nozioni di base della geometria
MONTE ORE ANNUO PREVENTIVATO
N° ORE
12
22
10
26
26
18
10
8
132
PERIODO
Settembre
Ottobre - Novembre
Novembre
Novembre - Gennaio
Febbraio - Marzo
Aprile - Maggio
Maggio
Aprile - Maggio
MODALITÀ
Intensiva
Intensiva
Intensiva
Intensiva
Intensiva
Intensiva
Intensiva
Estensiva
TEMA 0: Accoglienza e raccordo
Prerequisiti: nessuno
Unità di Apprendimento
1: Io e la matematica
Contenuti
 Glossario matematico
 Simbologia specifica
 Analisi e correzione di ABC
2: N, Z e problem solving
STANDARD MINIMI:








I numeri naturali
Multipli e divisori di un numero
Il M.C.D. e il m.c.m.
I numeri interi
Le quattro operazioni in Z
Potenze e espressioni in Z
Proprietà delle potenze
Problemi in N e Z
Obiettivi
1. Sensibilizzare gli alunni sull’utilità della
matematica
2. Recuperare alcune conoscenze di base
3. Sensibilizzare gli alunni sull’uso consapevole della
terminologia e della simbologia
1. Descrivere quali sono i numeri naturali, interi,
razionali e reali
2. Definire quali sono i multipli e i divisori di un
numero
3. Esprimere quali sono le operazioni definite negli
insiemi N, Z e quali sono le loro proprietà
4. Riconoscere le proprietà delle potenze e saperle
applicare
5. Risolvere un problema in N, Z
Sapere esprimere definizioni e proprietà con un linguaggio corretto
Conoscere e utilizzare le proprietà delle potenze
Saper operare in N, Z
Saper generalizzare semplici problemi riconoscendo l’insieme delle soluzioni
TEMA 1: I numeri razionali e equazioni in Q
Prerequisiti: sapere la tavola pitagorica dei numeri e l’ordine dei naturali, saper fare le quattro operazioni
Unità di Apprendimento
Contenuti
Obiettivi
1: I numeri razionali
 Dalle frazioni ai numeri razionali
Conoscenze
 Confronto di numeri razionali
1. Descrivere quali sono i numeri razionali
 Le operazioni nell’insieme Q
2. Definire le potenze e conoscere le principali
 I razionali ed i decimali
proprietà
3. Conoscere il concetto di percentuale e quello di
 Le potenze in Q
proporzione
 Rapporti, proporzioni e percentuali
4. Descrivere che cos’è un insieme, una proposizione
 Problemi in Q
Abilità
1. Rappresentare numeri interi e razionali sulla retta
2. Confrontare numeri interi e razionali
3. Trasformare frazioni in numeri decimali o percentuali
e viceversa
4. Eseguire le quattro operazioni in Q e
semplificare espressioni numeriche
5. Calcolare potenze e applicare le principali
proprietà
2: Equazioni in Q
 Le identità e le equazioni
6. Tradurre da frase a espressione e viceversa
 I principi di equivalenza
7. Risolvere un problema in N, Z e in Q
 Le equazioni intere numeriche di 8. Eseguire operazioni tra insiemi
primo grado in N, Z e Q
9. Risolvere semplici equazioni in N
 Problemi in N, Z e Q
10. Formalizzare e risolvere problemi di primo grado
STANDARD MINIMI:
Sapere esprimere definizioni e proprietà con un linguaggio corretto
Conoscere e utilizzare le proprietà delle potenze
Saper operare in Q
Saper generalizzare semplici problemi riconoscendo l’insieme delle soluzioni
Conoscere definizioni e principi di equivalenza
Saper distinguere le varie tipologie di equazioni
Saper risolvere le equazioni in N, Z e Q
Saper costruire un modello matematico per risolvere semplici problemi
COMPETENZE: Padroneggiare le tecniche e le procedure di calcolo nei vari insiemi numerici e saperle rappresentare in
contesti reali
Tradurre dal linguaggio verbale a un linguaggio simbolico e viceversa
Padroneggiare il linguaggio della matematica e sapersi esprimere correttamente
Individuare strategie appropriate per la risoluzione dei problemi
TEMA 2: Il linguaggio della matematica
Prerequisiti: operazioni fondamentali, percentuali, piano cartesiano
Unità di Apprendimento
Contenuti
Obiettivi
1: Insiemi e operazioni
 Gli insiemi e la loro rappresentazione Conoscenze
 I sottoinsiemi
1. Conoscere il significato di insieme
 Le operazioni tra insiemi
2. Definire insiemi e sottoinsiemi
 Il prodotto cartesiano
3. Definire le operazioni fra insiemi
 Insiemi in contesto geometrico
Abilità
 Insiemi di soluzioni
1. Rappresentare un insieme
 Gli insiemi come modello per risolvere 2. Operare con gli insiemi
problemi
3. Risolvere problemi con gli insiemi
 I connettivi logici AND e OR
STANDARD MINIMI:
Saper operare con gli insiemi, anche su semplici problemi pratici
COMPETENZE: Padroneggiare le tecniche e le procedure di calcolo nei vari insiemi numerici e saperle rappresentare
in contesti reali
Tradurre dal linguaggio verbale a un linguaggio simbolico e viceversa
Padroneggiare il linguaggio della matematica e sapersi esprimere correttamente
Individuare strategie appropriate per la risoluzione dei problemi
TEMA 3: Il calcolo con le lettere
Prerequisiti: gli insiemi numerici; le proprietà delle operazioni e delle potenze
Unità di Apprendimento
Contenuti
Obiettivi
1: Monomi
 Il calcolo letterale
Conoscenze
 I monomi
1. Definire un monomio, un polinomio
 Addizione e sottrazione di monomi
2. Conoscere i principali prodotti notevoli
 Moltiplicazione, potenza e divisione 3. Conoscere l’algoritmo della divisione tra polinomi
tra monomi
4. Conoscere la regola di Ruffini
5. Conoscere il teorema del resto e di Ruffini
 M.C.D. e m.c.m. tra monomi
2: Polinomi
Abilità
 I polinomi: caratteristiche
 Operazioni tra i polinomi
1. Eseguire operazioni tra monomi e polinomi
 Prodotti notevoli
2. Utilizzare i prodotti notevoli
3. Eseguire divisioni tra polinomi
3: Divisibilità di polinomi
 Divisione tra polinomi
4. Utilizzare il teorema del resto
 La regola di Ruffini
5. Risolvere problemi con il calcolo letterale
 Teorema del resto e di Ruffini
STANDARD MINIMI:
Semplificare espressioni monomie
Saper calcolare i prodotti notevoli con coefficienti interi
Saper applicare la regola di Ruffini
COMPETENZE: Tradurre dal linguaggio verbale a un linguaggio simbolico e viceversa
Acquisire la consapevolezza dell’uso delle lettere per generalizzare, rappresentare relazioni,
formalizzare e risolvere problemi
TEMA 4: Scomposizione e oggetti fratti
Prerequisiti: gli insiemi numerici; il calcolo letterale
Unità di Apprendimento
Contenuti
Obiettivi
1: Scomposizioni
 Raccoglimenti totali e parziali
Conoscenze
 Riconoscimento di prodotti notevoli
1. Definire cosa si intende per polinomio riducibile o
 Somma e differenza dei cubi
irriducibile
 Scomposizione di un trinomio di 2. Definire i concetti di M.C.D. e m.c.m. tra polinomi
secondo grado
3. Definire le condizioni di esistenza di una frazione
algebrica
 Scomposizione con Ruffini
 M.C.D. e m.c.m. tra polinomi
Abilità
2: Frazioni algebriche
 Le frazioni algebriche e la loro 1. Scomporre un polinomio
esistenza
2. Determinare M.C.D. e m.c.m. tra polinomi
 Semplificazione di una frazione 3. Operare con le frazioni algebriche
algebrica
 Operazioni con le frazioni algebriche
STANDARD MINIMI:
Saper scomporre polinomi con il riconoscimento di una sola tecnica
Saper lavorare con le frazioni algebriche in semplici espressioni con tutte le operazioni senza gravi errori
concettuali
TEMA 5: Modelli lineari
Prerequisiti: gli insiemi numerici; il calcolo letterale
Unità di Apprendimento
Contenuti
1: Equazioni intere e fratte
 Richiamo sulle soluzioni numeriche
intere
 Particolari equazioni di grado
superiore al primo
 Problemi che hanno come modello
un’equazione lineare
 Le equazioni fratte
 Semplici equazioni letterali
 Problemi che hanno come modello
equazioni lineari intere e fratta
STANDARD MINIMI:
Obiettivi
Conoscenze
1. Conoscere i principi di equivalenza
2. Conoscere il significato di soluzione
3. Conoscere il significato di dominio di una equazione
Abilità
1. Risolvere equazioni intere di pirimo grado
2. Saper applicare la legge dell’annullamento del
prodotto
3. Determinare il dominio di una equazione fratta
4. Risolvere un’equazione fratta
5. Discutere semplici equazioni letterali
6. Risolvere problemi che hanno come modello
equazioni
Saper risolvere semplici equazioni fratte
Saper costruire un modello matematico per risolvere semplici problemi
COMPETENZE: Individuare strategie per risolvere problemi che hanno c ome modello equazioni, disequazioni lineari
TEMA 6: Elementi di statistica descrittiva
Prerequisiti: operazioni fondamentali, percentuali, piano cartesiano
Unità di Apprendimento
Contenuti
1: La statistica: elaborazione  Cos’è la statistica
e rappresentazione dei dati
 Fasi di un’indagine statistica
 La distribuzione di frequenze
 La distribuzione per classi
 La rappresentazione grafica
2: Valori di sintesi e indici di
variabilità


I principali valori di sintesi: media,
moda e mediana
Gli indici di variabilità: scarto,
deviazione standard e varianza
Obiettivi
Conoscenze
1. Conoscere il significato dei termini statistici
2. Leggere una tavola ISTAT
3. Definire e riconoscere i grafici statistici
4. Definire i vari tipi di media
5. Definire i principali indici di variabilità
Abilità
1. Utilizzare correttamente la terminologia relativa alla
statistica
2. Progettare un’indagine statistica
3. Rappresentare graficamente dei dati, scegliendo il
grafico più adatto
4. Calcolare una media
5. Scegliere la media che meglio sintetizza dei dati
6. Calcolare i principali indici di variabilità
STANDARD MINIMI:
Riconoscere le fasi di un’indagine statistica.
Saper analizzare semplici situazioni, saperle rappresentare e descrivere con gli strumenti matematici.
COMPETENZE: Analizzare dati e interpretarli sviluppando deduzioni e ragionamenti sugli stessi anche con l’ausilio di
rappresentazioni grafiche, usando consapevolmente gli strumenti di calcolo e le potenzialità offerte da applicazioni specifiche di tipo
TEMA 7: Le nozioni di base della geometria
Prerequisiti: saper utilizzare: riga, squadra e compasso, teoria degli insiemi, elementi di logica
Unità didattica
Contenuti
Obiettivi
1: Il piano euclideo
 Elementi
fondamentali
della Conoscenze
geometria razionale (concetti primitivi, 1. Conoscere il significato di ente primitivo, assioma,
assiomi, definizioni e teoremi)
definizione e teorema
 Segmenti, semirette e poligonali
2. Definire segmenti, angoli e poligoni e conoscerne le
 Angoli
caratteristiche
 Poligoni
Abilità
1. Operare con i segmenti e gli angoli
2. Saper rappresentare correttamente le figure
geometriche
3. Saper dimostrare un semplice teorema
STANDARD MINIMI:
Conoscere le principali definizioni
Effettuare semplici congetture, anche con l’uso di Geogebra
COMPETENZE: Rappresentare, confrontare e analizzare le figure geometriche del piano
Ragionare correttamente e dimostrare semplici congetture
Saper costruire deduzioni logiche e fare congetture per dimostrare la tesi partendo dall’ipotesi
1. Attività didattiche e formative, impostazione metodologia.
Dal punto di vista metodologico è fondamentale un rapporto organico tra didattica in aula, per la spiegazione della teoria e
l’applicazione mediante esempi significativi, e attività di tipo laboratoriale per la realizzazione di modelli e la sperimentazione di leggi. Si
procederà quindi all’accumulazione di conoscenze anche attraverso processi di realizzazione, sfruttando la metodologia del problem
solving.
Verranno utilizzati quindi i seguenti metodi:
o far pervenire al possesso delle conoscenze partendo, quando possibile, da situazioni reali, non ancora organizzate, così da
stimolare l’abitudine a costruire modelli;
o privilegiare momenti di scoperta e di successive generalizzazioni a partire da casi semplici, così da favorire l’acquisizione di
comportamenti produttivi;

Strumenti metodologici:
o di lavoro:
 libri di testo
 hardware e software di laboratorio
 appunti forniti dal docente
o
di osservazione:
 correzione compiti a casa
 verifiche formative
 dialogo con la classe
 schede di monitoraggio di attività di laboratorio
Le lezioni, organizzate prevalentemente con modalità frontale-interattiva, avranno luogo principalmente in classe ma anche in laboratorio
e saranno del seguente tipo:
o lezioni frontali-interattive per formalizzare concetti e regole e scoprire nessi, relazioni e leggi;
o lezioni teorico-pratiche in laboratorio per illustrare metodi e processi;
o esercitazioni per sviluppare le conoscenze acquisite;
o esercitazioni in laboratorio per implementare simulazioni e algoritmi mediante applicativi;
o eventuali attività di apprendimento cooperativo per sviluppare abilità sociali e cognitive;

Libro/i di testo in uso
Ilaria Fragni
Percorso Matematica 1
Cedam
2. Tipologie di verifica; griglie di correzione e di valutazione.
 Valutazione e strumenti di verifica
La valutazione verrà effettuata mediante: verifiche orali parziali al termine di una o più unità didattiche; verifiche scritte intermedie e/o di
fine modulo; test. Saranno inoltre valutati esercizi assegnati come compiti a casa. Le verifiche scritte saranno di tipo semi strutturato e
potranno contenere item di vario tipo oppure con quesiti a risposta aperta, esercizi. Per ognuna verrà specificato il punteggio grezzo
minimo per raggiungere la sufficienza.

Criteri di valutazione
o Prove scritte:
 Comprensione del testo
 Rigorosità nello svolgimento degli esercizi
 Corretto uso dei simboli e della terminologia
specifica
 Costruzione corretta e precisa di schemi,
diagrammi e grafici
o Prove orali:
 Pertinenza della risposta



Uso di un linguaggio appropriato e della
terminologia tecnica
Capacità di collegamento
Sicurezza nell’argomentazione, anche mediante
esempi significativi
Le valutazioni verranno espresse in decimi, usando l’intervallo 2-10.
Il voto 1 verrà usato per la consegna in bianco dei compiti in classe e per il rifiuto all’interrogazione orale.

Numero minimo di verifiche: almeno due verifiche per il trimestre e quattro per il pentamestre sotto forma di verifiche scritte, interrogazioni (eventualmente come
sintesi di interrogazioni parziali) e test sulle conoscenze, anche parziali
VEDI GRIGLIA DI VALUTAZIONE E CORREZIONE :
GRIGLIA DI VALUTAZIONE
INDICATORI
CONOSCENZE
LIVELLI DI PRESTAZIONE IN % E DESCRITTORI
LP< 10%
10%<=LP<=30%
31%<=LP<=49%
50%<=LP<=61%
Nulle
Scarse
Frammentarie
Essenziali
ABILITA’
E
Esegue compiti
Nulle
COMPETENZE
ESPOSIZIONE /
TERMINOLOGIA
VOTO
semplici con molti
errori
Esegue compiti
semplici con errori
Esegue compiti
semplici con pochi
errori
62%<=LP<=74%
75%<=LP<=95%
>9,5%
Complete ma poco
Complete ma non
Complete e
approfondite
tutte approfondite
approfondite
Esegue compiti
Esegue compiti
Esegue compiti
semplici senza errori
complessi su
complessi su
e compiti complessi
problematiche
problematiche
con errori
note
nuove
Appropriata
Formale
Articolata
Completa
da 8 a 9,5
10
Nulle
Scarsa e scorretta
Imprecisa
Essenziale
Appropriata
da1 a 2,5
da3- a 4+
da 4,5 a 6-
da 6 a 7-
da 7 a 8-
VOTI POSSIBILI 1 2 2+ 2,5 3- 3 3+ 3,5 4- 4 4+ 4,5 5- 5 5+ 5,5 6- 6 6+ 6,5 7- 7 7+ 7,5 8- 8 8+ 8,5 9 9- 9,5 10- 10
Si ricorda che il LIVELLO DI SUFFICIENZA è rappresentato dalla metà del punteggio.
NELLE SINGOLE PROVE VERRA’ USATA UNA GRIGLIA DI CORREZIONE COME LA SEGUENTE, RELATIVA ALLE
CONOSCENZE E/O ABILITA’ E COMPETENZE A SECONDO DELLA TIPOLOGIA DI VERIFICA.
ITEM
C1
C2
C3
C4
C5
A1
A2
A3
A4
A5
TOT PUN
CONOSC.
PUN
OTT
LP
CON.
VOTO ORALE
2 + ( LP * 8/100)
%
PUN_DISP
TOT PUN
ABILITA’
PUN_OTT
PUN
OTT
LP
ABIL.
%
VOTO SCRITTO
2 + ( LP * 8/100)