Lezione 3_formazione complessi Archivo - e

Formazione di complessi
Prof.ssa A. Gentili
Struttura degli ioni complessi
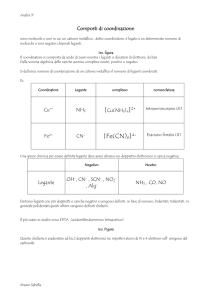
Gli ioni complessi sono formati da un catione metallico legato a un
numero di anioni come OH-, Cl-, CN-, SCN-, o di molecole neutre come
H2O, NH3., detti ligandi.
Il numero dei ligandi rappresenta il numero di coordinazione del
complesso in esame. Per esempio Ag(NH3)2+ e Cu(NH3)4+ hanno come
numeri di coordinazione rispettivamente 2 e 4.
I complessi possono essere cationici, anionici o neutri, in base alla
carica complessiva dello ione ottenuto.
I ligandi si comportano come basi di Lewis, perché hanno disponibili
doppietti elettronici; i coordinatori metallici, invece, si comportano
come acidi di Lewis a causa della carenza elettronica degli orbitali
esterni.
Sono chiamati chelati i complessi con struttura ad anello a 5 o 6
termini.
Formazione di complessi metallo-legante
La formazione di un complesso
metallo-legante è un particolare tipo
di reazione acido-base.
In realtà, prima che abbia inizio la
formazione del complesso del Cu2+
con l’ammoniaca , in soluzione sono
presenti dei complessi tra gli ioni del
Cu2+ e l’acqua, cioè Cu(H2O)62+.
Quando si aggiunge ammoniaca, l’H2O (base di Lewis debole) legata allo ione Cu2+ è sostituita da NH3
(base di Lewis più forte):
Eq 1
Continuando ad aggiungere ammoniaca, anche le altre 5 molecole di H2O vengono sostituite da NH3: le
prime 4 a basse concentrazioni di NH3 le altre 2 solo a concentrazioni molto elevate:
Eq 2
Ognuna di queste reazioni presenta due coppie di reazioni acido-base di Lewis. Nell’eq. 1,
Cu(H2O)62+ e NH3 sono rispettivamente l ’acido e la base di Lewis dalla parte dei reagenti,
mentre Cu(NH)3(H2O)52+ e H2O sono l’acido e la base di Lewis dalla parte dei prodotti.
Leganti monodentati
Tutte le sostanze in grado di donare un solo doppietto elettronico
prendono il nome di leganti monodentati o leganti semplici.
Per evitare che le equazioni di formazione dei complessi siano troppo complicate, si
omettono le molecole d’acqua legate allo ione metallico, così le eq 1 e 2 diventano:
e
Anche quando l’acqua viene omessa, si deve ricordare che questo
solvente può svolgere un ruolo attivo durante la formazione dei
complessi metallo-legante. Poiché l’acqua può agire da base di Lewis,
essa è in grado d’influenzare la capacità con cui uno ione metallico
reagisce con un legante come l’ammoniaca.
Maggiore è la forza del legante che agisce da base di Lewis, maggiore
sarà la facilità con cui questo legante riuscirà a rimpiazzare le
molecole d’acqua che interagiscono con lo ione metallico.
Confrontando l’elenco degli ioni metallici e dei leganti in tabella 9.1, ci
ricordiamo che alcuni di essi formano dei sali insolubili: per esempio,
Ag+ con Cl- porta alla formazione di AgCl (insolubile), quando si
combinano in un rapporto 1:1. Tuttavia, aggiungendo una maggiore
quantità di Cl- a questo sistema, una parte del precipitato può
ridisciogliersi formando complessi solubili come AgCl2-, AgCl32- e AgCl43. Qualcosa di simile succede quando, combinando OH- con ioni
metallici, si assiste alla formazione sia di un complesso solubile
(AlOH2+, se OH- reagisce con Al3+ in un rapporto 1:1) che di un
precipitato insolubile (come il sale 1:3 Al(OH)3), a seconda della
concentrazione iniziale dei reagenti.
Costanti di formazione dei complessi metallo-legante
Inizialmente lo ione Ni2+ è coordinato con 6 molecole di H2O. Quando si aggiunge NH3, ogni
mole di NH3 sposta una mole di H2O. Ne risulta una serie di sei reazioni sequenziali. Le
relative costanti di equilibrio sono dette costanti di formazione o costanti di stabilità Kfi:
La costante di formazione termodinamica (Kf°) della reazione di addizione di 1
molecola di NH3 allo ione Ni2+ (oppure (Ni(H2O)62+) è descritta dalla seguente
espressione:
Kf

a

a
a
a
Ni(H2O)5(NH3 )2 
Ni(H2O)62 
H 2O
oppure
in forma semplificata
Kf

a

a a
Ni(NH3 )2 
Ni 2 
NH 3
NH 3
La costante di formazione concentrazione-dipendente (Kf) per la stessa reazione è
invece data da:
 Ni(H O) (NH )2  
2
5
3


Kf 
 Ni(H O) 2  NH 
2
6
3


dove

Kf  Kf

 
Ni(NH3 )2 
Ni 2 
NH 3
Anche per le altre reazioni di complessazione si possono scrivere le stesse espressioni
e relative costanti di formazione, le cui unità sono in M-1.
È importante notare in tabella 9.2 che le Kfi diminuiscono man mano che aumenta il
numero di leganti che si coordinano allo ione metallico, per cui l’attacco delle ultime
molecole di legante avviene solo ad alte concentrazioni.
La velocità con cui si forma un complesso tra uno ione
metallico e un legante L dipende sia dalla costante di
associazione del legante alla sfera esterna dello ione
idratato (Kse) che dalla costante di velocità di perdita delle
molecole di H2O dalla sfera di coordinazione dello ione
metallico (K-H2O)
Vformazione complesso = K-H2O [{M(H2O)62+}L]
= K-H2OKse[M(H2O)62+][L]
= Kf [M(H2O)62+][L]
Previsione della distribuzione dei complessi
metallo-legante
La frazione delle specie di una serie di complessi metallo-legante può essere descritta
scrivendo innanzitutto l’espressione del bilancio di massa per tutte le specie presenti in
soluzione contenenti lo ione metallico:
CNi = concentrazione analitica di tutte le specie del Ni =
[Ni2+]+[Ni(NH3)2+]+[Ni(NH3)22+]+[Ni(NH3)32+]+[Ni(NH3)42+]+[Ni(NH3)52+]+[Ni(NH3)62+]
Questa equazione può essere usata insieme alle Kfi per calcolare la frazione α di ciascuna
specie metallica presente ad una determinata concentrazione di legante. Per una data
specie metallica
α = [specie metallica]/[tutte le specie solubili dello ione metallico]
Ad esempio, la frazione di Ni2+ è:
αNi2+= [Ni2+]/[CNi ]=
=[Ni2+]/([Ni2+]+[Ni(NH3)2+]+[Ni(NH3)22+]+[Ni(NH3)32+]+[Ni(NH3)42+]+[Ni(NH3)52+]+[Ni(NH3)62+])
È necessario semplificare questa relazione, correlando la concentrazione dei termini al
denominatore con la concentrazione nota di NH3 (ligando) e le costanti di formazione del
sistema. Rielaborando l’espressione per Kf1 in tabella 9.2 si può dimostrare che
[Ni(NH3)2+] = Kf1 [Ni2+][NH3];
[Ni(NH3)22+] = Kf2 [Ni(NH3)2+] [NH3]; e così via
Con questa procedura si ottengono le relazioni iniziali di equilibrio indicate in tabella 9.5
2
3
4
5
6
In tali equazioni sono ancora presenti troppi termini incogniti. Sostituendo [Ni(NH3)2+] = Kf1
[Ni2+][NH3] nella seconda espressione relativa alla specie [Ni(NH3)22+], si elimina un’incognita
esprimendo [Ni(NH3)22+] in termini di Kf1Kf2 e delle concentrazioni di [Ni2+] e di [NH3].
Continuando per tutte le specie del Ni, si ottiene una nuova serie di equazioni espresse solo in
termini di [Ni2+], [NH3] e delle costanti di formazione del sistema. Notare l’aumento
dell’esponente della [L] e del numero di Kfi che vengono moltiplicate con l’aumentare del
numero di ligandi complessati.
Introducendo βn, costante di formazione complessiva o cumulativa, come il
prodotto delle singole costanti di formazione consecutive si ha:
βn = Kf1 Kf2 Kf3……Kfn
Questa sostituzione porta alle equazioni nella parte destra della tabella 9.5 per il
sistema Ni2+ e NH3.
A questo punto, riprendendo la frazione
αNi2+ = [Ni2+]/[CNi ]=
=[Ni2+]/([Ni2+]+[Ni(NH3)2+]+[Ni(NH3)22+]+[Ni(NH3)32+]+[Ni(NH3)42+]+[Ni(NH3)52+]+[Ni(N
H3)62+])
Bisogna sostituire le concentrazioni delle diverse specie con le espressioni trovate
in tabella 9.5; si ottiene così:
αNi2+ = [Ni2+]/[CNi ]=
=[Ni2+]/([Ni2+]+ β1[Ni2+][NH3]+β2 [Ni2+][NH3]2+ β3 [Ni2+][NH3]3+ β4 [Ni2+][NH3]4+ β5
[Ni2+][NH3]5+ β6 [Ni2+][NH3]6)
Occorre eliminare l’incognita [Ni2+], dividendo numeratore e denominatore per
[Ni2+]. Si ottiene così l’equazione riportata in tabella 9.4. Si può fare lo stesso per
valutare le frazioni α delle altre specie solo in termini di [L] e di β.
Concentrazione di Ni2+ in un eccesso di NH3
[Ni2+]aq=1.00x10-4 M
[NH3]aq=1.0 M
Tra tutte le specie possibili del nichel:
1) quale sarà la frazione di Ni2+ libero all’equilibrio?
2) quale sarà la concentrazione molare di Ni2+ in questa soluzione?
3) Quale sarà la concentrazione in termini di “pNi”, sapendo che pNi=-log([Ni2+])
1) Conoscendo le costanti β1,β2,….β6 (vedi tab 9.5), è possibile calcolare
αNi2+ = [Ni2+]/[CNi ]=
=1/(1+ β1[NH3]+β2 [NH3]2+ β3 [NH3]3+ β4 [NH3]4+ β5 [NH3]5+ β6 [NH3]6
La concentrazione di NH3 (1 M) è nettamente superiore alla [Ni2+] (1.00x10-4 M); pertanto, al
termine della reazione di complessazione, la concentrazione di NH3 sarà all’incirca uguale a
quella iniziale, cioè 1 M. Inoltre, siccome il pH della soluzione è elevato, si può trascurare la
conversione di NH3 in NH4+.
Sostituendo i valori nell’espressione si ha:
αNi2+ = 2.2 x 10-9
2) [Ni2+] = αNi2+ x [CNi ] = (2.2 x 10-9) x (1.00x10-4) = 2.2 x 10-13
3) pNi=-log([Ni2+] = -log(2.2 x 10-13) = 12.66
Quindi, solo una piccolissima parte di ioni Ni2+ libera è presente in soluzione dopo la
complessazione con NH3.
Complessi di agenti chelanti e ioni metallici
Gli agenti chelanti sono leganti caratterizzati da due o più atomi portanti un doppietto
elettronico non condiviso (ad esempio due atomi di azoto o di ossigeno) e separati tra
loro da almeno due o tre gruppi metilenici.
La presenza di questi gruppi -CH2- permette a entrambi gli atomi portanti il doppietto
elettronico di raggiungere e coordinare lo ione metallico, dando luogo ad una struttura
ciclica stabile a 5 o 6 termini.
L’etilendiammina è un agente chelante di uso comune
Gli agenti chelanti possono essere suddivisi in base al numero dei siti di legame per lo ione
metallico. L’etilendiammina, con due siti di legame, è un legante bidentato. Altri agenti
chelanti sono leganti tridentati, tetradentati o, più in generale, polidentati. Tutti formano con
gli ioni metallici un complesso ciclico. Un complesso di questo tipo prende il nome di chelato.
L’effetto chelante
Gli agenti chelanti sono agenti complessanti più efficienti dei leganti monodentati,
perchè caratterizzati da costanti di formazione più grandi.
Per l’etilendiammina e il Ni2+ a 25 °C:
Kf1 = 2,1 x 107
Kf2 = 1,5 x 106
Kf3 = 1,3 x 104
In confronto le prime tre Kfi
Per la reazione di complessazione tra
Ni2+ e NH3 (legante monodentato)
sono molto più piccole e pari a 520,
140 e 46.
Esiste, inoltre, una notevole differenza tra le costati di formazione cumulative.
La costante di formazione cumulativa tra Ni2+ e 3 molecole di etilendiammina è
β3 = Kf1 x Kf2 x Kf3 = 4,1 x 1017.
La costante di formazione cumulativa tra Ni2+ e 6 molecole di NH3 è β6 = 4,1 x 108.
La tendenza degli agenti chelanti a formare complessi più stabili con gli ioni metallici e con
costanti di formazioni cumulative più elevate rispetto ai lenganti monodentati è nota come
effetto chelato.
Dal punto di vista analitico l’uso di agenti chelanti con un’elevata Kf e in grado di reagire in un
rapporto 1:1 con lo ione metallico (per es.EDTA) è estremamente vantaggioso perché si riduce il
numero di specie presenti in soluzione rispetto all’uso di un legante monodentato.
Acido etilendiammico (EDTA)
L’EDTA ha 6 potenziali siti di legame: 2 atomi di azoto e 4 gruppi carbossilici. Questo
significa che ogni molecola di EDTA può formare 6 legami coordinativi con lo stesso
ione metallico. Ne risulta un complesso 1:1 a elevata stabilità una struttura
caratterizzata da diversi anelli a 5 termini.
Mn+ + EDTA4- ↔ M(EDTA)n-4
MEDTA  

n 4
Kf
M EDTA 
n
4
L’elevato valore delle costanti di formazione dei complessi EDTA-ione metallico è
indice della grande stabilità di questi complessi. Per comodità le Kf sono riportate
in forma logaritmica a causa dell’ampio range di valori in cui rientrano. Ad esempio
il complesso Ca2+ e EDTA4- ha una Kf = 1010.65 = 4.47 x 1010 a 25 °C, mentre la Kf per
il complesso tra Fe2+ e EDTA4- è pari a 1025.1 = 1.3 x 1025 a 25 °C
L’EDTA è oggi utilizzato
come additivo
alimentare, come agente
pulente, oppure nel
trattamento per
avvelenamento con
metalli pesanti per le sue
elevate capacità
chelanti.
Proprietà acido-base dell’EDTA
Tutti i potenziali siti di legame dell’EDTA possono agire da acidi e da basi deboli.
Sia i due atomi di azoto che i quattro gruppi carbossilici possono legare ioni metallici
solamente quando si trovano nella loro forma non protonata (coppie di elettronici
disponibili per la formazione dei legami di coordinazione). È per questa ragione che la
forma tetrabasica (EDTA)4- è indicata come la forma responsabile del legame con gli
ioni metallici.
Per determinare la forza con cui l’EDTA sarà in grado di complessare gli ioni metallici
di una soluzione, è necessario conoscere il pH della soluzione e la quantità di agente
chelante che in quelle condizioni è presente come (EDTA)4- .
Si deve usare lo stesso approccio degli acidi poliprotici per conoscere la frazione di
ciascuna forma di EDTA a diversi valori di pH.
Come si può vedere dal
grafico la forma EDTA4- è
presente solo a elevati
valori di pH.
La frazione di EDTA che
sarà presente all’equilibrio
come EDTA4-, può essere
calcolata nel seguente
modo (acidi poliprotici) :
αEDTA4- = Ka1 Ka2 Ka3 Ka4 Ka5 Ka6 / [H+]6 + Ka1[H+]5 + Ka1Ka2[H+]4 + Ka1Ka2Ka3[H+]3 + Ka1Ka2Ka3Ka4[H+]2
+ Ka1Ka2Ka3Ka4Ka5[H+] + Ka1Ka2Ka3Ka4Ka5Ka6
Questa equazione può essere utilizzata anche per calcolare direttamente la frazione di
EDTA4- ad un determinato valore di pH.
Effetto del pH sull’EDTA
Una nota bibite analcolica contiene EDTA
come agente chelante. Il pH è 3.22. Quale
sarà la frazione di EDTA presente
all’equilibrio sotto forma di EDTA4-? Quale
sarà la forma prevalente di EDTA a questo
pH?
Sostituendo nell’equazione:
αEDTA4- = Ka1 Ka2 Ka3 Ka4 Ka5 Ka6 / [H+]6 +
Ka1[H+]5 + Ka1Ka2[H+]4 + Ka1Ka2Ka3[H+]3 +
Ka1Ka2Ka3Ka4[H+]2 + Ka1Ka2Ka3Ka4Ka5[H+] +
Ka1Ka2Ka3Ka4Ka5Ka6
I valori di Kai di tabella 9.7 e
[H+] = 10-3,22 = 6,03 x 10-4 M
Si ricava αEDTA4- = 9,5 x 10-11
Questo risultato indica che a pH 3,22 meno
di 0.1 parti per miliardo di EDTA è presente
nella forma tetrabasica.
La forma prevalente è quella dibasica H2EDTA2-, che rappresenta circa il 77% dell’EDTA a questi
valori di pH (figura 9.7).
Trattamento delle reazioni collaterali
La costante di formazione o di stabilità condizionale (Kf ’) è una costante di equilibrio
che descrive la formazione di un complesso in determinate condizioni di reazione. Per
esempio, serve per studiare l’effetto del pH sulla capacità dell’EDTA (e altri leganti con
proprietà acido-base) di complessare uno ione metallico. In questo caso, sapendo che
solo la forma tetrabasica è in grado di legare in maniera apprezzabile uno ione
metallico, possiamo scrivere
αEDTA4- = [EDTA4-]/ CEDTA
ovvero
[EDTA4-] = αEDTA4- x CEDTA
sostituendo nell’equazione
MEDTA  

n 4
Kf
K'f  K f  EDTA4
M EDTA 
n
4
MEDTA  

n 4
M C
n
EDTA
Un vantaggio di utilizzare questa equazione è il fatto che essa rappresenta
un’espressione d’equilibrio basata sulla concentrazione totale di EDTA, un dato
solitamente noto.
Nel caso di Ni2+ e NH3
K a , NH
2
 NH  
dove
NiNH3  
K'f  K f  NH 3 
Ni C
3
2
NH 3
H  K

4
a , NH 4 
Previsione degli effetti di reazioni collaterali
L’equazione
K'f  K f  EDTA4
MEDTA  

n 4
M C
tiene conto dell’inflenza del pH, ma non di
n
EDTA
altre reazioni collaterali. Un esempio è la reazione di complessazione che si verifica a
valori elevati di pH tra il Ca2+ e ioni OH- (questo legante compete con l’EDTA a questi
valori di pH):
Ca2+ + OH- ↔ CaOH+
con Kf, CaOH+ = 2.0 x 101 eq.(1)
Un’altra possibile reazione collaterale è quella tra EDTA4-, Ca2+, e H+.
CaEDTA2- + H+
CaHEDTA-
Kf,CaHEDTA- = 1.3 x 103
eq.(2)
Per valutare l’effetto globale del pH su questi diversi processi si deve utilizzare una costante
condizionale. Per prendere in considerazione tutte queste reazioni, occorre scrivere
un’espressione di equilibrio per il legame tra EDTA4- e Ca2+:
C
CaEDTA   
x
Ca EDTA   C 
2
K f ,CaEDTA2
2
CaEDTA2
CaEDTA
4
Ca 2
Ca
EDTA4

CEDTA 
eq.(3)
αEDTA4- = [EDTA4-]/ CEDTA;
CCa = [Ca2+] + [CaOH-]; CCaEDTA = [CaEDTA2-] + [CaHEDTA-]
Queste espressioni di bilancio di massa possono a loro volta essere combinate con le espressioni
di equilibrio (1) e (2) per dare le formule di calcolo di αCa2+ e αCaEDTA2-, correlate alle
concentrazioni idrogenioniche e quindi al pH.
 Ca 
2
1

1  K CaOH  ([OH ])
eq.(4)
 CaEDTA 
2
1

1  K CaHEDTA ([ H ])
eq.(5)
L’eq (4) può essere ulteriormente semplificata sostituendo [OH-]=Kw/[H+].
Ora è possibile riscrivere l’eq.(3):
K ' f ,CaEDTA2  K f ,CaEDTA2
 EDTA  Ca
CCaEDTA
x

 CaEDTA
CCa CEDTA
4
2
eq.(6)
2
dove αEDTA4-, αCa2+ e αCaEDTA2- possono essere calcolati sulla base delle costanti di equilibrio delle
reazioni considerate e del pH (che consente di ricavare [H+]e [OH-]).
Tenendo conto degli effetti combinati di tutte queste reazioni, si può descrivere
dettagliatamente la dipendenza di K’f,CaEDTA2- dal pH. I risultati ottenuti sono descritti dalla figura
9.9.
MEDTA  

n 4
K'f  K f  EDTA
Da questo grafico di deduce che, tutto sommato, l’equazione

M n  C EDTA
dava una rappresentazione corretta del processo di
complessazione del calcio con l’EDTA in un ampio range di pH
Le differenze che si possono ravvisare con l’eq.(6), ottenuta attraverso un approccio più preciso,
sono:
1) Questa nuova curva mostra che a pH<4 sussiste un legame più forte di quello previsto con il
primo approccio. Questa è una conseguenza della reazione collaterale
CaEDTA2- + H+
CaHEDTA- che favorisce il legame fra Ca2+ e EDTA.
2) Il nuovo tracciato mostra che per pH>12 il legame è più debole rispetto a quello previsto dal
primo approccio. Questa deviazione è una conseguenza della formazione del complesso
Ca(OH)+ che impedisce al Ca2+ di legarsi all’EDTA.
4