Teoremi sui triangoli rettangoli File - TED

Triangoli rettangoli e funzioni goniometriche
pag.1 di 4
b  a  sen 
1
c  a  cos 
2
OP  1
b  c  tg 
3
PH  sen 
OH  cos 
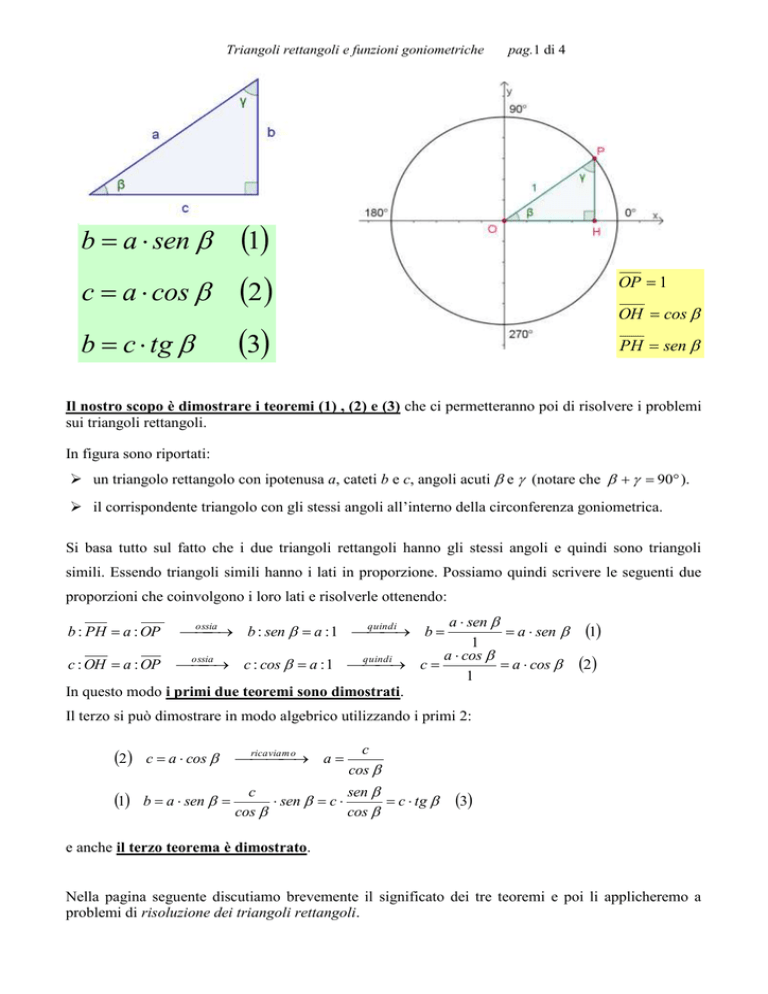
Il nostro scopo è dimostrare i teoremi (1) , (2) e (3) che ci permetteranno poi di risolvere i problemi
sui triangoli rettangoli.
In figura sono riportati:
 un triangolo rettangolo con ipotenusa a, cateti b e c, angoli acuti  e  (notare che     90 ).
 il corrispondente triangolo con gli stessi angoli all’interno della circonferenza goniometrica.
Si basa tutto sul fatto che i due triangoli rettangoli hanno gli stessi angoli e quindi sono triangoli
simili. Essendo triangoli simili hanno i lati in proporzione. Possiamo quindi scrivere le seguenti due
proporzioni che coinvolgono i loro lati e risolverle ottenendo:
a  sen 
 a  sen  1
1
a  cos 
c : OH  a : OP ossia

 c : cos   a : 1 quindi
 c 
 a  cos  2 
1
In questo modo i primi due teoremi sono dimostrati.
b : PH  a : OP
ossia

 b : sen   a : 1 quindi
 b 
Il terzo si può dimostrare in modo algebrico utilizzando i primi 2:
2
c  a  cos 
ricaviam
 o a 
1
b  a  sen  
sen 
c
 sen   c 
 c  tg 
cos 
cos 
c
cos 
3
e anche il terzo teorema è dimostrato.
Nella pagina seguente discutiamo brevemente il significato dei tre teoremi e poi li applicheremo a
problemi di risoluzione dei triangoli rettangoli.
Triangoli rettangoli e funzioni goniometriche
pag.2 di 4
b  a  sen 
1
c  a  cos 
2
b  c  tg 
3
I primi due teoremi coinvolgono cateto e ipotenusa e le funzioni seno o coseno:
1. CATETO = IPOTENUSA PER SENO DELL’ANGOLO OPPOSTO AL CATETO
2. CATETO = IPOTENUSA PER COSENO DELL’ANGOLO ADIACENTE AL CATETO
Il terzo teorema coinvolge i due cateti e la funzione tangente.
3. CATETO1 = CATETO2 PER TANGENTE DELL’ANGOLO OPPOSTO AL CATETO1
……………………………………………………………………………………………………………
Applicando le formule (1), (2), (3) e le relative formule inverse è possibile risolvere i problemi che
coinvolgono angoli e lati dei triangoli rettangoli. Vediamo alcuni esempi di problemi risolti.
1) Risolvere il triangolo rettangolo coi seguenti dati:
 ?
a ?
b  3  1   30


c?
a  ?

  ?
b  3 1
b
  30 
c ?
Conoscendo un cateto e il lato opposto possiamo utilizzare il teorema (1) per calcolare l’ipotenusa:
b
3 1
3 1
2
b  a  sen  ricavo
 a 


 3 1   2 3 1
1
sen  sen 30
1
2
Posso poi utilizzare il teorema (2) per calcolare l’altro cateto:
3
c  a  cos   2 3  1  cos 30  2  3  1 
 3 1  3  3  3
2










L’altro angolo acuto  si ricava invece come complementare dell’angolo  :
  90    90  30  60
E in questo modo il triangolo rettangolo è risolto.
……………………………………………………………………………………………………………
Triangoli rettangoli e funzioni goniometriche
2) Risolvere il triangolo rettangolo coi seguenti dati:
b  2 3 c  6


 ?
a  ?

  ?
a ?
pag.3 di 4
 ?
b2 3
  ?
c6
Conoscendo i due cateti possiamo utilizzare il teorema (3) per calcolare l’angolo  :
b 2 3
3


ricavo
   30
c
6
3
Posso poi utilizzare il teorema (1) per calcolare l’ipotenusa:
b
2 3
2 3
2
b  a  sen  ricavo
 a 


2 3 4 3
1
sen  sen 30
1
2
b  c  tg 
ricavo
 tg  
L’altro angolo acuto  si ricava invece come complementare dell’angolo  :
  90    90  30  60
E in questo modo il triangolo rettangolo è risolto.
……………………………………………………………………………………………………………
3) Risolvere il triangolo rettangolo coi seguenti dati:
b  7 a  25


  ? c  ?


  ?
a  25
 ?
b7
  ?
c ?
Conoscendo un cateto e l’ipotenusa possiamo utilizzare il teorema (1) per calcolare l’angolo  :
b 7
b  a  sen  ricavo
 sen   
a 25
Con l’aiuto della calcolatrice scientifica si può calcolare, approssimato, l’angolo  . Bisogna calcolare 7/25 e
poi applicare (usando il tasto di seconda funzione) la funzione inversa del seno al valore così calcolato.
 7
  16,26
 25 
L’altro angolo acuto  si ricava invece come complementare dell’angolo  :
  90    90  16,26  73,74
Si ottiene così:   sen 1 
Per calcolare in modo esatto l’altro cateto c bisogna però prima calcolare in modo esatto il coseno di  :
2
49
576 24
 7
cos    1  sen    1     1 


625
625 25
 25 
2
Posso poi utilizzare il teorema (2) per calcolare l’altro cateto:
24
c  a  cos   25 
 24
e il problema è risolto.
25
……………………………………………………………………………………………………………
Triangoli rettangoli e funzioni goniometriche
4) Risolvere il triangolo rettangolo coi seguenti dati:
pag.4 di 4
a ?
b  10   40

a  ? c  ?
  ?

 ?
b  10
  40 
c ?
Conoscendo un cateto e il lato opposto possiamo utilizzare il teorema (1) per calcolare l’ipotenusa:
b
10
10
b  a  sen  ricavo
 a 


 15,56
sen  sen 40 0,6428
Posso poi utilizzare il teorema (2) per calcolare l’altro cateto:
c  a  cos   15,56  cos 40  15,56  0,766  11,92
L’altro angolo acuto  si ricava invece come complementare dell’angolo  :
  90    90  40  50
Non essendoci angoli particolari i valori di a e c sono stati approssimati con l’uso della calcolatrice.
……………………………………………………………………………………………………………
5) Risolvere il triangolo rettangolo coi seguenti dati:
b  8 c  6

a  ?   ?
  ?

a ?
 ?
b8
  ?
c6
Conoscendo i due cateti possiamo utilizzare il teorema (3) per calcolare l’angolo  :
b 8 4
4
b  c  tg  ricavo
 tg    
ricavo
   tg 1    53,13
c 6 3
 3
Per calcolare in modo esatto l’ipotenusa bisogna però prima calcolare in modo esatto il coseno di  :
cos   
1
1  tg 2 

1
4
1  
 3
2

1
1
16
9

1
25
9

3
5
Posso poi utilizzare il teorema (2) per calcolare l’ipotenusa:
c
6
5
c  a  cos  ricavo
 a 

 6   10
cos   3 
3
 
 5
L’altro angolo acuto  si ricava invece come complementare dell’angolo  :
  90    90  53,13  36,87
E in questo modo il triangolo rettangolo è risolto.
……………………………………………………………………………………………………………