Document

Unità 2
Distribuzioni di probabilità
Misure di localizzazione
Misure di variabilità
Asimmetria e curtosi
1
DISTRIBUZIONI DI PROBABILITÀ
DISTRIBUZIONI DISCRETE DI PROBABILITÀ
Sia X una variabile casuale discreta e si supponga che i valori che
può assumere siano x1, x2, x3,…, valori che sono disposti in ordine
crescente. Si supponga inoltre che tali valori siano assunti con
probabilità
P(X=xk) = f(xk)
con k = 1,2,…
(1)
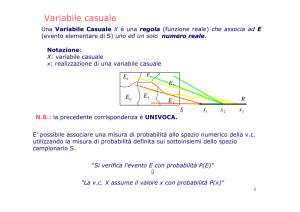
È conveniente introdurre la funzione di probabilità, anche nota
come distribuzione di probabilità, nel seguente modo:
P(X=x) = f(x)
(2)
Per x = xk l’eq. (2) coincide con l’eq. (1), mentre per tutti gli altri
valori di x si ha f(x) = 0.
2
In generale f(x) è una funzione di probabilità se:
a)
f(x)  0;
b)
 f (x)  1
x
La rappresentazione grafica di f(x) è detta grafico di
probabilità.
La f(x) può anche essere rappresentata graficamente mediante
un istogramma di probabilità (in questo caso la somma delle
aree è pari a 1).
3
ESEMPIO. Sia X la variabile casuale corrispondente al numero di
figli femmina in una famiglia con 2 figli. Si voglia trovare la
distribuzione di probabilità per X.
X può assumere i valori 0, 1 e 2. Supponendo identiche le
probabilità di nascita di un figlio maschio e femmina, la funzione
f(x) vale
0,25 per x  0
 0,5 per x  1

f (x)  
0,25 per x  2
 0
altrove
f (x)
f (x)
0,5
0,5
0,25
0,25
0
1
2
Grafico di probabilità
x
-1
0
1
2
x
Istogramma di probabilità
4
DISTRIBUZIONI CONTINUE DI PROBABILITÀ
Se X è una variabile continua la probabilità che X assuma un
valore particolare è di solito zero e quindi non si può definire una
funzione di probabilità in modo simile a quanto fatto per una
variabile casuale discreta.
Tuttavia anche in questo caso è sensato parlare della probabilità
che X sia compresa fra due diversi valori. Ciò suggerisce di
postulare l’esistenza di una funzione f(x) che, in analogia alla
funzione di probabilità per variabili discrete, rispetta i vincoli:
a)
f(x)  0;

b)
 f (x )  1

N.B. La seconda equazione è la formulazione matematica del
fatto che la variabile casuale X deve assumere un valore
compreso fra – e +.
5
La probabilità che X cada all’interno dell’intervallo (a,b) sarà allora
definita come:
b
P (a  X  b)   f ( x ) dx
(3)
a
b
(Si ricorda che
 f ( x ) dx
rappresenta, dal punto di vista
a
geometrico, l’area che compresa fra la curva f(x) e l’asse x, fra i
punti a e b).
Una funzione f(x) che soddisfi le condizioni poste è una funzione
di probabilità di una variabile casuale continua. Più comunemente
è detta funzione densità di probabilità o, semplicemente,
densità di probabilità.
6
La funzione densità di probabilità più nota è quella relativa agli
errori di misura.
Se si esegue una serie molto grande di misure di una grandezza
relativa a un determinato oggetto, si otterranno valori diversi e ciò
è dovuto agli errori di misura (differenza fra il valore vero e quello
misurato), che definiscono una variabile casuale continua. Tale
variabile ha una curva di densità di probabilità simmetrica,
qualitativamente simile a una campana, che prende il nome di
distribuzione normale o distribuzione gaussiana.
Matematicamente essa è espressa dalla relazione
( x   )2

2
1
(4)
2

f (x) 
e
   x  
 2
dove  e  sono i parametri che caratterizzano questa
distribuzione.
La distribuzione normale assume una notevole importanza anche in
medicina, poiché varie variabili biomediche possono essere
considerate di tipo gaussiano.
7
COME RIASSUMERE I DATI
Data una variabile casuale X, si possono definire alcune misure
che danno informazioni importanti circa la sua distribuzione di
probabilità.
Le più usate sono:

misure di tendenza centrale,

misure di dispersione

misure di asimmetria

misure di curtosi,

momenti.
In particolare le misure di tendenza centrale e quelle di
dispersione danno rispettivamente informazioni circa la
localizzazione e la variabilità associate alla variabile casuale
oggetto di studio.
8
Se una funzione densità di
probabilità ha “una coda più
lunga a destra del massimo
centrale”, la distribuzione si dice
positivamente asimmetrica.
Asim m etria positiva o destra
12
10
frequenz a
L’asimmetria
(in
inglese
skewness) è un valore che
fornisce una misura della
mancanza di simmetria della
distribuzione in esame.
8
6
4
2
0
0
20
40
60
80
valori
100
120
140
160
media=63,65
moda = 48
mediana =58
Nel caso opposto la distribuzione è negativamente asimmetrica.
Esistono diversi indici di asimmetria. Per ognuno di essi il valore 0
fornisce una condizione necessaria, ma non sufficiente, affinché
una distribuzione sia simmetrica. (Ogni distribuzione simmetrica
ha indice 0, ma esistono anche distribuzioni non simmetriche con
indice 0).
9
La curtosi (kurtosis) dà una misura del grado di altezza
raggiunto dalla distribuzione in esame, generalmente in relazione
alla distribuzione normale.
Il calcolo dei momenti (di vario ordine) consente in generale di
caratterizzare più precisamente la distribuzione in esame.
La definizione ed il calcolo di queste misure, a partire dalla
conoscenza della distribuzione in esame, può richiedere una
buona preparazione matematica relativa al calcolo integrale e
quindi, per semplicità, tale problema non verrà affrontato in
maniera esaustiva in questa sede.
Di seguito ci limiteremo a definire, in maniera semplice, le
principali misure di tendenza centrale (localizzazione) e di
dispersione (variabilità).
10
MISURE DI TENDENZA CENTRALE
Si supponga di osservare tutti gli elementi relativi ad una
popolazione (ad esempio la popolazione dei bambini italiani di 10
anni di età) e di voler studiare una variabile casuale X (ad
esempio la statura) di questa popolazione.
Per avere un’informazione quantitativa circa la posizione
occupata dalla variabile in studio sulla scala delle stature, si può
utilizzare una misura, detta valore medio della popolazione (o,
più semplicemente, media della popolazione).
Il valore medio della popolazione si chiama spesso valore atteso
o speranza matematica.
11
Il valore medio della variabile X nella popolazione è generalmente
rappresentato con il simbolo E(x) [expected value] o con la lettera
greca  e, nel caso particolare di distribuzioni discrete di
probabilità, è semplicemente definito come
E ( X )     f (x)  x
x
dove f(x) è la distribuzione di probabilità della variabile discreta X.
Se la variabile casuale X è continua il calcolo del valore medio
richiede l’uso dell’operatore integrale, in particolare
E( X )   

 f ( x )  x dx

12
N.B. Il valore medio è un un indice di localizzazione, poiché
fornisce un’informazione circa la posizione occupata dalla
variabile casuale X sulla scala di misura.
Altre misure di tendenza centrale sono:

la mediana,

la moda.
La mediana è quel valore ξ per cui P(X  ξ ) = P(X  ξ ) = 0,5.
Nel caso di una distribuzione continua, la mediana corrisponde
all’ascissa che spezza la curva di densità di probabilità in due
parti a cui corrisponde un’area sottesa pari a 0,5.
È detta moda quel valore di X a cui corrisponde un massimo della
distribuzione di probabilità.
Una distribuzione può avere più di una moda (distribuzione
bimodale, trimodale o multimodale).
13
MISURE DI DISPERSIONE
Una misura di dispersione di una variabile casuale X
comunemente impiegata è la varianza e viene di solito
rappresentata con il simbolo  2.
È definita come il valore medio degli scarti quadratici dalla media
 , cioè:
 2 = Var(X) = E [(x – )2]
La varianza è quindi un numero non negativo.
La radice quadrata positiva della varianza è detta deviazione
standard (), cioè:
  E [( x   )2 ]
14
La varianza e la deviazione standard sono entrambi misure di
variabilità dei valori della variabile casuale X attorno al suo valore
medio .
↓
Se i valori di X sono concentrati vicino al valore medio, sia la
varianza sia la deviazione standard sono piccole, mentre esse
crescono quando i valori sono dispersi lontano dal valore medio.
Può essere utile descrivere la variabilità in percentuale rispetto al
valore medio, ottenendo così il coefficiente di variazione (CV)
CV ( X ) 

 100

N.B. CV è adimensionale
ESERCIZIO: Sia X la variabile casuale corrispondente al numero
di figli femmina in una famiglia con 2 figli. Si calcoli il valore
medio, la deviazione standard ed il coefficiente di variazione di X.
15
Una diversa misura di dispersione è il campo interquartile.
Per definire questa misura è necessario introdurre prima il
concetto di percentile:
data una variabile casuale X si definisce K-esimo percentile quel
valore x tale che
P(X  x) = K
e
P(X  x) = 100–K.
La mediana corrisponde quindi al 50° percentile ed è spesso
chiamata secondo quartile ed indicata con Q2.
Il 25° e il 75° percentile sono analogamente detti primo quartile
(Q1) e terzo quartile (Q3).
16
L’intervallo di valori compreso fra Q1 e Q3 è detto intervallo
interquartile.
N.B. L'intervallo interquartile contiene la metà della popolazione,
indipendentemente dalla forma della distribuzione della variabile.
La differenza Q3 – Q1 è detta campo interquartile e la sua metà
campo semi-interquartile.
Entrambi queste misure rappresentano indici di dispersione.
17
ALCUNE CONSIDERAZIONI SULLA DISTRIBUZIONE GAUSSIANA
Si noti che  e  sono i soli due parametri che compaiono
nell’espressione matematica che definisce la distribuzione gaussiana.
In altre parole la densità di probabilità di una variabile casuale X di tipo
gaussiano è completamente definita se si conoscono il valore medio e
la deviazione standard della popolazione.
Di conseguenza, in questo caso particolare, tali indici non
costituiscono solo importanti elementi informativi circa la variabile in
studio, ma forniscono anche tutti gli elementi necessari per una
completa descrizione della popolazione.
Ciò non è però generalmente valido se la variabile casuale X ha una
distribuzione diversa da quella di Gauss. In questi casi può essere
preferibile utilizzare altri indici di tendenza centrale e di dispersione
maggiormente informativi. In pratica, quale indice di tendenza centrale
conviene utilizzare la mediana e come indice di dispersione il campo
interquartile o il campo semi-interquartile.
18