Intelligenza Artificiale
Reti Neurali
Stefano Cagnoni
Reti Neurali Artificiali
Paradigma computazionale caratterizzato dal massiccio
parallelismo di processori elementari (neuroni artificiali).
Ispirato da un modello
(McCulloch & Pitts 1943).
matematico
del
neurone
Ogni processore può eseguire funzioni di per sé poco
significative, ma l’azione combinata di un numero elevato
di unità può realizzare funzioni anche molto complesse.
Nate alla fine degli anni ‘50, presto abbandonate per i
limiti evidenziati da Minsky (Perceptrons, 1969), per poi
riaffermarsi alla fine degli anni ‘80, quando fu dimostrato
che tali limiti potevano essere superati.
Neurone artificiale
Costituito da due stadi:
•sommatore lineare (produce il cosiddetto net input)
•funzione di attivazione non lineare tipicamente a soglia;
gradino o sigmoide 1 / (1 + e -(x -q))
Rete Neurale Artificiale
Architettura a più strati:
• strato di ingresso
• strato/i nascosto/i
• strato di uscita
IN
OUT
Reti feedforward:
connessioni possibili solo
in avanti
Reti ricorrenti:
connessioni possibili
anche da strati più vicini
alle uscite (all’indietro)
Reti Neurali Artificiali
Ad ogni connessione è associato un peso, utilizzato nel
sommatore che costituisce il primo stadio del neurone che
riceve dati attraverso la connessione.
Il comportamento di una rete neurale è quindi determinato:
• dal numero dei neuroni
• dalla topologia
• dai valori dei pesi associati alle connessioni
Problemi risolubili con diverse topologie
Reti Neurali Artificiali
Proprietà:
• Capacità di apprendere da esempi
• Capacità di generalizzare
• Capacità di astrarre
• Insensibilità al rumore
• Decadimento graduale delle prestazioni
Training
L’addestramento (training) di una rete neurale è un processo
iterativo che modifica i pesi della rete sulla base delle
‘prestazioni’ della rete su un insieme di esempi, al fine di
minimizzare una funzione obiettivo (cioè di raggiungere un
comportamento desiderato).
L’insieme degli esempi su cui la rete viene addestrata è detto
training set
Le prestazioni della rete, ottimizzate sul training set, devono
essere poi verificate su dati che non appartengono al training
set (test set)
Training
L’addestramento può essere di 2 tipi:
• Con supervisione: gli esempi sono divisi in una parte che
contiene dati di ingresso ed un’altra parte (teaching input) che
contiene le uscite che si desidera ottenere in corrispondenza
di tali ingressi.
I pesi sono adattati in modo da minimizzare le differenza fra il
comportamento della rete e quello desiderato.
• Senza supervisione: gli esempi sono costituiti dai soli dati di
ingresso.
I pesi vengono adattati in modo tale che la rete si autoorganizzi in modo da riflettere alcune caratteristiche del
training set.
Training
Addestramento con supervisione:
Backpropagation
Metodo di ottimizzazione basato sul principio della
discesa lungo il gradiente.
Minimizza una funzione ‘errore quadratico’
S t=1,T S i=1,N (y(t) - d(t))2 / 2
N=dim. Uscita, T=n.esempi, y(t)=output rete, d(t)=teaching input
Applicabile a reti di tipo feedforward (in cui è possibile
definire un ordine temporale nell’attivazione dei neuroni)
Deriva il nome dal fatto che la modifica dei pesi avviene
sulla base della “propagazione all’indietro” dell’errore
dallo strato di uscita verso quello di ingresso.
Addestramento con supervisione:
Backpropagation
• Si inizializzano i pesi con piccoli numeri random
Ad ogni iterazione
Per ogni esempio nel training set:
•si calcola l’uscita prodotta dalla attuale
configurazione della rete
•si calcola l’errore
•si modificano i pesi ‘spostandoli’ lungo il
gradiente della funzione errore calcolato
rispetto ai pesi
fino al raggiungimento di un limite inferiore prestabilito per
l’errore o di un certo numero prestabilito di iterazioni
Regola di derivazione a catena
+x/ zi = x/ zi + S j>i +x/ zj * zj/ zi
Un esempio:
z2 = 4 * z1
z3 = 3 * z1 + 5 * z2
z3/ z1 = 3, ma in realtà z3 dipende da z1 anche tramite
z2
+z3/ z1 = 23 che dà la vera dipendenza, propagata
attraverso le variabili intermedie, di z3
da z1
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
Modello biologico di partenza
Nella corteccia cerebrale esistono mappature (proiezioni) di
stimoli sensoriali su specifiche reti di neuroni corticali.
I neuroni senso-motori costituiscono una mappa distorta
(l’estensione di ciascuna regione è proporzionale alla
sensibilità della corrispondente area corporea, non alle
dimensioni) della superficie corporea.
Tuttavia, parti adiacenti della corteccia corrispondono a parti
adiacenti della superficie corporea.
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
Interazioni laterali fra neuroni
• eccitazione laterale a breve raggio (50-100 mm)
• azione inibitoria (fino a 200-500 mm)
• azione eccitatoria debole a lungo raggio (fino a qualche cm)
approssimabili come:
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
Mappe “sensoriali”, costituite da un singolo strato di neuroni
in cui le unità si specializzano a rispondere a stimoli diversi
in modo tale che:
• ingressi di tipo diverso attivino unità diverse
• unità topologicamente vicine vengano attivate da ingressi
simili
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
•Singolo strato di neuroni ni i=1,w*h (w=largh. h= alt. mappa)
•Ogni ingresso X={xj, j=1,N} è collegato a tutti i neuroni
•Ogni connessione è associata ad un peso wij
•Funzione di attivazione
fi= 1/d(Wi,X) d= distanza
•Presenza di interazioni laterali
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
I pesi di ciascun neurone vengono modificati:
•in senso eccitatorio proporzionalmente al valore della
propria funzione di attivazione e di quelle dei neuroni
appartenenti ad un loro vicinato, proporzionalmente alla
distanza da essi;
•in senso inibitorio proporzionalmente al valore della
funzione di attivazione dei neuroni esterni al vicinato,
proporzionalmente alla distanza da essi.
Quindi, se si ripropone lo stesso ingresso alla rete:
•i neuroni che avevano un valore elevato di attivazione e i
vicini mostreranno un’attivazione ancora maggiore
•i neuroni che rispondevano poco risponderanno ancor meno
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
Se si presentano dati ben distribuiti nello spazio degli
ingressi, in modo iterativo, ogni neurone si specializza a
rispondere a dati di un certo tipo
Inoltre, neuroni vicini rispondono a stimoli vicini proiettando,
in pratica, lo spazio degli ingressi sullo strato di neuroni.
Risultati:
•riduzione di dimensionalità dei dati da N (dim. dell’ingresso)
a m (dimensione della mappa);
•ogni dato è rappresentato dalla coordinata dell’unità su cui
si proietta, cioè quella che ha massima attivazione, cioè
quella per cui i cui pesi sono più simili (vicini) al dato stesso.
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
In pratica:
•si partiziona lo spazio degli ingressi in tanti sottospazi quanti
sono i neuroni
•ogni sottospazio si di S={Xk} è definito come:
si = {Xj t.che d(Xj,Wi) = mint (Xi,Wt) }
Tassellazione di Voronoi
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
Semplificazioni del modello per implementazione algoritmo di
addestramento:
•si modificano i pesi solo nell’intorno del neurone che ha max
attivazione (neurone vincente, questo tipo di addestramento è
detto anche competitive learning)
•si considerano solo le interazioni laterali eccitatorie all’interno
di un intorno limitato del neurone vincente
NB Modificare i pesi in senso eccitatorio significa renderli più
simili all’ingresso; modificarli in senso inibitorio significa renderli
meno simili.
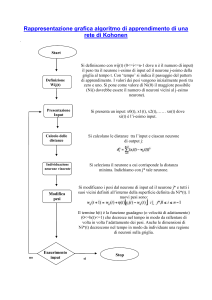
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
a=C
(a = learning rate, C costante positiva piccola << 1)
Ripeti
- Per ogni esempio xi nel training set:
•determina l’unità vincente nw
•modifica i pesi dell’unità vincente e di quelle che si
trovano in un suo intorno nel modo seguente:
wj(t+1) = wj (t) + a (xi - wj (t))
- a(k+1) = a(k) * (1 - g)
(g costante positiva piccola << 1 )
finché la rete non raggiunge una configurazione stabile
Addestramento senza supervisione:
Mappe auto-organizzanti (SOM) di Kohonen
Realizzazione di un clustering dei dati, cioè di una
identificazione, nello spazio degli ingressi, di partizioni indotte
dalle similitudini/differenze fra i dati
•ogni partizione è rappresentata da un prototipo (centroide)
definito dal valore dei pesi del neurone corrispondente
•il clustering è di tipo non supervisionato, in quanto non
abbiamo alcuna informazione a priori sulle classi di
appartenenza dei dati
•a posteriori è possibile etichettare (classificare) dati in base
alla partizione dello spazio degli ingressi cui appartengono