Reti Neurali
Generalità
Reti Neurali Biologiche
Neurone
• Circa 1011 nell’uomo, di oltre 100 tipi diversi, con oltre
1014 connessioni
• All’attivazione (stimoli ricevuti attraverso i dendriti >
soglia) gli impulsi generati dall’eccitazione del soma si
propagano attraverso l’assone verso gli altri neuroni.
Dendriti
Nucleo
Corpo cellulare
(soma)
Assone
Reti Neurali Biologiche
Neurone
• I punti di contatto fra neuroni si chiamano sinapsi e
possono essere di tipo inibitorio o eccitatorio
• A livello di sinapsi le terminazioni dei 2 neuroni sono
separati da un’intercapedine attraverso cui avviene la
trasmissione del treno di impulsi per via elettrochimica
(emissione di una sostanza detta mediatore sinaptico)
• Frequenza massima degli impulsi <= 1KHz, quindi
trasmissione dell’informazione piuttosto lenta
• Ipotesi di trasmissione distribuita e parallela
dell’informazione
Reti Neurali Artificiali: cenni storici
•Paradigma computazionale ispirato da un modello
matematico del neurone (McCulloch & Pitts 1943) realizzato
per studiare le capacità computazionali del neurone e delle
reti neurali biologiche.
•Hebb (1949) propone un modello di apprendimento ‘sinaptico’
(legge di Hebb)
•Rosenblatt (1957) definisce il percettrone e un algoritmo di
apprendimento, con cui dimostra la possibilità di riconoscere
forme e risolvere altri problemi.
•Alla fine anni ‘60 abbandono dela ricerca per i limiti
evidenziati da Minsky (Perceptrons, 1969): non erano in grado
di imparare lo XOR.
•Riaffermazione alla fine degli anni ‘80 (Rumelhart et al.,
Grossberg, Hopfield).
Neurone artificiale
Costituito da due stadi:
•sommatore lineare (produce il cosiddetto net input)
net = Sj wj ij
•funzione di
o = f (net)
attivazione
f
non
lineare
a
soglia
Neurone artificiale
Possibili funzioni di attivazione:
o=
o=
1
se (x - q) > 0
0
se (x - q) < 0
+1
se (x - q) > 0
-1
se (x - q) < 0
Gradino
Gradino bipolare
o=
1 / (1 + e -(x -q))
Sigmoide
o=
tanh (x - q)
Tangente iperbolica
q è una costante (bias) che ha il ruolo di soglia.
Può essere inglobato nel net aggiungendo una connessione
con ingresso costante uguale ad 1 e peso associato uguale al
bias.
Rete Neurale Artificiale
Architettura a più strati:
• strato di ingresso
• strato/i nascosto/i
• strato di uscita
IN
OUT
Reti Neurali Artificiali
Ad ogni connessione è associato un peso, utilizzato nel
sommatore che costituisce il primo stadio del neurone che
riceve dati attraverso la connessione.
Il comportamento di una rete neurale è quindi determinato:
• dal numero dei neuroni
• dalla topologia
• dai valori dei pesi associati alle connessioni
Rete Neurale Artificiale: classificazione
•Sulla base del flusso dei segnali
•Reti feedforward: connessioni possibili solo in avanti
•Reti ricorrenti: connessioni possibili anche da strati più vicini alle
uscite (all’indietro)
•Sulla base dell’organizzazione delle connessioni
•Reti totalmente connesse : ogni neurone è connesso con ogni altro
•Reti parzialmente connesse : ogni neurone è connesso ad un
particolare sottoinsieme di neuroni
•reti singolo strato : le unità di ingresso sono connesse
direttamente a quelle di uscita
•reti multistrato : organizzate in gruppi topologicamente
equivalenti (strati)
Rete Neurale Artificiale: computabilità
Teorema di Kolmogorov:
Qualsiasi funzione continua y=f(x):Rn->Rm può essere computata da una
opportuna rete ricorrente a 3 strati avente n unità nello strato di ingresso,
2n+1 nello strato nascosto ed m nello strato di uscita e totalmente
connessa fra gli strati
Problemi :
• Teorema che dimostra la sola esistenza della soluzione
• Le unità considerate nel teorema hanno caratteristiche diverse dai
neuroni artificiali utilizzati nelle reti neurali
Altri teoremi di esistenza (sulle reti neurali multistrato):
Una rete neurale con uno strato nascosto avente un numero sufficiente di
unità può approssimare qualsiasi funzione continua
Problemi risolubili con diverse topologie
Reti Neurali Artificiali
Proprietà:
• Capacità di apprendere da esempi
• Capacità di generalizzare (risposte simili in corrispondenza di
esempi simili a quelli su cui sono state addestrate)
• Capacità di astrarre (risposte corrette in corrispondenza di
esempi diversi da quelli su cui sono state addestrate)
• Insensibilità al rumore (capacità di generalizzare anche in
presenza di dati alterati o incerti)
• Decadimento graduale delle prestazioni (il comportamento si
altera gradualmente se si eliminano connessioni o si alterano i pesi)
Training
L’apprendimento (da esempi) da parte di una rete neurale si
configura come un processo iterativo di ottimizzazione:
• i pesi della rete vengono modificati sulla base delle
‘prestazioni’ della rete su un insieme di esempi
• si minimizza una funzione obiettivo che rappresenta di
quanto il comportamento della rete si discosta da quello
desiderato
L’insieme degli esempi su cui la rete viene addestrata è detto
training set
Le prestazioni della rete devono essere verificate su un
insieme di dati (test set) che non appartengono al training set
Training
L’apprendimento può essere di 2 tipi:
con supervisione
(supervised learning)
senza supervisione
(unsupervised learning)
• Con supervisione: esempi divisi in due componenti:
• pattern di ingresso
• teaching input, che specifica l’output che si desidera
ottenere in corrispondenza di tale pattern
I pesi sono adattati in modo da minimizzare le differenze fra il
comportamento della rete e quello desiderato.
Training
Senza supervisione: esempi costituiti da soli dati di ingresso.
• pesi adattati in modo tale che la rete si auto-organizzi in
modo da riflettere alcune caratteristiche e regolarità del
training set
• si parla anche di regularity discovery o feature detection
Training
Reti Neurali
Apprendimento supervisionato
Addestramento con supervisione:
Legge di Hebb
• Prima proposta di modello di apprendimento
• Modello di tipo correlazionale nato per giustificare
l’apprendimento nelle reti neuronali biologiche
• “se due unità sono attive nello stesso istante il peso
della relativa connessione deve essere incrementato”
Dwij = e oioj
e = Learning Rate
• Problemi:
- non sempre conduce a risultati corretti
- continuando a mostrare gli stessi esempi i pesi
crescono indefinitamente (non è plausibile
biologicamente e porta a fenomeni di saturazione)
Addestramento con supervisione:
Legge di Hebb
Se si considera una rete singolo strato con attivazioni
lineari e ingressi reali l’apprendimento hebbiano funziona
solo se i vettori di ingresso formano un insieme
ortogonale.
Quindi, se lo spazio di ingresso ha dimensione N, si
possono apprendere al max N associazioni esatte
In ogni caso la legge è importante in quanto:
• troviamo traccia dei suoi principi anche in regole di
apprendimento più potenti
• è un utile termine di paragone nello studio delle regole
di apprendimento
Addestramento con supervisione:
Percettroni
• Prima realizzazione di
(Rosenblatt, fine anni ‘50)
rete
neurale
artificiale
• Studiato inizialmente per problemi di riconoscimento
forme da stimoli di tipo visivo
• Strato di ingresso (retina) cui sono collegate unità che
realizzano una funzione f binaria dell’ingresso (stimolo
visivo) collegati poi ad un neurone con attivazione a
soglia.
f1
f2
fn
w1
w2
wn
S
o
q
Addestramento con supervisione:
Percettroni
Possono realizzare funzioni estremamente complicate
(ad es. distinzione fra figure concave e convesse)
Per il percettrone esiste una legge di apprendimento:
1. si presenta un pattern di ingresso e si calcola l’uscita
2. se il pattern è stato classificato in modo corretto, ripeti
1. con un nuovo pattern
3. se l’uscita è alta e il teaching input è 0, decrementa di
uno i pesi delle linee per cui ii=1 e incrementa la
soglia di uno
4. se l’uscita è bassa e il teaching input è1 fa l’inverso
(incrementa i pesi e decrementa la soglia)
5. si ripetono i passi precedenti finché i pesi non
convergono.
Addestramento con supervisione:
Percettroni
Formalmente:
op = 1 se net = Si wi ipi > q
0 altrimenti
Dpwi = (tp - op) ipi
Dp q = (op - tp)
In base a un teorema (Rosenblatt) converge alla
soluzione in un numero finito di passi, se la soluzione
esiste
Purtroppo, non sempre esiste (es. XOR, se le uscite
della funzione non sono linearmente separabili)
Addestramento con supervisione:
discesa lungo il gradiente
• Si inizializzano i pesi
Ad ogni iterazione
Per ogni esempio nel training set:
•si calcola l’uscita prodotta dalla attuale
configurazione della rete
•si calcola l’errore
•si modificano i pesi ‘spostandoli’ lungo il
gradiente della funzione errore calcolato
rispetto ai pesi
fino al raggiungimento di un limite inferiore prestabilito per
l’errore o di un certo numero prestabilito di iterazioni
Addestramento con supervisione:
Regola Delta (o di Widrow e Hoff)
Data una rete monostrato con attivazioni lineari, un training set
T = { (xp, tp) : p = 1, …., P}
e una funzione ‘errore quadratico’ sul pattern p-mo
Ep = S j =1,N (tpj -opj)2 / 2
N=n.unità di uscita, opj,tpj= output/teaching input per l’unità j
e una funzione ‘errore globale’
E = S p = 1,P Ep
P=n.esempi
E = E(W), W = matrice dei pesi wij associati alle connessioni ij
(dall’unità i verso l’unità j)
Se vogliamo minimizzare E possiamo utilizzare una discesa lungo il
gradiente, che converge al minimo locale di E più vicino al punto di
partenza (inizializzazione dei pesi)
Addestramento con supervisione:
Regola Delta
Il gradiente di E ha componenti
E/wij = Sp Ep/wij
Per la regola di derivazione delle funzioni composte
Ep/wij = Ep/opj · opj/wij
Dalla definizione di errore
- Ep/opj = (tpj - opj) = dpj
(errore commesso dall’unità j sul pattern p)
Per la linearità delle unità
(opj = Si wij ipi)
opj/wij = ipi
da cui
Ep/wij = - dpj ipi
e quindi
E/wij = - Sp dpj ipi
Addestramento con supervisione:
Regola Delta
Discesa lungo il gradiente:
Dwij = - e E/wij = Sp e Ep/wij = e Sp dpj ipi = Sp Dpwij
Quindi, se e è sufficientemente piccolo, possiamo
modificare i pesi dopo la presentazione di un singolo
pattern secondo la regola
Dpwij = e dpj ipi
NB Sono tutte quantità facilmente calcolabili
Addestramento con supervisione:
Regola Delta Generalizzata (Backpropagation)
La regola delta è applicabile solo ad un caso particolare
di reti (singolo strato con funzione di attivazione lineare)
E’ possibile generalizzare la regola delta per
configurazioni multi-strato della rete e per funzioni di
attivazione non lineari.
Le reti devono essere di tipo feedforward (è possibile
definire un ordine topologico dei neuroni e quindi
temporale nell’attivazione dei neuroni)
Le funzioni di attivazione fj(netj) devono essere continue,
derivabili e non decrescenti
netpj= Si wij opi per una rete multistrato
Addestramento con supervisione:
Regola Delta Generalizzata (Backpropagation)
Anche in questo caso si usa la discesa lungo il gradiente
Dpwij = - e Ep/wij
Per la proprietà di derivazione delle funzioni composte
Ep/wij = Ep/netpj · netpj/wij
netpj/wij = /wij Sk wkj opk = opi
Definiamo: dpj = - Ep/netpj (stessa definizione data per la regola
delta.Infatti per le reti considerate opj=netpj )
ottenendo così:
Ep/wij = e dpj opi (analogo della regola delta)
Resta da calcolare dpj
Addestramento con supervisione:
Regola Delta Generalizzata (Backpropagation)
dpj = - Ep/netpj = - Ep/opj · opj/netpj
Ma opj = fj(netpj)
e
opj/netpj = dopj/dnetpj = f’j(netpj)
Se uj è una unità di uscita
Ep/opj = - (tpj - opj)
Quindi per tali unità
dpj = - (tpj - opj) f’j(netpj)
Addestramento con supervisione:
Regola Delta Generalizzata (Backpropagation)
Se invece uj è una unità nascosta
Ep/opj = Sk Ep/netpk · netpk/opj =
= Sk Ep/netpk · /opj Si wik opi =
= Sk Ep/netpk · wjk = Sk dpk wjk
Quindi, per le unità nascoste, si avrà
dpj = f’j(netpj) · Sk dpk wjk
Quindi per le unità nascoste l’errore dpj è calcolato
ricorsivamente a partire dalle unità di uscita (error
backpropagation)
Addestramento con supervisione:
Regola Delta Generalizzata (Backpropagation)
Riassumendo:
1. Si inizializzano i pesi
2. Si presenta il pattern pmo
• si calcolano le uscite opj corrispondenti
• si calcola l’errore per le unità di uscita
dpj = - (tpj - opj) f’j(netpj)
• Per le unità nascoste si applica ricorsivamente
dpj = f’j(netpj) · Sk dpk wjk
a partire dallo strato nascosto più vicino all’uscita
3. Si apportano le modifiche ai pesi
Dpwij = e dpj opj
4. Si ripetono i punti 2. e 3. fino a convergenza
Addestramento con supervisione:
Regola Delta Generalizzata (Backpropagation)
Rigorosamente si dovrebbe applicare la variazione dopo
avere esaminato tutti i pattern (addestramento batch),
ma se e è piccolo si ottiene lo stesso risultato
modificandoli dopo ogni pattern (addestramento online).
Se si inizializzano i pesi a 0 problemi di convergenza,
quindi di solito si usano valori piccoli e diversi (0.05-0.1)
Per scendere davvero lungo il gradiente e dovrebbe
essere infinitesimo, ma più piccolo è e più lenta è la
convergenza. Ma se e è troppo grande potremmo
‘sorvolare’ un minimo. Si può usare un learning rate
adattativo.
La discesa lungo il gradiente è poco efficiente.
Regola delta per reti multistrato (feedforward):
regola di derivazione a catena
+x/ zi = x/ zi + S j>i +x/ zj * zj/ zi
Un esempio:
z2 = 4 * z1
z3 = 3 * z1 + 5 * z2
z3/ z1 = 3, ma in realtà z3 dipende da z1 anche tramite
z2
+z3/ z1 = 23 che dà la vera dipendenza, propagata
attraverso le variabili intermedie, di z3
da z1
Reti Neurali
Apprendimento non supervisionato
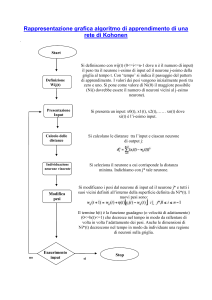
Reti di Kohonen
Mappe auto-organizzanti (SOM) di Kohonen
Homunculus
Modello biologico di partenza
Nella corteccia cerebrale esistono mappature
(proiezioni) di stimoli sensoriali su specifiche
reti di neuroni corticali.
I neuroni senso-motori costituiscono una
mappa distorta (l’estensione di ciascuna
regione è proporzionale alla sensibilità della
corrispondente area corporea, non alle
dimensioni) della superficie corporea.
Tuttavia, parti adiacenti della corteccia
corrispondono a parti adiacenti della
superficie corporea.
Mappe auto-organizzanti (SOM) di Kohonen
Interazioni laterali fra neuroni
• eccitazione laterale a breve raggio (50-100 mm)
• azione inibitoria (fino a 200-500 mm)
• azione eccitatoria debole a lungo raggio (fino a qualche cm)
approssimabili come:
Mappe auto-organizzanti (SOM) di Kohonen
Mappe “sensoriali”, costituite da un singolo strato di neuroni
in cui le unità si specializzano a rispondere a stimoli diversi
in modo tale che:
• ingressi di tipo diverso attivino unità diverse
• unità topologicamente vicine vengano attivate da ingressi
simili
Mappe auto-organizzanti (SOM) di Kohonen
•Singolo strato di neuroni ni i=1,w*h (w=largh. h= alt. mappa)
•Ogni ingresso X={xj, j=1,N} è collegato a tutti i neuroni (quindi
ad ogni neurone afferiscono N connessioni)
•Ogni connessione è associata ad un peso wij
•Funzione di attivazione
fi 1/d(Wi,X) d= distanza
•Presenza di interazioni laterali
Mappe auto-organizzanti (SOM) di Kohonen
I pesi di ciascun neurone vengono modificati:
•in senso eccitatorio proporzionalmente al valore della
propria funzione di attivazione e di quelle dei neuroni
appartenenti ad un loro vicinato, in funzione della distanza
da essi;
•in senso inibitorio proporzionalmente al valore della
funzione di attivazione dei neuroni esterni al vicinato, in
funzione della distanza da essi.
Quindi, se si ripropone lo stesso ingresso alla rete:
•i neuroni che avevano un valore elevato di attivazione e i
vicini mostreranno un’attivazione ancora maggiore
•i neuroni che rispondevano poco risponderanno ancor meno
Mappe auto-organizzanti (SOM) di Kohonen
Se si presentano dati ben distribuiti nello spazio degli
ingressi, in modo iterativo, ogni neurone si specializza a
rispondere a dati di un certo tipo
Inoltre, neuroni vicini rispondono a stimoli vicini proiettando,
in pratica, lo spazio degli ingressi sullo strato di neuroni.
Risultati:
•riduzione di dimensionalità dei dati da N (dim. dell’ingresso)
a m (dimensione della mappa);
•ogni dato è rappresentato dalla coordinata dell’unità su cui
si proietta, cioè quella che ha massima attivazione, cioè
quella per cui i cui pesi sono più simili (vicini) al dato stesso.
Mappe auto-organizzanti (SOM) di Kohonen
In pratica:
•si partiziona lo spazio degli ingressi in tanti sottospazi quanti
sono i neuroni
•ogni sottospazio si di S={Xk} è definito come:
si = {Xj t.che d(Xj,Wi) = mint (Xi,Wt) }
• si ottiene la cosiddetta
Tassellazione di Voronoi
Mappe auto-organizzanti (SOM) di Kohonen
Semplificazioni del modello per implementazione algoritmo di
addestramento:
•si modificano i pesi solo nell’intorno del neurone che ha max
attivazione (neurone vincente, questo tipo di addestramento è
detto anche competitive learning)
•si considerano solo le interazioni laterali eccitatorie all’interno
di un intorno limitato del neurone vincente
NB Modificare i pesi in senso eccitatorio significa renderli più
simili all’ingresso; modificarli in senso inibitorio significa renderli
meno simili.
Mappe auto-organizzanti (SOM) di Kohonen
a=C
(a = learning rate, C costante positiva piccola << 1)
Dato un training set X = { xi | , Xi=(xi1, xi2, ….,, xim), i=1…N }
- Inizializza i pesi con valori compatibili con i dati
- Per ogni esempio xi nel training set:
1. determina l’unità vincente nw
2. modifica i pesi dell’unità vincente e di quelle che si
trovano in un suo intorno nel modo seguente:
3. wj(t+1) = wj (t) + a (xi - wj (t))
4. a(t+1) = a(t) * (1 - g)
(g costante positiva piccola << 1 )
finché la rete non raggiunge una configurazione stabile o a = 0
Mappe auto-organizzanti (SOM) di Kohonen
• Modello semplificato delle interazioni fra neuroni adiacenti la
cui forza ha un andamento tipico a cappello messicano.
Nell’algoritmo si usa un modello semplificato in cui l’attivazione
è uniforme nell’intorno del neurone vincente (a finestra
rettangolare).
• L’ intorno è tipicamente quadrato (per semplicità) ma può
assumere qualunque forma
• E’ possibile prevedere anche un’area che circonda l’intorno
considerato in cui si ha un effetto inibitorio, in cui cioè la regola
diventa
wj(t+1) = wj (t) - a (xi - wj (t))
• Esiste un isomorfismo fra lo spazio di ingresso e lo spazio dei
pesi
Mappe auto-organizzanti (SOM) di Kohonen
Realizzazione di un clustering dei dati, cioè di una
identificazione, nello spazio degli ingressi, di nuvole di dati che
si addensano in zone dello spazio di ingresso, inducendone una
partizione
•ogni partizione è rappresentabile mediante il centroide della
nuvola, che nelle reti di Kohonen corrisponde ai pesi
associati ad una unità della mappa
•il clustering è di tipo non supervisionato, in quanto non
abbiamo alcuna informazione a priori sulle classi di
appartenenza dei dati
•a posteriori è possibile classificare i dati in base alla
partizione dello spazio degli ingressi cui appartengono
Versione supervisionata
(Learning Vector Quantization o LVQ)
• La partizione rappresentabile mediante i pesi associati ad una
unità della mappa rappresenta il prototipo (o una
approssimazione) per una certa classe di dati.
• Vector Quantization = procedura mediante la quale si
definisce un codice di lunghezza limitata che approssima i valori
di dati simili sostituendoli con un codice fisso.
• Il codice è tale da minimizzare l’errore che si commette
sostituendo tale codice ad un insieme di dati vicini (cioè ne è il
centroide). Utilizzabile per la compressione di segnali o
immagini. Es. immagini a colori rappresentate con una palette
di dimensioni limitate.
• Unendo questi concetti è possibile definire un algoritmo di
apprendimento supervisionato con una regola simile alle SOM.
Learning Vector Quantization (LVQ)
a=C
(a = learning rate, C costante positiva piccola << 1)
Dato un training set X = { (xi,li) | , Xi=(xi1, xi2, ….,, xim), i=1…N, liZ}
-Inizializza i pesi con valori compatibili con i dati, assegnando
etichette random ai neuroni corrispondenti (o utilizzando alcuni
degli esempi, che rappresentino tutte le classi )
-Per ogni esempio xi nel training set:
1. determina l’unità vincente nw
2. modifica i pesi dell’unità vincente nel modo
seguente:
3. wj(t+1) = wj (t) + D a (xi - wj (t))
(D =1 se li = lw; D = -1 altrimenti)
4. a(t+1) = a(t) * (1 - g)
(g costante positiva piccola << 1 )
finché la rete non raggiunge una configurazione stabile o
raggiungo un errore sufficientemente basso
Learning Vector Quantization
• Non è più necessario modellare le interazioni laterali fra
neuroni (si effettua un campionamento, non una proiezione
come nel caso delle SOM).
• La rete non è più una mappa, ma un insieme di prototipi
• La classificazione di un dato avviene mediante assegnazione
ad esso dell’etichetta associata all’unità vincente, quindi in
funzione dell’etichetta associata al prototipo che induce la
partizione dello spazio degli ingressi entro cui giace il dato da
classificare.
•Errore valutabile come errore di approssimazione (vector
quantization) o come accuratezza (classificazione)
• Problema del dimensionamento della rete: di quanti prototipi
ho bisogno ?
Learning Vector Quantization
• L’algoritmo LVQ fissa a priori la dimensione della rete
• Se i neuroni sono pochi (partizioni “grandi”), vi è elevata
probabilità che in una partizione giacciano dati appartenenti a
classi diverse
• Se i neuroni sono troppi posso avere overfit (al limite, posso
azzerare l’errore di classificazione sul training set se utilizzo
una rete che ha tanti neuroni quanti esempi nel training set e
pesi uguali agli esempi stessi)
• Si possono usare strategie di dimensionamento dinamico della
rete, in funzione delle prestazioni della rete.
Optimum-Size Learning Vector Quantization
(OSLVQ)
• E’ necessario predisporre un validation set, da utilizzare per
valutare le prestazioni della rete, ai fini di effettuare le modifiche
opportune.
• Modifiche = cancellazioni o inserimento di neuroni
• Se un neurone viene attivato da pattern appartenenti ad una
classe diversa in numero significativo, è necessario inserire un
nuovo neurone corrispondente a tale classe nella partizione
corrispondente.
• Se un neurone non viene mai attivato o se, in sua assenza, i
pattern che giacciono nella sua partizione vengono ugualmente
classificati in modo corretto, si può eliminare il neurone
Optimum-Size Learning Vector Quantization
(OSLVQ)
• Si definiscono le costanti, a, b, g e Niter
•
a = numero max di errori tollerato in una partizione
•
b = numero minimo di pattern che devono attivare un neurone
•
g = numero max di neuroni vicini della stessa classe
• Per ogni Niter iterazioni dell’algoritmo LVQ
•
Se in una partizione Nerr > a si aggiunge un neurone. I pesi sono
uguali alla media dei pattern della classe su cui si commettono più
errori in quella partizione, che cadono in tale partizione.
•
Se il neurone è attivato da Np < b pattern, si elimina il neurone.
•
Se Nn > g neuroni vicini appartengono alla stessa classe, si elimina il
neurone.
finché la rete non si stabilizza o raggiunge prestazioni “sufficienti”