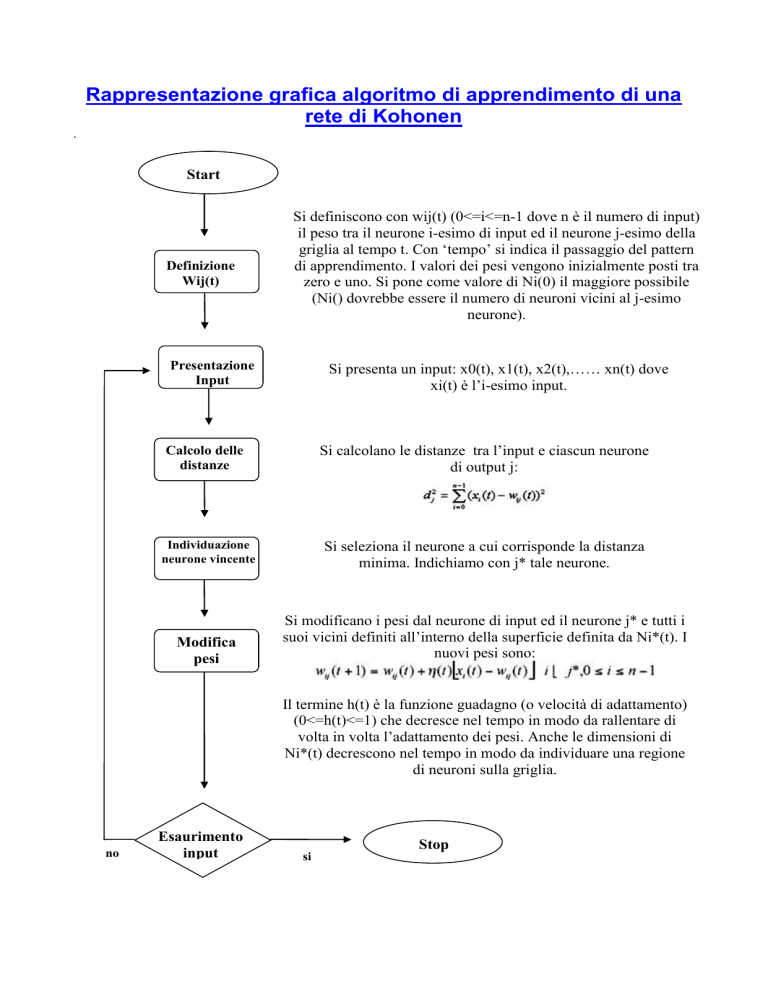
Rappresentazione grafica algoritmo di apprendimento di una
rete di Kohonen
.
Start
Definizione
Wij(t)
Si definiscono con wij(t) (0<=i<=n-1 dove n è il numero di input)
il peso tra il neurone i-esimo di input ed il neurone j-esimo della
griglia al tempo t. Con ‘tempo’ si indica il passaggio del pattern
di apprendimento. I valori dei pesi vengono inizialmente posti tra
zero e uno. Si pone come valore di Ni(0) il maggiore possibile
(Ni() dovrebbe essere il numero di neuroni vicini al j-esimo
neurone).
Presentazione
Input
Si presenta un input: x0(t), x1(t), x2(t),…… xn(t) dove
xi(t) è l’i-esimo input.
Si calcolano le distanze tra l’input e ciascun neurone
di output j:
Calcolo delle
distanze
Individuazione
neurone vincente
Si seleziona il neurone a cui corrisponde la distanza
minima. Indichiamo con j* tale neurone.
Modifica
pesi
Si modificano i pesi dal neurone di input ed il neurone j* e tutti i
suoi vicini definiti all’interno della superficie definita da Ni*(t). I
nuovi pesi sono:
Il termine h(t) è la funzione guadagno (o velocità di adattamento)
(0<=h(t)<=1) che decresce nel tempo in modo da rallentare di
volta in volta l’adattamento dei pesi. Anche le dimensioni di
Ni*(t) decrescono nel tempo in modo da individuare una regione
di neuroni sulla griglia.
no
Esaurimento
input
Stop
si












