Mappe auto-organizzanti (SOM) di Kohonen

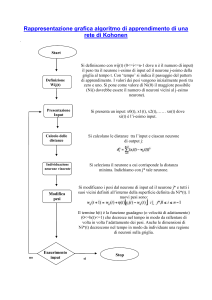
Apprendimento Automatico
Reti Neurali
Apprendimento non supervisionato:
Reti di Kohonen
Stefano Cagnoni
Mappe auto-organizzanti (SOM) di Kohonen
Homunculus
Modello biologico di partenza
Nella corteccia cerebrale esistono mappature
(proiezioni) di stimoli sensoriali su specifiche
reti di neuroni corticali.
I neuroni senso-motori costituiscono una
mappa distorta (l’estensione di ciascuna
regione è proporzionale alla sensibilità della
corrispondente area corporea, non alle
dimensioni) della superficie corporea.
Tuttavia, parti adiacenti della corteccia
corrispondono a parti adiacenti della
superficie corporea.
Mappe auto-organizzanti (SOM) di Kohonen
Interazioni laterali fra neuroni
• eccitazione laterale a breve raggio (50-100 mm)
• azione inibitoria (fino a 200-500 mm)
• azione eccitatoria debole a lungo raggio (fino a qualche cm)
approssimabili come:
Mappe auto-organizzanti (SOM) di Kohonen
Mappe “sensoriali”, costituite da un singolo strato di neuroni
in cui le unità si specializzano a rispondere a stimoli diversi
in modo tale che:
• ingressi di tipo diverso attivino unità diverse
• unità topologicamente vicine vengano attivate da ingressi
simili
Mappe auto-organizzanti (SOM) di Kohonen
•Singolo strato di neuroni ni i=1,w*h (w=largh. h= alt. mappa)
•Ogni ingresso X={xj, j=1,N} è collegato a tutti i neuroni (quindi
ad ogni neurone afferiscono N connessioni)
•Ogni connessione è associata ad un peso wij
•Funzione di attivazione
fi 1/d(Wi,X) d= distanza
•Presenza di interazioni laterali
(proporzionali alla distanza fra neuroni
secondo la funzione a cappello di messicano)
Mappe auto-organizzanti (SOM) di Kohonen
I pesi di ciascun neurone vengono modificati:
• in senso eccitatorio, proporzionalmente al valore della
propria funzione di attivazione e di quelle dei neuroni
appartenenti ad un loro vicinato e in funzione della distanza da
essi;
• in senso inibitorio, proporzionalmente al valore della funzione
di attivazione dei neuroni esterni al vicinato e in funzione della
distanza da essi.
Quindi, se si ripropone lo stesso ingresso alla rete:
• i neuroni che avevano un valore elevato di attivazione e i
vicini mostreranno un’attivazione ancora maggiore
• i neuroni che rispondevano poco risponderanno ancor meno
Mappe auto-organizzanti (SOM) di Kohonen
Se si presentano alla rete dati ben distribuiti nello spazio
degli ingressi, in modo iterativo, ogni neurone si specializza
a rispondere a dati di un certo tipo
Inoltre, neuroni vicini rispondono a stimoli vicini proiettando,
in pratica, lo spazio degli ingressi sullo strato di neuroni.
Risultati:
• riduzione di dimensionalità dei dati da N (dim. dell’ingresso)
a m (dimensione della mappa);
• ogni dato è rappresentato dalla coordinata dell’unità su cui
si proietta, cioè quella in cui il dato genera la massima
attivazione, cioè quella per cui i cui pesi sono più simili
(vicini) al dato stesso.
Mappe auto-organizzanti (SOM) di Kohonen
In pratica:
• una SOM su cui sia stato operato il training partiziona lo
spazio degli ingressi in tanti sottospazi quanti sono i neuroni
• ogni sottospazio si di S={Xk} è definito come:
si = {Xj t.che d(Xj,Wi) = mint (Xi,Wt) }
• si ottiene la cosiddetta
Tassellazione di Voronoi
dello spazio di ingresso
Mappe auto-organizzanti (SOM) di Kohonen
Semplificazioni del modello per implementazione algoritmo di
addestramento:
• si modificano i pesi solo nell’intorno del neurone che ha max
attivazione (neurone vincente, questo tipo di addestramento è
detto anche competitive learning)
• si considerano solo le interazioni laterali eccitatorie all’interno
di un intorno limitato del neurone vincente
NB Modificare i pesi in senso eccitatorio significa renderli più
simili all’ingresso (si incrementa l’attivazione in corrispondenza
dell’ingresso stesso); modificarli in senso inibitorio significa
renderli meno simili (l’attivazione diminuisce).
Mappe auto-organizzanti (SOM) di Kohonen
a=C
(a = learning rate, C costante positiva piccola << 1)
Dato un training set X = { xi | , Xi=(xi1, xi2, ….,, xim), i=1…N }
- Inizializza i pesi con valori compatibili con i dati
- Per ogni esempio xi nel training set:
1. determina l’unità vincente nw
2. modifica i pesi dell’unità vincente e di quelle che si
trovano in un suo intorno nel modo seguente:
3. wj(t+1) = wj (t) + a (xi - wj (t))
4. a(t+1) = a(t) * (1 - g)
(g costante positiva piccola << 1 )
finché la rete non raggiunge una configurazione stabile o a = 0
Mappe auto-organizzanti (SOM) di Kohonen
• Modello semplificato delle interazioni laterali fra neuroni
adiacenti la cui intensità ha un andamento tipico a cappello
messicano. Nell’algoritmo si usa un modello semplificato in cui
l’attivazione è uniforme nell’intorno del neurone vincente (a
finestra rettangolare).
• L’intorno è tipicamente quadrato (per semplicità) ma può
assumere qualunque forma (comune anche esagonale)
• E’ possibile prevedere anche un’area che circonda l’intorno
considerato in cui si ha un effetto inibitorio, in cui cioè la regola
diventa
wj(t+1) = wj (t) - a (xi - wj (t))
• Esiste un isomorfismo fra lo spazio di ingresso e lo spazio dei
pesi
Mappe auto-organizzanti (SOM) di Kohonen
Realizzano il clustering dei dati, cioè l’identificazione, nello
spazio degli ingressi, di nuvole di dati che si addensano in zone
dello spazio di ingresso, inducendone una partizione
• ogni partizione è rappresentabile mediante il centroide
della nuvola, che nelle reti di Kohonen corrisponde ai pesi
associati ad una unità della mappa
• il clustering è di tipo non supervisionato, in quanto non
abbiamo alcuna informazione a priori sulle classi di
appartenenza dei dati
• a posteriori è possibile classificare i dati in base alla
partizione dello spazio degli ingressi cui appartengono
Versione supervisionata
(Learning Vector Quantization o LVQ)
• La partizione di cui è centroide il vettore dei pesi associati ad
una unità della mappa rappresenta il prototipo (o una
approssimazione) per una certa classe di dati.
• Vector Quantization = procedura mediante la quale si
definisce un codice di lunghezza limitata che approssima i valori
di dati simili sostituendoli con un codice fisso.
• Il codice è tale da minimizzare l’errore che si commette
sostituendo ad un insieme di dati vicini lo stesso elemento (il
centroide dei dati) di tale codice. Utilizzabile per la
compressione di segnali o immagini. Es. immagini a colori
rappresentate con una palette di dimensioni limitate.
• Unendo questi concetti è possibile definire un algoritmo di
apprendimento supervisionato con una regola simile alle SOM.
Learning Vector Quantization (LVQ)
a=C
(a = learning rate, C costante positiva piccola << 1)
Dato un training set X = { (xi,li) | , Xi=(xi1, xi2, ….,, xim), i=1…N, liZ}
- Inizializza i pesi con valori compatibili con i dati, assegnando
etichette random ai neuroni corrispondenti (o utilizzando alcuni degli
esempi), purché rappresentino tutte le classi.
- Per ogni esempio xi nel training set:
1. determina l’unità vincente nw
2. modifica i pesi dell’unità vincente nel modo seguente:
3. wj(t+1) = wj (t) + D a (xi - wj (t))
(D =1 se li = lw; D = -1 altrimenti)
4. a(t+1) = a(t) * (1 - g)
(g costante positiva piccola << 1 )
finché la rete non raggiunge una configurazione stabile o finché non
si raggiunge un errore sufficientemente basso
Learning Vector Quantization
• Non è più necessario modellare le interazioni laterali fra
neuroni: si effettua una quantizzazione, non una proiezione
come nel caso delle SOM.
• La rete non è più una mappa, ma un insieme di prototipi
indipendenti l’uno dall’altro
• La classificazione di un dato avviene assegnando al dato
l’etichetta associata al prototipo che rappresenta la partizione
dello spazio degli ingressi entro cui si colloca il dato, cioè il
prototipo più vicino al dato.
• Errore valutabile come errore di approssimazione (vector
quantization) o come accuratezza (classificazione)
• Problema del dimensionamento della rete: di quanti prototipi
ho bisogno ?
Learning Vector Quantization
• L’algoritmo LVQ fissa a priori la dimensione della rete.
• Se i neuroni sono pochi (partizioni “grandi”), vi è elevata
probabilità che in una partizione giacciano dati appartenenti a
classi diverse.
• Se i neuroni sono troppi posso avere overfit.
Al limite, posso azzerare l’errore di classificazione sul training
set se utilizzo una rete che ha tanti neuroni quanti esempi nel
training set e pesi uguali agli esempi stessi.
• Si possono usare strategie di dimensionamento dinamico della
rete, in funzione delle prestazioni della rete.
Optimum-Size Learning Vector Quantization
(OSLVQ)
• E’ necessario predisporre un validation set, da utilizzare per
valutare le prestazioni della rete, ai fini di effettuare le modifiche
opportune.
• Modifiche = cancellazioni o inserimento di neuroni
• Se un neurone viene attivato da pattern appartenenti ad una
classe diversa in numero significativo, è necessario inserire un
nuovo neurone corrispondente a tale classe nella partizione
corrispondente.
• Se un neurone non viene mai attivato o se, in sua assenza, i
pattern che giacciono nella sua partizione vengono ugualmente
classificati in modo corretto, si può eliminare il neurone
Optimum-Size Learning Vector Quantization
(OSLVQ)
• Si definiscono le costanti, a, b, g e Niter
•
a = numero max di errori tollerato in una partizione
•
b = numero minimo di pattern che devono attivare un neurone
•
g = numero max di neuroni vicini della stessa classe
• Per ogni Niter iterazioni dell’algoritmo LVQ
•
Se in una partizione P si ha che Nerr > a, allora si aggiunge un
neurone. I pesi del nuovo neurone sono inizializzati con le
coordinate del centroide (media) dei pattern, appartenenti alla classe
su cui si commettono più errori in P, che cadono in tale partizione.
•
Se il neurone è attivato da Np < b pattern, allora si elimina il neurone.
•
Se Nn > g neuroni vicini appartengono alla stessa classe, si elimina il
neurone.
finché la rete non si stabilizza o raggiunge prestazioni “sufficienti”