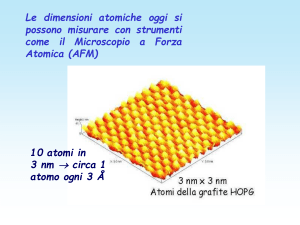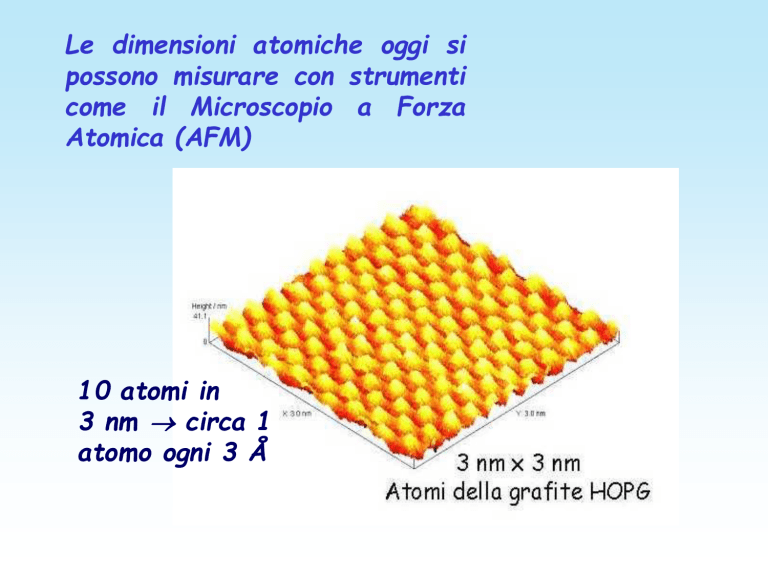
Le dimensioni atomiche oggi si
possono misurare con strumenti
come il Microscopio a Forza
Atomica (AFM)
10 atomi in
3 nm circa 1
atomo ogni 3 Å
Un “miraggio” quantistico
"This STM image shows the
direct
observation
of
standing-wave patterns in
the local density of states
of the Cu(111) surface.
These spatial oscillations
are
quantum-mechanical
interference
patterns
caused by scattering of the
two-dimensional
electron
gas off the Fe atoms and
point defects. "
http://www.almaden.ibm.com/almaden/media/mirage5.html
Struttura della Materia I°- 2004/05
Sito web: http://www.iapht.unito.it/struttura
e-mail:
[email protected]
orario lezioni:
ricevimento:
mercoledì ore 11-13
giovedì e venerdì ore 9-11
venerdì ore 11-13
prossimo esame scritto: 14 marzo 05, ore 9
Esami propedeutici
- meccanica
- onde, fluidi, termodinamica
- elettromagnetismo e ottica
- complementi di elettromagnetismo
- meccanica analitica e statistica
- meccanica quantistica
Programma
0. Richiami di concetti e argomenti propedeutici
1. Fisica atomica e transizioni radiative
2. Fisica molecolare
3. Statistiche quantistiche
4. Introduzione alla fisica dello stato solido
Richiami di concetti
e argomenti propedeutici
• Analisi dimensionale, unità di misura e
costanti naturali
• Atomi idrogenoidi
• Meccanica statistica classica
Unità di misura
- energia : eV (l eV = 1.610-19 joule)
- lunghezza: m, nm, Å (1 ångstrom = 10-10 m)
- tempo: s
- campo magnetico: T, G (tesla, gauss, 1G=10-4 T)
- temperatura : K (gradi kelvin)
come esprimere le grandezze principali:
- la massa m: va moltiplicata per c2 (c è la velocità della
luce) ed espressa in eV
- la quantità di moto p: va moltiplicata per c ed
espressa in eV
- la carica elettrica q: si usa il sistema di unità di
misura di Gauss, in cui kel = 1/4o=1 e l’energia
potenziale elettrica Ep = q Q/r (q e Q= cariche,
r=distanza)
- velocità della luce c = 3108 m s-l
Costanti naturali
- costante di Planck c = 210-7eV m = 2103 eV Å
- costante di struttura fine e2/ ( c) = 1/137
- carica dell’elettrone al quadrato e2 = c/137 = 14,4 eV Å
- raggio dell’atomo di Bohr ao (c)2 / e2mec2 0,53 1010 m
- energia di Rydberg ER = e2/ 2ao =13,6 eV
- numero di Avogadro NA = 61023mole-1
- costante di Boltzmann kB = 8.610-5 eV K-1
- massa dell’elettrone me c2=0.51106 eV
- massa del protone mp c2 = 0.94109 eV
- unità di massa atomica muma c2 = 0.93109 eV
- magnetone di Bohr B =610-5 eV T-1= 0,610-8 eV gauss-1
Atomi idrogenoidi:
descrizione classica
Ze
Potenziale: E p
r
Costanti del moto:
- energia totale
E=Ecin+Ep
L pr
- direzione del momento angolare
L
- momento angolare (modulo)
sono permessi tutti i valori di E e, a parità di E, sono
permessi tutti i valori di L, in modulo e direzione
2
Atomo di idrogeno: descrizione classica del moto di un elettrone
con semiasse maggiore dell’ellisse pari al raggio di Bohr (0,53 Å)
orbita elettrone
0,60
p
orbita con L massimo
0,40
orbita con L inferiore al
massimo
pper
y (angstrom)
0,20
0,00
afelio
perielio
nucleo
paf
-0,20
-0,40
-0,60
-1,20
-1,00
-0,80
-0,60
-0,40
-0,20
0,00
x (angstrom)
0,20
0,40
0,60
0,80
Atomo di idrogeno: energie in funzione di r nel moto classico di un
elettrone con orbita circolare di raggio pari al raggio di Bohr (0,53 Å)
atomo H: momento angolare massimo
50
40
30
energia (eV)
20
10
0
EL
potenziale effettivo Ep+EL
L2
2mr 2
potenziale centrifugo EL
ao
-10
energia totale E
-20
-30
-40
-50
-60
0,00
energia coulombiana Ep
1,00
2,00
Ze2
Ep
r
3,00
distanza dal nucleo (angstrom)
4,00
Atomo di idrogeno: energie in funzione di r nel moto classico di un elettrone
con orbita ellittica di semiasse maggiore pari al raggio di Bohr (0,53 Å)
atomo H: momento angolare qualunque
50
40
30
energia (eV)
20
potenziale effettivo Ep+EL
potenziale centrifugo EL
10
0
-10
-20
energia totale E
perielio
afelio
-30
-40
-50
-60
0,00
energia coulombiana Ep
1,00
2,00
3,00
distanza dal nucleo (angstrom)
4,00
Atomi idrogenoidi:
Ze
Potenziale: E p
descrizione quantistica
r
Numeri quantici:
- n energia totale
En= - ERZ2/n2
- l momento angolare
L2 = l(l+1) 2
- ml componente di L lungo
Lz= ml
l’asse di quantizzazione
sono permessi solo i valori di E, L2, Lz corrispondenti
ai valori interi dei numeri quantici
n1 ; 0 l < n ; -l ml l
2
Energia (eV)
Atomo di idrogeno: livelli energetici ed energia potenziale l=0
0,0
n=3
n=2
-5,0
punti di inversione del moto
-10,0
n=1
-15,0
-20,0
Potenziale e livelli energetici
-25,0
-30,0
0,00
2,00
4,00
6,00
r (angstrom)
8,00
10,00
12,00
Atomo di idrogeno: equazione di Schrödinger
2
2
pr2
L
Ze
(r , , ) E (r , , )
H (r , , )
2m 2mr 2
r
(r , , ) R(r )Yl
ml
u (r ) ml
( , )
Yl ( , )
r
2 ml
2 ml
L Yl (, ) l (l 1) Yl (, )
interpretazione fisica della “funzione d’onda”
2 2
( r, , ) r dr dΩ
probabilità
di
z
trovare
l’elettrone nell’elemento di
r
y
volume r 2dr dΩ intorno al
punto (x,y,z)
x
oggi (r, , ) 2 si misura direttamente con il
Microscopio a Forza Atomica (AFM)
termini di energia “di posizione”
termine cinetico
2 d 2u (r ) l (l 1) 2 Ze 2
E u (r )
2m dr 2
2mr 2
r
curvatura della funzione d’onda
2
d u (r )
dr
2
funzione d’onda
Eeff E u (r )
2
2m
Eeff = EL + Ep
coefficiente di proporzionalità
Funzioni d'onda
l =0
r (angstrom)
14,0
12,0
0
2
4
10,0
8
10
12
punti di flesso
n=3
8,0
6,0
6
n=1
Atomo di idrogeno: l=0
Eeff =Ep
4,0
2,0
0,0
-2,0
n=2
-4,0
-6,0
Energia (eV)
-8,0
0,0
-10,0
n=2
-5,0
-10,0
- i punti di inversione del
moto classico sono punti di
flesso della funzione
d’onda perché E-Eeff=0
n=3 - il numero di “nodi” della
funzione d’onda aumenta
con n
n=1
-15,0
punti di inversione
-20,0
Potenziale e livelli energetici
-25,0
-30,0
0,00
2,00
4,00
6,00
r (angstrom)
8,00
10,00
12,00
Energia (eV)
Atomo di idrogeno: livelli energetici ed energia potenziale l=1 e 2
30.0
20.0
punti di inversione per n=2
n=2, l=0
n=2, l=1
n=2, l=2
EL per l=2
EL per l=1
10.0
Eeff per l=2
0.0
n=3
n=2
Eeff per l=1
-10.0
n=1
-20.0
-30.0
0.00
2.00
4.00
6.00
r (angstrom)
8.00
10.00
12.00
Funzioni d'onda
n =2; l = 0,1
r (angstrom)
10.0
0
5.0
2
4
6
8
10
12
l=1
punti di flesso
Atomo di idrogeno: n=1
Eeff =EL+ Ep
0.0
Energia (eV)
-5.0
l=0
10.0
-10.0
5.0
0.0
n=2
-5.0
-10.0
- i punti di inversione del
moto classico sono punti di
flesso della funzione
d’onda perché E-Eeff=0
n=3 - il numero di “nodi” della
funzione d’onda
diminuisce con l
n=1
punti di inversione
-15.0
-20.0
-25.0
-30.0
-35.0
0.00
2.00
4.00
6.00
r (angstrom)
8.00
10.00
12.00
Le dimensioni atomiche
….. oggi si possono misurare con
strumenti come il Microscopio a
Forza Atomica (AFM)
Il “raggio di Bohr”
ao=0,53 ·10-10m
ao
h2
4 e me
2 2
c
mec
2
dipende solo dalle costanti
naturali (h, c, e, me) che
compaiono nell’equazione di
Schrödinger
10 atomi in
3 nm circa 1
atomo ogni 3 Å
conviene introdurre la
“distanza ridotta ”,
tale che:
nao
r
2Z
ao determina la rapidità della
caduta esponenziale della funzione
d’onda dopo l’ultimo flesso
il flesso
• si “allontana” al crescere di n
•si “avvicina” al crescere di Z
l 0
u10 ( r ) 2 C r e / 2
n2
l 0
u20 ( r )
1
n2
l 1
u21 ( r )
n 1
2 2
1
C r (2 ) e / 2
2 6
C r e / 2
“orbitale” 1s
1s
6,00
funzione d'onda
5,00
4,00
3,00
2,00
1,00
0,00
-4
-3
-2
-1
0
1
z (angstrom)
2
3
4
Z
“orbitale” atomico 2pz
2pz
Z
0,25
andamento in
0,20
funzione di x a z>00,15
funzione d'onda
0,10
0,05
0,00
-0,05
-0,10
X
-0,15
andamento in
-0,20
funzione di x-0,25a z<0
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
x (angstrom)
2pz
0,15
funzione d'onda
0,10
0,05
andamento in
funzione di z a x,y=0
0,00
-0,05
-0,10
-0,15
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
z (angstrom)
3
4
5
6
7
8
3
4
5
6
7
8
Livelli energetici: diagramma di Grotrian
E (eV)
4 -0.85
3 -1.5
2 -3.4
1 -13.6
rappresentazione n,l,ml ,ms>
(2)
(6)
(10)
(2)
(6)
(10)
(2)
(6)
(2)
0
n
0
s
-1
0
1
p
+1
-2 -1 0 +1 +2
2
d
ml
l
Livelli energetici
E (eV)
4 -0.85
3 -1.5
2 -3.4
1 -13.6
n
rappresentazione n, l, j ,mj>
(2)
(2)
(4)
(2)
(2)
(4)
(4)
(6)
(2)
mj
-1/2 +1/2
-1/2 +1/2
1/2
1/2
0
s
-3/2 -1/2 +1/2 +3/2
3/2
1
p
-3/2 -1/2 +1/2 +3/2
3/2
2
d
-5/2 -3/2 -1/2 +1/2 +3/2 +5/2
5/2
j
l
trasformazione da una base all’altra
n, l, j ,mj> =
2,1, 3/2 ,+1/2>
ml=1, ms= -1/2
mj = 1/2 si può ottenere con
ml=0, ms= +1/2
2,1, 3/2 ,+1/2> = a 2,1, 1 ,-1/2> + b 2,1, 0 ,+1/2>
coefficienti di Clebsch Gordon
a = 2/3
b = 1/3
tabella dei coefficienti di Clebsch - Gordan
ml m s
+1 +1/2
+1 -1/2
0 +1/2
0 -1/2
-1 +1/2
-1
-1/2
3/2 j
+3/2 mj
1
1
1
2
3/2 1/ 2 j
+1/ 2 +1/2 mj
1/3 2/3
2/3 -1/3
3/2 1/ 2 j
-1/ 2 -1/2 mj
2/3 1/3
1/3 -2/3
3/2
-3/2
1
j
mj