Presentazione di PowerPoint

Atomi idrogenoidi:
descrizione classica
Ze
Potenziale: E p  
r
Costanti del moto:
- energia totale
E=Ecin+Ep
L  pr

- direzione del momento angolare
L
- momento angolare (modulo)
sono permessi tutti i valori di E e, a parità di E, sono
permessi tutti i valori di L, in modulo e direzione
2
Orbita
classica
Atomo di idrogeno: moto di un elettrone con
semiasse maggiore dell’ellisse pari al
raggio di Bohr (0,53 Å)
orbita elettrone
0,60
p
orbita con L massimo
0,40
orbita con L inferiore al
massimo
pper
y (angstrom)
0,20
0,00
afelio
perielio
nucleo
paf
-0,20
-0,40
-0,60
-1,20
-1,00
-0,80
-0,60
-0,40
-0,20
0,00
x (angstrom)
0,20
0,40
0,60
0,80
Orbita
classica
Atomo di idrogeno: energie in funzione di r nel moto
classico di un elettrone con orbita circolare
di raggio pari al raggio di Bohr (0,53 Å)
atomo H: momento angolare massimo
50
40
30
energia (eV)
20
10
0
EL 
potenziale effettivo Ep+EL
L2
2mr 2
potenziale centrifugo EL
ao
-10
energia totale E
-20
-30
-40
-50
-60
0,00
energia coulombiana Ep
1,00
2,00
Ze2
Ep  
r
3,00
distanza dal nucleo (angstrom)
4,00
Orbita
classica
Atomo di idrogeno: energie in funzione di r nel moto
classico di un elettrone con orbita ellittica di semiasse
maggiore pari al raggio di Bohr (0,53 Å)
atomo H: momento angolare qualunque
50
40
30
energia (eV)
20
potenziale effettivo Ep+EL
potenziale centrifugo EL
10
0
-10
-20
energia totale E
perielio
afelio
-30
-40
-50
-60
0,00
energia coulombiana Ep
1,00
2,00
3,00
distanza dal nucleo (angstrom)
4,00
Atomi idrogenoidi:
descrizione quantistica
Ze
Potenziale: E p  
r
Numeri quantici:
- n  energia totale
En= - ERZ2/n2
- l  momento angolare
L2 = l(l+1)  2
- ml  componente di L lungo
Lz= ml 
l’asse di quantizzazione
sono permessi solo i valori di E, L2, Lz corrispondenti
ai valori interi dei numeri quantici
n1 ; 0  l < n ; -l  ml  l
2
Energia (eV)
Atomo di idrogeno: livelli energetici ed energia potenziale l=0
0,0
n=3
n=2
-5,0
punti di inversione del moto
-10,0
n=1
-15,0
-20,0
Potenziale e livelli energetici
-25,0
-30,0
0,00
2,00
4,00
6,00
r (angstrom)
8,00
10,00
12,00
Atomo di idrogeno: equazione di Schrödinger
2
2
 pr2
L
Ze
 (r , ,  )  E (r , ,  )
H (r , ,  )  


 2m 2mr 2

r


 (r , ,  )  R(r )Yl
ml
u (r ) ml
( ,  ) 
Yl ( ,  )
r
2 ml
2 ml
L Yl (,  )  l (l  1) Yl (,  )
interpretazione fisica della “funzione d’onda
z
2 2
 ( r, , ) r dr dΩ

probabilità di trovare l’elettrone
2
nell’elemento di volume r dr dΩ
intorno al punto (x,y,z)
r
y

|u(r)|2 dr
x
probabilità di trovare l’elettrone a
una distanza fra r e r+dr
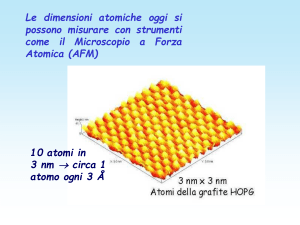
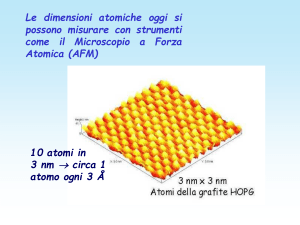
Oggi il valore medio di  (r, , ) 2si può misurare direttamente,
ad es. con un Microscopio a Forza Atomica (AFM)
Funzione d’onda radiale
termini di energia “di posizione”
termine cinetico
  2  d 2u (r )  l (l  1) 2 Ze 2





 E u (r )
 2m  dr 2
 2mr 2

r




curvatura della funzione d’onda
2
d u (r )
dr
2


Eeff  E  u (r )
2
funzione d’onda
2m

Eeff = EL + Ep
coefficiente di proporzionalità
Le dimensioni atomiche
conviene introdurre
la “distanza ridotta
”, tale che:
nao
r

2Z
ao è il “raggio di Bohr”
ao 
h2
4 2e2me

c
10

0
,
53

10
m
2
 mec
dipende solo dalle costanti naturali (h, c, e, me) che compaiono
nell’equazione di Schrödinger
u10 (r )  Cre
 / 2
nao/Z determina la rapidità della caduta
esponenziale della funzione d’onda dopo il flesso
Funzione d'onda
n=1
14,0
12,0
0
1
2
3
4
r (angstrom)
5
6
punto di flesso
10,0
Atomo di idrogeno:
n=1
Eeff =Ep
8,0
6,0
4,0
2,0
0,0
-2,0
-4,0
-6,0
Energia (eV)
-8,0
0,0
-10,0
-5,0
-10,0
n=1
-15,0
punto di inversione
-20,0
Potenziale e livelli energetici
-25,0
-30,0
0,00
1,00
2,00
3,00
r (angstrom)
4,00
5,00
6,00
- i punti di inversione del
moto classico sono punti di
flesso della funzione
d’onda perché E-Eeff=0
- dopo il flesso, la curvatura
della funzione d’onda
cambia segno e la funzione
tende a zero
asintoticamente
Funzioni d'onda
l =0
r (angstrom)
14,0
12,0
0
2
4
10,0
8
10
12
punti di flesso
n=3
8,0
6,0
6
n=1
Atomo di idrogeno:
l=0, n=1, 2, 3
Eeff =Ep
4,0
2,0
0,0
-2,0
n=2
-4,0
-6,0
Energia (eV)
-8,0
0,0
-10,0
n=3
n=2
-5,0
- il numero di “nodi” della
funzione d’onda aumenta
con n
-10,0
n=1
-15,0
punti di inversione
-20,0
- dopo l’ultimo flesso, la
funzione d’onda tende a
zero asintoticamente
Potenziale e livelli energetici
-25,0
-30,0
0,00
- i punti di inversione del
moto classico sono punti di
flesso della funzione
d’onda perché E-Eeff=0
2,00
4,00
6,00
r (angstrom)
8,00
10,00
12,00
Energia (eV)
Atomo di idrogeno: livelli energetici ed energia potenziale
n=2, l=0 e 1
30,0
n=2, l=0
n=2, l=1
20,0
EL per l=1
10,0
Eeff per l=1
0,0
-10,0
flesso di l=0
flessi di l=1
n=1
Potenziale e livelli energetici
-20,0
-30,0
0,00
n=3
n=2
2,00
4,00
6,00
r (angstrom)
8,00
10,00
12,00
Funzioni d'onda
n =2; l = 0,1
r (angstrom)
10.0
0
5.0
2
4
6
8
10
12
l=1
punti di flesso
0.0
Eeff =EL+ Ep
Energia (eV)
-5.0
l=0
- i punti di inversione del
moto classico sono punti di
n=3
flesso della funzione
n=2
d’onda perché E-Eeff=0
- il numero di “nodi” della
n=1
parte radiale della funzione
punti di inversione
d’onda diminuisce con l, a
parità di n
10.0
-10.0
5.0
0.0
-5.0
-10.0
-15.0
-20.0
-25.0
-30.0
-35.0
0.00
Funzione d’onda
radiale n=2, l=0, 1
2.00
4.00
6.00
r (angstrom)
8.00
10.00
12.00
r =  nao/Z, quindi nao/Z
determina la rapidità della caduta
esponenziale della funzione
d’onda dopo l’ultimo flesso
l’andamento per r 0 va
come rl+1
(quello di R(r) va come rl)
Espressione di
u(r) per n=1, 2
il flesso
• si “allontana” al crescere di n
•si “avvicina” al crescere di Z
l 0
u10 ( r )  2 C r e  / 2
n2
l 0
u20 ( r ) 
1
n2
l 1
u21 ( r ) 
n 1
2 2
1
C r (2   ) e  / 2
2 6
C r  e  / 2
integrale del quadrato delle funzioni d'onda
n =1 l = 0; n =2 l = 0,1
r (angstrom)
1,2
0
1,0
n=1
l=0
2
4
6
8
10
12
Andamento vicino
all’origine della
funzione d’onda radiale
0,8
n=2
l=1
0,6
0,4
0,20
integrale del quadrato delle funzioni d'onda
l = 0; n =2 l = 0,1
0
0,5
1
1,5
n= 1
r (angstrom )
2
0,15
n=2, l=0
0,2
0,10
0,0
0,05
Funzioni d'onda
n=1
l=0
10,0
n= 1 l =0; n =2; l = 0,1
0,00
r (angstrom)
n=2
l=1
5,0
- al crescere di n, la
funzione d’onda si sposta
verso l’esterno
0,0
-5,0
n=2, l=0
-10,0
0
2
4
6
8
10
12
- l’andamento per r 0
va come rl
integrale del quadrato delle funzioni d'onda
n =1, 2, 3 e tutti i valori di l
1,2
1,0
n=1 l=0
n=3, l=2
0,8
n=2
l=1
0,6
0,4
integrale del quadrato delle funzioni d'onda
n =1, 2, 3 e tutti i valori di l
n=2
l=0
0,15
n=3, l=1
0,10
0,2
n=3, l=0
0,0
0
2
4
6
Funzioni d'onda
8
2
n=3
l=2
4
6
n=3
l=1
4,0
2,0
0,0
-2,0
-4,0
-6,0
10
0,05 12
r (angstrom)
0
6,0
r (angstrom)
n =3; l = 0,1,2
10,0
8,0
Andamento vicino
all’origine della funzione
d’onda radiale n=1, 2, 3
n=3, l=0
8
10
0,00
12
0
r (angstrom)
1
2
3
4
- al crescere di n, la
funzione d’onda si sposta
verso l’esterno
- l’andamento per r 0
va come rl
u10 ( r ) 0
0
100 ( r, ,  )  R10 ( r )Y0 ( ,  ) 
Y0 ( ,  )  Ce r / ao
r
1s
6,00
Dipendenza angolare:
“orbitale” 1s
funzione d'onda
5,00
4,00
3,00
2,00
1,00
0,00
-4
-3
-2
-1
0
1
z (angstrom)
2
3
4
Z
u21 ( r ) 0
0
 210 ( r, , )  R21 ( r )Y1 ( , ) 
Y1 ( , )  C (2  r / ao )e r / 2ao cos
r
Z
andamento in
funzione di x a z>00,25
2pz
0,20
0,15
funzione d'onda
0,10
X
0,05
0,00
-0,05
-0,10
andamento in
-0,15
funzione di x-0,20a z<0
2pz
-0,25
0,15
-8
-7 -6
-5
-4 -3
-2 -1 0 1 2
x (angstrom)
3
4
5
6
funzione d'onda
0,10
0,05
andamento in funzione di z
per x = 0, y = 0
0,00
-0,05
-0,10
-0,15
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
z (angstrom)
3
4
5
6
7
8
“orbitale” atomico 2p0
7
8
 211 ( r, , )  R21 ( r )Y11( , )  C (2  r / ao )e r / 2ao sen ei
 C (2  r / ao )e r / 2ao sen  (cos   i sen  )
parte
immaginaria
parte reale
_
+
_
+
“orbitale” atomico 2p+
Livelli energetici: diagramma di Grotrian
E (eV)
4 -0.85
3 -1.5
2 -3.4
1 -13.6
rappresentazione n,l,ml ,ms>
(2)
(6)
(10)
(2)
(6)
(10)
(2)
(6)
(2)
0
n
0
s
-1
0
1
p
+1
-2 -1 0 +1 +2
2
d
ml
l