Lezione 2
Evoluzione dei modelli atomici
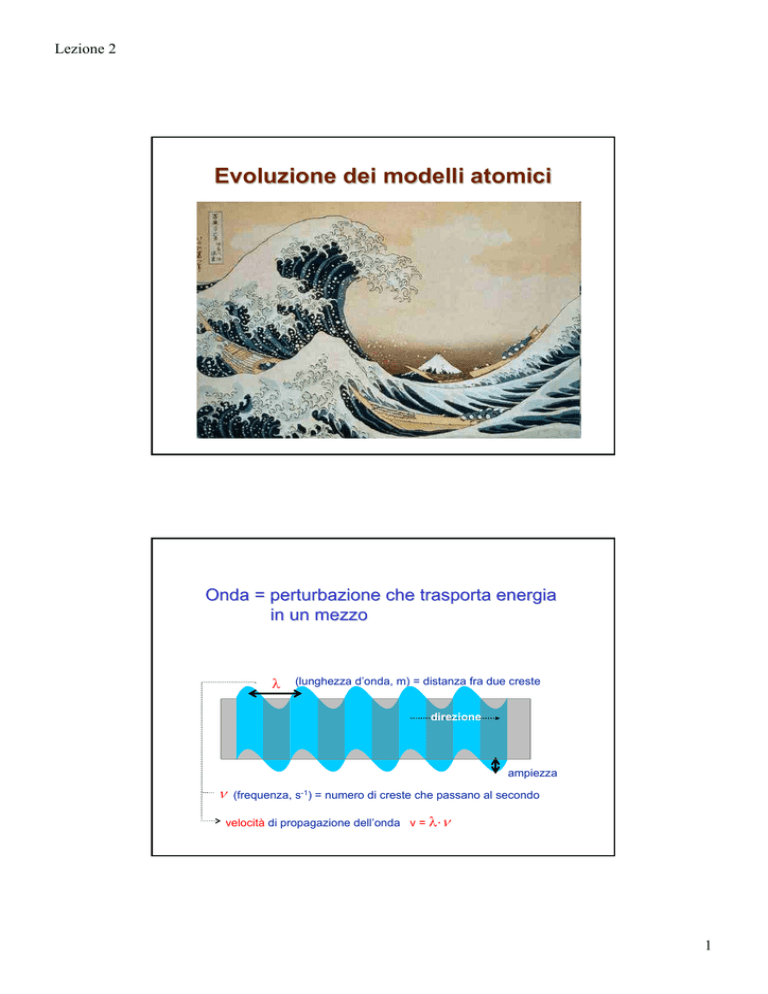
Onda = perturbazione che trasporta energia
in un mezzo
λ
(lunghezza d’onda, m) = distanza fra due creste
direzione
ampiezza
ν
(frequenza, s-1) = numero di creste che passano al secondo
velocità di propagazione dell’onda v = λ⋅ν
1
Lezione 2
Luce: una radiazione elettromagnetica
Radiazione Elettromagnetica
La luce ha una componente elettrica
La luce ha una componente magnetica.
Per la radiazione elettromagnetica v = c ≈ 3 108 m/s (costante!)
perciò vale:
c = ν⋅ λ
λ = 700 nm
λ = 400 nm
Lo spettro elettromagnetico
FIGURA 9-3 Lo spettro elettromagnetico
Piccin Nuova Libraria S.p.A.
2
Lezione 2
• Gli elettroni devono muoversi attorno al nucleo, altrimenti l’atomo collasserebbe.
3
Lezione 2
Modello planetario dell’atomo
4
Lezione 2
Modello planetario dell’atomo: incongruenze
• Una particella carica che descrive una traiettoria circolare accelera e
quindi dovrebbe emettere energia, precipitando sul nucleo.
Inoltre:
• In base a un modello planetario, posso spostare a piacimento l’orbita di
un satellite, fornendo una certa quantità di energia
…ma per gli elettroni ciò non è possibile!
Gli atomi perturbati emettono luce colorata
FIGURA 9-8 Sorgenti di emissioni di luce
Piccin Nuova Libraria S.p.A.
5
Lezione 2
Gli spettri di emissione atomica sono “a righe”
FIGURA 9-9 Spettro atomico, o a righe, dell’elio
Piccin Nuova Libraria S.p.A.
Spettro di emissione dell’atomo di idrogeno
Equazione di Rydberg
⎡1
1⎤
= RH ⎢ 2 − 2 ⎥
λ
⎣ n1 n 2 ⎦
1
RH = 1.097 107 m-1
n1 = 2 “serie di Balmer”
6
Lezione 2
Teoria dei quanti: Max Planck (1900)
EE==hh⋅ ⋅νν
-34
hh==6.62607×10
6.62607×10-34JJss
Modello atomico di Bohr (1913)
L
v
r
L=mr×v
• L’elettrone si muove in orbite circolari attorno ad un nucleo.
• L’elettrone può muoversi solo in orbite definite.
• L’elettrone in queste orbite non emette energia.
• I valori del momento angolare associati alle orbite permesse sono:
L = n·h/2π con n = 1, 2, … (numero quantico)
• L’elettrone può passare da un’orbita a un’altra assorbendo o emettendo
energia quantizzata.
7
Lezione 2
Orbite di Bohr per l’atomo di idrogeno
rn = n 2 a0
En =
− RH
n2
Orbite di Bohr per l’atomo di idrogeno
FIGURA 9-13 Modello di Bohr dell’atomo di idrogeno
“stato fondamentale”
rn = n 2 a0
r1 = a 0
a0 è il “raggio di Bohr”
a0 = 52.91772108 pm
En =
− RH
n2
E1 = – RH
= – 2.179×10-18 J
= – 1 Ry
8
Lezione 2
Livelli energetici e transizioni elettroniche per H
“stati eccitati”
E3
En =
− RH
n2
E2
ΔE = Ef − Ei = hν
lim E = 0
n→∞
“stato fondamentale” E1 = – RH
E1
• Per atomi “idrogenoidi”:
En =
− Z2R H
n2
OK
OK ma
ma …non
…nonfunziona
funzionaper
peratomi
atomi
con
conpiù
piùelettroni!
elettroni!
Effetto fotoelettrico: la luce può avere un
comportamento corpuscolare
FIGURA 9-12 L’effetto fotoelettrico
Hertz, 1886
Einstein, 1905
9
Lezione 2
La materia: proprietà ondulatorie
Effetto fotoelettrico (Einstein): la luce si può comportare
come una particella (“fotoni”).
Louis DeBroglie (1923): postula che le particelle si possono
comportare come un’onda con:
λ=
E = mc 2
h
h
=
p mv
hν = mc 2
hν
= mc = p
c
h
p=
λ
Diffrazione della luce
lastra fotografica
interferenza
costruttiva
distruttiva
10
Lezione 2
La diffrazione:
una prova del
Rifrazione di raggi X
comportamento ondulatorio dell’elettrone
Davisson & Germer; G.P. Thomson (1927)
utilizzando come reticolo un foglio di metallo:
Raggi X
Fascio di elettroni
Principio di indeterminazione
(Heisenberg, 1927)
Δx Δp ≥
h=
h
2
h
= 1.054 × 10 −34 Js
2π
11
Lezione 2
hν
a0
E1 = –2.179 ×10-18 J
2re ≈ 10-14 m
ν= c/λ ≈ 3×1022 s-1
E = hν ≈ 2×10-11 J !
1927: Schroedinger
FIGURA 9-17 Onde stazionarie in una corda
• L’elettrone all’interno dell’atomo deve
essere rappresentato da onde stazionarie...
che sono quantizzate per loro natura!
• Queste onde sono descritte da funzioni
ψ(x,y,z) chiamate “funzioni d’onda”
• Le ψ si trovano risolvendo un’equazione
differenziale ψ= E ψ
• si postula che ψ2 sia in relazione
con la probabilità di trovare l’elettrone
• Nel caso di una particella confinata
in un potenziale a forma di scatola
12
Lezione 2
L’equazione di Schroedinger
ψ= Eψ
{E,ψ}
Condizioni:
Ψ
è continua,
2
∫ dV Ψ = 1
autovalori, autofunzioni
13












