Parallelismo e perpendicolarità nel piano
Rette perpendicolari
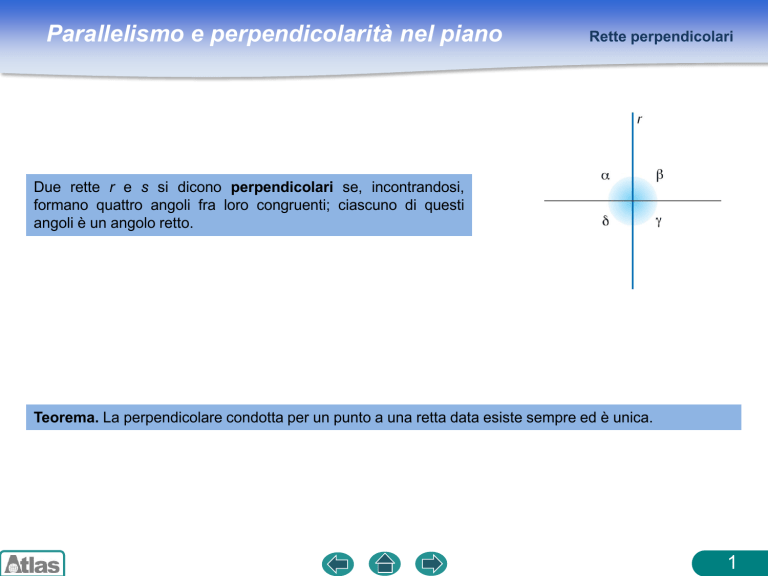
Due rette r e s si dicono perpendicolari se, incontrandosi,
formano quattro angoli fra loro congruenti; ciascuno di questi
angoli è un angolo retto.
Teorema. La perpendicolare condotta per un punto a una retta data esiste sempre ed è unica.
1
Parallelismo e perpendicolarità nel piano
Rette perpendicolari
Il concetto di perpendicolarità permette di introdurre le seguenti definizioni:
Distanza di un punto P da una retta r : segmento di perpendicolare
condotto da P su r.
Il segmento PH è il segmento di minima lunghezza che congiunge P con r.
H: piede, ossia proiezione
ortogonale di P su r.
Proiezione ortogonale di un segmento PQ su una retta r : il
segmento P’Q’ dove P’ e Q’ sono le proiezioni ortogonali di P e Q su r.
2
Parallelismo e perpendicolarità nel piano
Perpendicolarità
a
Asse di un segmento AB: retta a ad esso perpendicolare
passante per il suo punto medio.
Proprietà dell’asse: ogni punto dell’asse è equidistante dagli
estremi del segmento stesso.
K
3
Parallelismo e perpendicolarità nel piano
Perpendicolarità
Dato un triangolo, di dice altezza relativa ad un lato il segmento di perpendicolare condotto dal vertice
opposto su quel lato.
Triangolo acutangolo
Triangolo ottusangolo
Triangolo rettangolo
Teorema. In ogni triangolo isoscele la bisettrice dell’angolo al
vertice è anche mediana e altezza.
4
Parallelismo e perpendicolarità nel piano
Rette parallele
Due rette si dicono parallele se non si intersecano oppure se sono coincidenti.
L’esistenza di tali rette è garantita dal teorema:
Teorema. Se due rette distinte s e t sono perpendicolari ad una
stessa retta r, allora non hanno alcun punto in comune.
La relazione di parallelismo è:
Riflessiva: ogni retta è parallela a se stessa perché questo
equivale a considerare due rette coincidenti
r
s
Simmetrica: se r ⁄⁄ s anche s ⁄⁄ r
Transitiva: se r ⁄⁄ s e s ⁄⁄ t anche r ⁄⁄ t.
t
5
Parallelismo e perpendicolarità nel piano
Rette parallele
Direzione è la caratteristica comune a tutte le rette che sono tra loro parallele.
L’insieme di tutte le rette che hanno la stessa direzione si dice
fascio di rette parallele o fascio di rette improprio.
L’unicità della retta parallela è garantita dal seguente assioma
(Quinto postulato di Euclide)
P
A13. Dati una retta r ed un punto P che non le appartiene, la
parallela ad r per P è unica.
r
6
Parallelismo e perpendicolarità nel piano
Rette parallele
Angoli formati da due rette tagliate da una trasversale t :
Alterni interni: γ e α’ o δ e β’
Alterni esterni: α e γ’ o β e δ’
Corrispondenti: α e α’ o β e β’ o γ e γ’ o δ e δ’
Coniugati interni: γ e β’ o δ e α’
Coniugati esterni: β e γ’ o α e δ’
Se le rette a e b sono parallele:
gli angoli alterni sono congruenti
gli angoli corrispondenti sono congruenti
gli angoli coniugati sono supplementari
7
Parallelismo e perpendicolarità nel piano
Rette parallele
Per riconoscere se due rette sono parallele si applica il seguente criterio.
Criterio generale di parallelismo. Due rette sono parallele se, tagliate da una trasversale, formano:
angoli alterni congruenti, oppure
angoli corrispondenti congruenti, oppure
angoli coniugati supplementari.
Angoli alterni congruenti
Angoli corrispondenti congruenti
Angoli coniugati supplementari
8
Parallelismo e perpendicolarità nel piano
Triangoli
Secondo teorema dell’angolo esterno
Teorema. In ogni triangolo ciascun angolo esterno è congruente
alla somma degli angoli interni ad esso non adiacenti.
ACD
≅ ABC + BAC
Teorema. La somma degli angoli interni di un triangolo è congruente ad un angolo piatto.
ABC + BAC + ACB = π
9
Parallelismo e perpendicolarità nel piano
Poligoni
Da questa proprietà discende che:
Gli angoli acuti di un triangolo rettangolo sono complementari.
La somma degli angoli interni di un poligono convesso di n lati
è congruente a n – 2 angoli piatti.
10
Parallelismo e perpendicolarità nel piano
Poligoni
La somma degli angoli esterni di un poligono convesso è
sempre congruente a due angoli piatti.
Se due triangoli hanno due angoli ordinatamente congruenti,
hanno congruente anche il terzo angolo.
P
r
Si chiama distanza fra due rette parallele la distanza PQ di un punto
qualunque di una di esse dall’altra.
s
Q
11
Parallelismo e perpendicolarità nel piano
CRITERI
Poligoni
DI CONGRUENZA PER I TRIANGOLI RETTANGOLI
Teorema. Due triangoli rettangoli sono congruenti se hanno ordinatamente congruenti:
i due cateti, oppure
un cateto e un angolo acuto, oppure
l’ipotenusa e un angolo acuto, oppure
l’ipotenusa e un cateto.
Ipotenusa e angolo acuto congruenti
Cateti congruenti
Cateto e angolo acuto congruenti
Ipotenusa e cateto congruenti
12












