Presentazione di PowerPoint

2. Variazione del reddito
QB
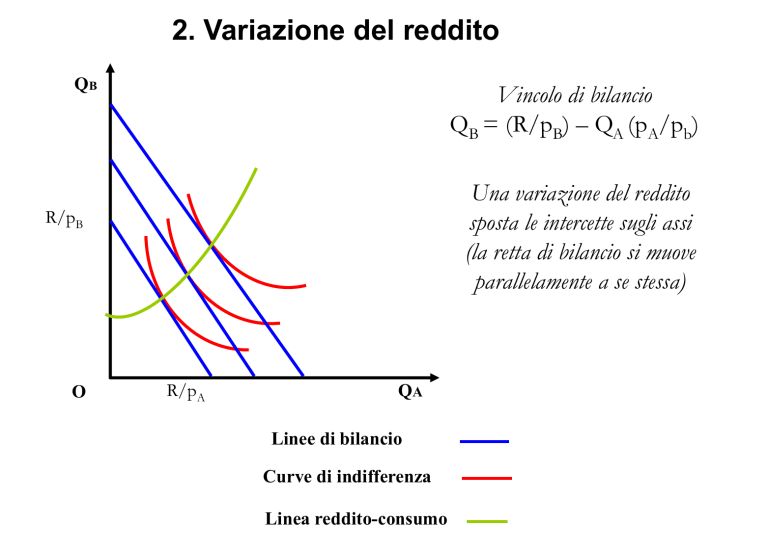
Vincolo di bilancio
QB = (R/pB) – QA (pA/pb)
Una variazione del reddito
sposta le intercette sugli assi
(la retta di bilancio si muove
parallelamente a se stessa)
R/pB
O
R/pA
QA
Linee di bilancio
Curve di indifferenza
Linea reddito-consumo
Attraverso variazioni successive di reddito è possibile identificare la linea di reddito - consumo
che ci introduce alla funzione di domanda di un bene rispetto al reddito
QB
R1
R
R2 > R1
R3
R2
R1
R3 > R2
O
Q1
Q2
Q3
Curve di indifferenza
Linea reddito -consumo
Linee di bilancio
QA
Q1
Q2
Q3
QA
Curve di domanda (Curva di Engel)
rispetto al reddito (caso di bene normale)
ESISTONO ANCHE BENI “INFERIORI”
3. Variazione dei prezzi dei beni
QB
Vincolo di bilancio
QB = (R/pB) – QA (pA/pb)
O
R/pA
R/p*A
QA
Se varia uno dei due prezzi oppure variano entrambi in proporzioni diverse, cambia
l’inclinazione della retta di bilancio
Ad esempio se diminuisce il prezzo di A, il vincolo di bilancio diventa più piatto
La variazione del punto di equilibrio (passaggio da X1 a X2) è denominata effetto
prezzo
Attraverso variazioni successive di prezzo è possibile identificare la linea di prezzo- consumo
che ci introduce alla funzione di domanda di un bene rispetto al prezzo
QB
PA1
pA
PA2 < PA1
PA1
PA2
PA3 < PA2
O
Q1
Q2 Q3
QA
PA3
Q1
Q2 Q3
Curve di indifferenza
Curve di domanda
Linea prezzo-consumo
Linee di bilancio
QA
Scomposizione dell’effetto prezzo in:
EFFETTO REDDITO
Variazione della quantità
richiesta di un bene derivante
dalla variazione del reddito reale
EFFETTO SOSTITUZIONE
Variazione della quantità richiesta
di un bene che deriva dalla
variazione del saggio di scambio
(di trasformazione) (prezzi relativi)
tra i due beni
La scomposizione nei due effetti può essere visualizzata
attraverso tre metodi:
1. Metodo delle variazioni equivalenti di reddito
2. Metodo delle variazioni compensative di reddito
3. Metodo delle variazioni compensative di costo (metodo di Slutsky)
1. Metodo delle variazioni equivalenti di reddito
L’effetto sostituzione si
visualizza sulla curva di
indifferenza di arrivo
QB
X3
X2
X1
O
X1  X2
effetto prezzo
QA
X1  X3 effetto reddito
X3  X2 effetto sostituzione
Aumento ipotetico del reddito che provoca un
aumento equivalente, a parità di prezzi, in
termini di utilità
Variazione della domanda al variare dei prezzi
mantenendo costante l’utilità finale (siamo sulla
curva di indifferenza finale)
2.
Metodo delle variazioni compensative di reddito
QB
L’effetto sostituzione si
visualizza sulla curva di
indifferenza di partenza
X2
X1
X3
QA
O
X2  X3 effetto reddito
X1  X2
effetto prezzo
X1  X3 effetto sostituzione
di Hicks
Diminuzione ipotetica del reddito che
compensa l’aumento di utilità che consegue alla
diminuzione del prezzo
Variazione della domanda al variare dei prezzi
mantenendo costante l’utilità (siamo sulla curva
di indifferenza iniziale)
Curva di domanda compensata (hicksiana)
3. Metodo delle variazioni compensative di costo
(o metodo di Slutsky)
QB
L’effetto sostituzione si
visualizza sulla curva di
indifferenza intermedia
X2
X1
X3
O
QA
X2  X3 effetto reddito
Diminuzione ipotetica del reddito che consente,
ai nuovi prezzi, di acquistare il paniere iniziale
X1  X2
effetto prezzo
X1  X3 effetto sostituzione
di Slutsky
Variazione della domanda al variare dei prezzi
mantenendo costante il potere d’acquisto (è
ancora possibile acquistare X1)
IL PARADOSSO DI GIFFEN
Visualizzato con il metodo delle variazioni compensative di reddito
QB
X2
X1
X3
QA
O
X1  X3 effetto sostituzione (+)
X1  X2
effetto prezzo
(-)
X2  X3 effetto reddito
bene inferiore
(-)
Il bene di Giffen è un bene
inferiore che presenta un
effetto reddito (-) così
forte da più che
compensare l’effetto
sostituzione (+); con il
risultato che una
diminuzione di prezzo
genera una diminuzione
della domanda del bene
(Paradosso di Giffen).
Questo produce un’ E pA
positiva, cioè una curva di
domanda rispetto al prezzo
inclinata positivamente
Curva di domanda
(abbiamo visto che è possibile derivarla dalla linea di prezzo consumo)
QB
PA1
pA
PA2 < PA1
PA1
PA2
PA3 < PA2
O
Q1
Q2 Q3
QA
PA3
Q1
Q2 Q3
QA
In questa rappresentazione la domanda del bene dipende dal suo prezzo
(operiamo con il metodo di analisi di equilibrio parziale, cioè ipotizziamo che tutte le altre grandezze
rilevanti rimangano invariate – coeteris paribus)
In generale la funzione di domanda può essere espressa come:
QA = f (pA, R, pB , pC , pD ,……)
(funzione di domanda Marshalliana)
Continuando ad operare attraverso analisi di equilibrio parziale, possiamo
studiare come varia la domanda di un bene rispetto:
1. Al prezzo del bene ferme restando tutte le altre variabili
QA = f (pA, R, pB , pC , pD ,……)
(Curva di domanda individuale e curva di domanda di mercato)
1
2
PA
Mercato
PA
PA
10
O
3
QA
O
2
QA
O
5
QA
2. Al reddito dell’individuo ferme restando tutte le altre variabili (funzioni di domanda Engeliane)
QA = f (R, pA, pB , pC , pD ,……)
3. Al prezzo di altri beni ferme restando tutte le altre variabili
QA = f (pB, pA, R, pC , pD ,……)
Un ruolo centrale nello studio delle varie funzioni di domanda è svolto
dal concetto di elasticità
In generale un indice di elasticità è un indice di variabilità relativa.
Ci informa cioè sulla variazione percentuale di una variabile indotta da una
variazione percentuale di un’altra
Problemi legati alle
variazioni assolute
X
prezzo
5
4
Y
mele (Kg)
3
5
Y = 13 - 2 x
d x/ x
nel caso di variazioni infinitesime
Y
mele (hg)
30
50
Y = 130 - 20 x
Data la funzione Y = f (x), l’indice di elasticità è:
d y /y
X
prezzo
5
4
Dy / y'
Dx / x'
Nel caso di variazioni finite, con y' e x'
pari alla media dei valori estremi
dell'intervallo di variazione
Essendo il rapporto di due variazioni relative (numeri puri) è a sua
volta un numero puro, che non dipende quindi dall’unità di misura
delle variabili
Attraverso l’indice di elasticità è possibile studiare le variazioni della quantità
domanda di un bene al variare delle variabili rilevanti
(1. prezzo del bene; 2. Reddito; 3. prezzo di altri beni)
1
L’ elasticità della domanda da prezzo
assume la seguente forma:
E pA = (d QA / QA)/( d pA / pA)
(elasticità puntuale - incremento infinitesimo)
E pA = D QA /[( QA1+ QA2)/2]/ D pA/[(pA1+ pA2)/2]
(elasticità di arco – incremento finito)
Determinazione geometrica dell’indice di elasticità puntuale
della domanda rispetto al prezzo
E pA = (d QA / QA)/( d PA / PA) = (d QA / d PA) * (PA / QA)
pA
D
L’elasticità diminuisce (in valore assoluto)
scendendo lungo la curva da X a X1
QA
O
B
Per una curva di domanda lineare (DB)
 = (-)  in D;
 = 0 in B
Per ogni curva di domanda i valori dell’elasticità assumo generalmente (ad esclusione che nel
caso dei beni di GIFFEN) valori negativi, compresi tra -  e 0.
Convenzionalmente, si parla però di elasticità in termini di valori assoluti
 > 1 domanda elastica;
 = 1 domanda ad elasticità unitaria;  < 1 domanda inelastica
Casi particolari delle funzioni di domanda di un bene, quando l’elasticità è costante
pA
O
pA
pA
QA
Elasticità infinita
O
QA
Elasticità zero
O
QA
Elasticità uno