trasparenze ppt

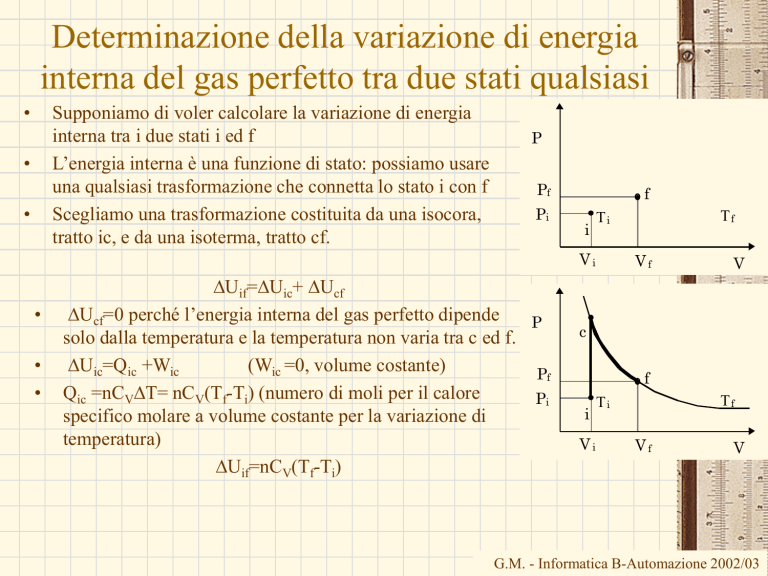
Determinazione della variazione di energia
interna del gas perfetto tra due stati qualsiasi
•
Supponiamo di voler calcolare la variazione di energia
interna tra i due stati i ed f
L’energia interna è una funzione di stato: possiamo usare
una qualsiasi trasformazione che connetta lo stato i con f
Scegliamo una trasformazione costituita da una isocora,
tratto ic, e da una isoterma, tratto cf.
•
•
P
Pf
Pi
f
i
Vi
•
•
•
DUif=DUic+ DUcf
DUcf=0 perché l’energia interna del gas perfetto dipende
P
solo dalla temperatura e la temperatura non varia tra c ed f.
DUic=Qic +Wic
(Wic =0, volume costante)
Pf
Qic =nCVDT= nCV(Tf-Ti) (numero di moli per il calore
Pi
specifico molare a volume costante per la variazione di
temperatura)
DUif=nCV(Tf-Ti)
f
i
Vf
V
c
f
i
Vi
f
i
Vf
V
G.M. - Informatica B-Automazione 2002/03
La relazione di Mayer
CV 
•
•
1 dU
n dT V
Per un gas perfetto
H=U(T)+nRT
CP 
1 dH
n dT P
dove H  U  PV
PV=nRT
(H(T))






1 dH
1 dU(T)  nRT 
1 
d U(T)

CP 


 nR  C V  R
n dT P n
dT
n 
dT P

P
Dato ch e U no n dipende da P

fare la derivata risp etto aT

pressio ne co stan te o a vo lume

acostante
è la stessa co sa
:


=C V
• Gas monoatomici
C
C R 5
3
5
  P  V
  1.6
CV  R  CP  R
C
C
3
2
2
V
V
•
Gas biatomici
5
7
CV  R  CP  R
2
2
 
CP C V  R 7

  1.4
CV
CV
5
G.M. - Informatica B-Automazione 2002/03
L’equipartizione dell’energia
N
U

i1




1
K i  N K  N m v2x  v2y  v 2z
  N K x  K y  K z
2
energia
è la so m ma dei v alori m edi 
lungo i tre assi, che p eraltro so no
cinetica
m edia
uguali.


Kx 

1
1
m v2x  kT
2
2
U  N Kx  Ky  Kz

k costante di Boltzmann
NA k = R

1
1  3
3
3
1
 N kT  kT  kT  NkT  nN A kT  nRT
2
2
2  2
2
2
3
1 dU 1 d2 nRT  3
CV 

 2R
n dT n dT
CP  CV  R  32 R  R  52 R
G.M. - Informatica B-Automazione 2002/03
Gas biatomici
•
•
•
•
I gradi di libertà di una molecola biatomica
3 di traslazione (x,y,z)
2 di rotazione (lungo i due assi perpendicolare
alla congiungente i due nuclei
2 di oscillazione (energia cinetica e potenziale)
7
7
U  N kT  n RT
2
2
7
1 dU 1 d2 nRT  7
CV 

 2R
n dT n dT
•
•
•
È come se ci fossero delle
soglie
Solo al di sopra di una certa
energia media si attivano i
gradi di libertà della rotazione e
quelli della oscillazione
Comportamento non spiegabile
con la meccanica classica
G.M. - Informatica B-Automazione 2002/03
•
•
Appli
cazio
ne
Una quantità di gas ideale monoatomico alla temperatura di 10.0°C e a una
pressione di 100 kPa occupa un volume di 2.50 m3. Il gas viene riscaldato a
volume costante fino a quando la pressione diventa 300 kPa .
Determinare il calore assorbito dal gas e la variazione di energia interna.
P
PV  nRT
N
100  10 2  2.50m 3
P1Vo
m
n

 106.2mol
J
RT1 8.314
273.15  10.0K
mol  K
3
P2
P1
Vo
N
300  103 2  2.50m 3
PV
m
T2  2 o 
 849.4K
J
nR
8.314
106.2mol
mol  K
W0
V
T
DU  Q
T+dT
3
J
DU  nC VDT  106.2mol   8.134
849.4  283.15K 
2
mol  K
 733.7kJ
G.M. - Informatica B-Automazione 2002/03
•
•
Una quantità di gas ideale biatomico alla temperatura di 0.0°C e a una pressione
di 100 kPa occupa un volume di .50 m3. Il gas viene riscaldato a pressione
costante fino a quando il volume raddoppia.
Determinare il calore assorbito dal gas, la variazione di energia interna, il lavoro
effettuato.
P
PV  nRT
N
3

.50m
2
PVi
m
n

 22.0mol
J
RT i 8.314
273.15K
mol  K
100  103
N
100  103 2  1.00m 3
PVf
m
Tf 

 546.7K
J
nR 8.314
22.0mol
mol  K
Appli
cazio
ne
P
Vi
Vf
V
W  PVf  Vi   100 10 Pa  1.00  .50  50kJ
3

5
J
DU  nC VDT  22.0mol   8.134
546.7  273.15K 
2
mol  K
d
 122.4kJ
7
J
Q  nC P DT  22.0mol   8.134
546.7  273.15K  171.4kJ
2
mol  K
G.M. - Informatica B-Automazione 2002/03
•
Appli
cazio
ne
Calcolate il lavoro svolto da un agente esterno durante una compressione
isoterma di una certa quantità di ossigeno da un volume di 22.4 L alla
temperatura di 0.00°C e 1 bar di pressione a un volume di 16.8L.
N
3 3

22.4

10
m
2
PVi
m
n

 0.99mol
J
RT i 8.314
273.15K
mol  K
105
P
Pf
Isoterma
Pi
W
dW  PdV

f
PdV 
i

f
i
nRT
dV   nRT
V

f
i
dV
V
 nRT logV i  nRT logV f  logV i   nRTlog
f

Vf
Vf
Vi
Vi
V
PV  nRT
Vf
J
16.8
W  nRTlog
 1mol  8.314
273.15Klog
 639.17J
Vi
molK
22.4
DU  0
DU  Q  W
QW
West  W  639.17J
G.M. - Informatica B-Automazione 2002/03
•
Una certa massa di gas occupa un volume di 4.3 L a una pressione di 1.2 bar e
una temperatura di 310 K.
Essa viene compressa adiabaticamente fino a un volume di 0.76 L.
Determinare la pressione finale e la temperatura finale supponendo che si tratti
di un gas ideale per il quale =1.4.
•
•
•
•
Dobbiamo innanzitutto determinare l’espressione di una adiabatica reversibile.
Troveremo infatti che l’adiabatica reversibile vale
PV  nRT

PV  cos t
•
Appli
cazio
ne
O una equazione che deriva da questa utilizzando l’equazione di stato

PV 
1

nRT 
 1
V  cos t  TV  cos t
V
P V P
1

nRT
 cost  TP
P
1
1

 cost
G.M. - Informatica B-Automazione 2002/03
Le trasformazioni del gas perfetto:
adiabatica
reversibile
•
P
Consideriamo un tratto infinitesimo di adiabatica
reversibile
dU  Q  W
Q  0
dU  nC V dT
W  PdV
Adiabatica
Pi
 dU  W
Pf
Vi
Vf
 nC VdT  PdV
nC VdT  
V
1
nRT
dV
V
CV
dT
dV

C P  CV T
V
dT
dV

CP
T
V
1
CV
1 dT
dV

 1 T
V
G.M. - Informatica B-Automazione 2002/03
Le trasformazioni del gas perfetto:
adiabatica
reversibile
P
1 dT
dV

 1 T
V
•
Adiabatica
Pi
Sommiamo su tutti i tratti infinitesimi

f
i
1 dT

 1 T

f
i
dV
V
1
Tf 1
Vi


log
 log
Ti 
Vf
 1
Tf Vf

 1
Ti Vi
1
T
V
log f  log f
 1
Ti
Vi
1
Tf  1 Vi
  
Ti 
Vf
Pf
Vi
Vf
V
 1
Tf 
Vi 



Ti Vf 
TV  1  cos t
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
Appli
cazio
ne
PV  nRT
Una certa massa di gas occupa un volume di 4.3 L a una pressione di 1.2 bar e
una temperatura di 310 K.
Essa viene compressa adiabaticamente fino a un volume di 0.76 L.
Determinare la pressione finale e la temperatura finale supponendo che si tratti
di un gas ideale per il quale =1.4.
L’ adiabatica reversibile vale


PV  cos t

Pf Vf  Pi Vi

1.4

V

4.3


5
  13.56bar
Pf Vf  Pi  i   1.2 10
0.76 
Vf 
 1
Tf Vf

 1
Ti Vi
Pi Vi  nRTi
Pf Vf  nRT f
1
Vi 
Tf  Ti  
Vf 
0.4
 4.3 
 310K
0.76 
 620K
Pf Vf
Tf  Ti
Pi Vi
13.56bar  0.76L
Tf  310K
 619.1K
1.2bar  4.3L
G.M. - Informatica B-Automazione 2002/03
•
•
In figura sono illustrate le quattro trasformazioni reversibili (isocora, isobara,
isoterma ed adiabatica) subite da una certa quantità di gas ideale.
Identificate le quattro trasformazioni e poi ordinatele
– secondo i valori decrescenti del calore assorbito dal gas
– secondo i valori decrescenti del lavoro effettuato dal gas
– secondo i valori decrescenti della variazione di energia interna
•
–
–
–
–
•
•
•
•
•
Secondo valori decrescenti del lavoro
effettuato (area al di sotto della
trasformazione)
1
2
3
4
Isobara
Isoterma
Adiabatica
Isocora
Secondo valori decrescenti della
variazione di energia interna
DU=nCVDT
– 1 Isobara
– 2 Isoterma
– 3 Adiabatica, 4 Isocora a pari
merito
•
Appli
cazio
ne
PV  nRT
1
2
3
4
Isobara
Isoterma
Adiabatica
Isocora
Secondo valori decrescenti del calore
assorbito Q= DU+W
–
–
–
–
1
2
3
4
Isobara (Q= DU+W)
Isoterma (Q=W)
Adiabatica, (Q=0)
Isocora
(Q<0)
G.M.
- Informatica B-Automazione 2002/03
L’adiabatica ha una pendenza più elevata
della isoterma passante per lo stesso stato


PV  Po Vo
PV  Po Vo
PV
P o o
V
Po Vo
P

V
per l' isoterma
per l' adiabatica
P
Po
Isoterma
dP
P
 1
 Po Vo  2    o
 V V
dV Vo
Vo
o
 1

dP

  V
 Po Vo  2  
dV Vo
 V 
Vo
•
•
•
•
 
Adiabatica
Vo
o
V
Po
Vo
Tutte e due le pendenze sono negative
L’adiabatica ha una pendenza che è  volte quella dell’isoterma
Ma  è maggiore di 1 (CP>CV)
La pendenza dell’adiabatica in valore assoluto è più grande di quella
dell’adiabatica
G.M. - Informatica B-Automazione 2002/03
•
Un gas monoatomico ideale, a una temperatura iniziale To (in Kelvin) si espande
da un volume Vo ad un volume 2Vo per mezzo di uno dei cinque processi indicati
nel grafico delle temperature in funzione del volume mostrato in figura.
– In quale processo l'espansione è
• isoterma
• isobara (pressione costante)
• adiabatica
Appli
cazio
ne
– Date una spiegazione alle vostre risposte.
•
•
Isoterma trasformazione AE
Isobara trasformazione AC
PVo  nRTo
P2Vo  nRT1

T1  2To
•
Adiabatica trasformazione AF
T1 2Vo 
 1
 1
 To Vo
 T1 
To
To

1
1.661  .63To
2
2
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
•
Un gas ideale subisce una compressione adiabatica reversibile da P=1.0 bar,
Appli
V=1.0 106 litri, T=0.0 °C a P= 1.0 105 bar, V=1.0 103 litri.
Si tratta di un gas monoatomico, biatomico o poliatomico?
cazio
Qual è la temperatura finale?
ne
Quante moli del gas sono presenti?
Qual è l’energia cinetica traslazionale per ogni mole prima e dopo la
compressione?


Pi
V

Pi
V


  f   log  log f
PiVi  PfVf
Pf Vi 
Pf
Vi
Pi
1
log
log 5
Pf
log105 5  log10 5
10
 



  1.66
Vf
103 log103 3  log10 3
log
log 6
Vi
10
Po Vo
105 Pa  10 3 m 3
• Il gas è monoatomico
Po Vo  nRT o  n 

 44000mol
RTo 8.31 J 273.15K
molK
PV
Tf  f f
nR
Tf  K 
101 0 Pa  1m 3
 Tf 
 27349K
J
8.31
44000mol
molK
3
kT 
2
Kmol  NA
3
3
3
kT  RT  8.31  273.15  3404J
2
2
2
G.M. - Informatica B-Automazione 2002/03