CAPITOLO 8
Le leggi della termodinamica
Il primo principio della termodinamica è fondamentalmente un’affermazione della conservazione dell’energia,
che include in modo specifico anche il calore. In un sistema con energia interna (somma di tutte le energie
potenziali e cinetiche) Ui se aggiungiamo calore Q avremo alla fine energia interna Uf seguendo la formula: Uf =
Ui + Q scritta anche come ΔU = Uf – Ui = Q. Q ha valore positivo quando il sistema acquista calore e valore
negativo quando lo cede.
Analogamente se un sistema compie un lavoro W sull’ambiente esterno avremo una variazione di energia interna
pari a Uf = Ui – W scritto anche come ΔU = Uf – Ui = – W. Il lavoro W ha valore positivo quando viene
eseguito dal sistema e valore negativo se il lavoro viene fatto sul sistema. Combinando i risultati otteniamo il
primo principio della termodinamica: ΔU = Q – W (variazione di energia interna = calore – lavoro).
L’energia interna dipende soltanto dallo stato del sistema e non da come il sistema è stato portato il quello stato:
per questo viene chiamata funzione di stato. Al contrario Q e W non sono funzioni di stato, ma se in un sistema
abbiamo una variazione di Q e di W la variazione di energia interna sarà sempre la stessa. ΔU = Q1 – W1 = Q2 –
W2.
Esaminando le trasformazioni termodinamiche dobbiamo supporre che esse siano processi quasi-statici, cioè
avvengono cosi lentamente che in ogni istante il sistema e l’ambiente circostante sono in equilibrio. La pressione
e la temperatura sono uniformi in tutto il sistema e non ci sono forze dissipative. I processi di questo tipo sono
detti reversibili: ovvero deve essere possibile sia per il sistema che per l’ambiente circostante ritornare
esattamente nello stesso stato in cui erano prima che la trasformazione iniziasse.
I processi reali sono quasi tutti irreversibili poiché è quasi impossibile eliminare tutte le forze di attrito.
Esaminando una trasformazione a pressione costante detta isobara, supponiamo che un gas sia contenuto in un
cilindro e il gas espandendosi compie lavoro sul pistone. Sapendo che il lavoro è F · s e la forza è la pressione per
l’area del pistone e lo spostamento è l’altezza dello spostamento del pistone possiamo dire che W = F(h) = PA(h).
Sapendo che l’altezza per l’area è il volume dello spostamento, ovvero la variazione di volume del cilindro,
possiamo scrivere W = PΔV. Da ciò deriva ΔU = Q – PΔV. In un grafico pressione-volume si formerà un linea
orizzontale che proiettata sull’asse delle ascisse formerà un’area che rappresenta il lavoro.
In una trasformazione a volume costante detta isocora il lavoro è pari a zero percui la variazione di energia
interna e uguale al calore ΔU = Q. In un grafico pressione-volume si formerà un linea verticale che non formerà
l’area che rappresenta il lavoro poiché non c’è lavoro.
In una trasformazione a temperatura costante detta isoterma il lavoro è pari alla formula W = NkT ln(Vf/Vi) o
nRT ln(Vf/Vi). Il lavoro è uguale a numero di molecole per costante di Boltzmann per temperatura per logaritmo
naturale del rapporto tra volume finale e iniziale oppure il lavoro è uguale a numero di moli per costante
universale dei gas per temperatura per logaritmo naturale del rapporto tra volume finale e iniziale. Nel grafico
pressione e volume si forma un arco di iperbole equilatera. In una isoterma il prodotto tra P e V è costante;
PV = costante. In una trasformazione isoterma ΔU = 0 e Q = W.
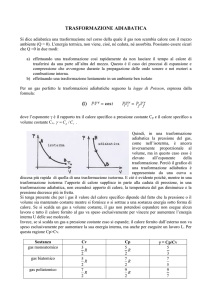
In una trasformazione adiabatica ovvero dove non c’è scambio di calore, perciò Q = 0 e ΔU = - W. La curva
nel grafico assomiglia ad un isoterma, ma è una curva più ripida. Una trasformazione adiabatica avviene solo
quando il sistema isolato oppure la variazione di volume è cosi rapida che il calore non viene ne assorbito ne
ceduto. In una trasformazione adiabatica vale il rapporto PVγ = costante. In una compressione adiabatica,
ovvero quando c’è diminuzione di volume, la pressione e la temperatura aumenteranno. In una espansione
adiabatica, ovvero quando c’è aumento di volume, la pressione e la temperatura diminuiscono.
Il calore specifico a volume costante segue la formula Q = m · c · ΔT (calore = massa per calore specifico per
variazione di temperatura). Utilizzando il calore specifico molare, indicato con la lettera maiuscola C, che è
definito utilizzando le moli di una determinata sostanza più che la massa, avremo la formula: Q = n · C · ΔT (
calore = numero moli per calore specifico molare per variazione di temperatura).
La stessa relazione può essere usata in una trasformazione a pressione costante. I calori specifici delle due
relazioni possono essere messi in relazione: attraverso la formula dell’energia interna troviamo che il calore
specifico molare a volume costante è Cv = 3/2R, mentre quello a pressione costante è Cp = 5/2R. DA ciò
possiamo individuare che Cp – Cv = R. Tutto ciò ci serve per ricavare la γ della relazione delle trasformazioni
adiabatiche: γ =Cp/Cv= 5/3. Questo valore di γ vale per i gas ideali e reali monoatomici, ma non per quelli non
monoatomici.
© Federico Ferranti S.T.A.
www.quartof.com