doc - INFN Roma1

Esercitazioni del 19/05/2010
Problema 1)
Quattro moli di gas perfetto monoatomico eseguono una trasformazione ciclica composta
da un’ espansione isoterma, una compressione isobara ed una trasformazione isocora.
Sapendo che la temperatura dell’ isoterma e’ TFe  320K e che durante l’ isobara il
volume si dimezza, calcolare:
1. il lavoro del ciclo
2. il calore scambiato nell’ isoterma
3. il calore scambiato nell’ isobara
Soluzione
P
A
C
B
V
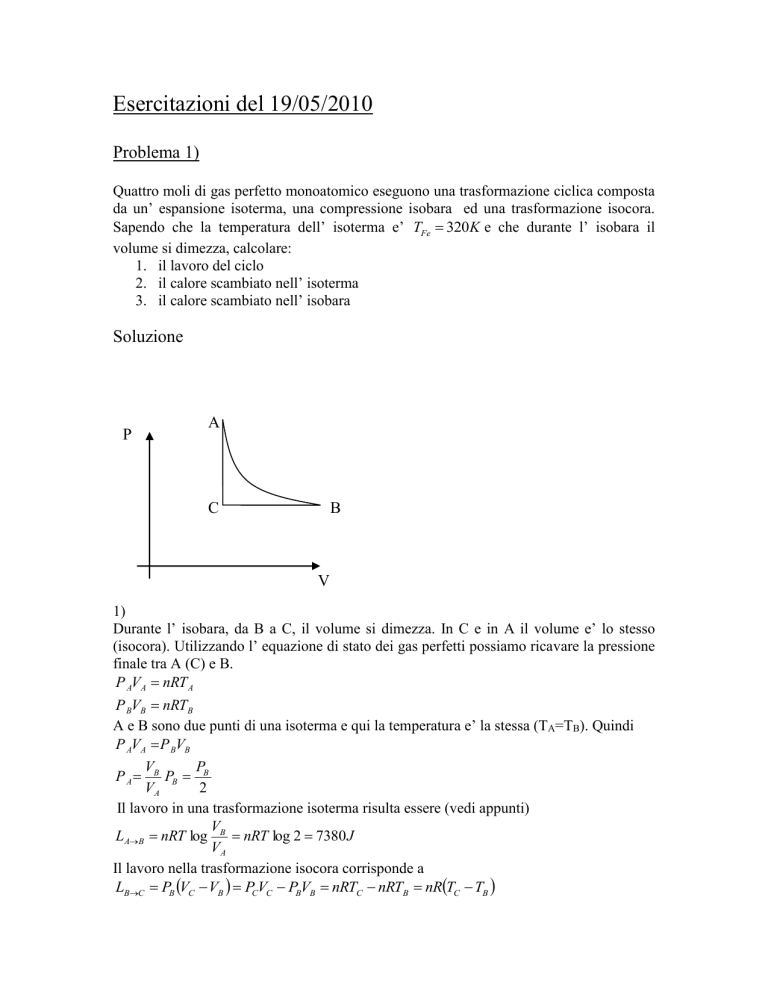
1)
Durante l’ isobara, da B a C, il volume si dimezza. In C e in A il volume e’ lo stesso
(isocora). Utilizzando l’ equazione di stato dei gas perfetti possiamo ricavare la pressione
finale tra A (C) e B.
P AVA  nRT A
P BVB  nRTB
A e B sono due punti di una isoterma e qui la temperatura e’ la stessa (TA=TB). Quindi
P AVA  P BVB
VB
P
PB  B
VA
2
Il lavoro in una trasformazione isoterma risulta essere (vedi appunti)
V
LAB  nRT log B  nRT log 2  7380 J
VA
Il lavoro nella trasformazione isocora corrisponde a
LBC  PB VC  VB   PCVC  PBVB  nRTC  nRTB  nRTC  TB 
P A
Dobbiamo calcolare la temperatura in C. Sempre dall’ equazione dei gas perfetti
P
(ricordandoci che VC  VA ; P C  PB  A ) abbiamo
2
P CVC  nRTC
PA
1
VA  nRT A
2
2
 TC  TA / 2  160 K
Quindi il lavoro corrisponde a
LBC  nRTC  TB   5320 J
P CVC 
Nella isocora il lavoro e’ nullo.
Nell’ intero ciclo abbiamo percio’
Lciclo  LAB  LBC  LC A  7380 J  5320 J  0  2060 J
2)
Dal primo principio sappiamo che
Q  L  U
In una trasformazione isoterma la temperatura e’ costante e quindi non vi e’ variazione di
energia interna
U AB  0
 QAB  LAB  7380 J
3)
Il calore scambiato in una isobara e’
QBC  ncP TC  TB 
dove (per un gas monoatomico)
3
5
cP  cV  R  R  R  R
2
2
Quindi otteniamo
5
QBC  n RTC  TB   13300 J
2
Problema 2)
Un blocco di ferro di massa mFe  900 g a temperatura TFe  10o C viene immerso in un
recipiente isolato termicamente contenente 2 litri d’ acqua a temperatura Tac  80o C . Si
calcoli la temperatura finale dell’ acqua e del ferro i cui calori specifici sono:
cac  4186 J /( kgK ) e cFe  444 J /( kgK )
Soluzione
All’ equilibrio acqua e ferro hanno la stessa temperatura che viene raggiunta scambiando
calore. Poiche’ le pareti del recipiente sono isolanti il sistema e’ isolato termicamente e il
calore ceduto dall’ acqua deve essere uguale (a meno di un segno) a quello che acquisito
dal ferro.
Il calore nei due casi vale
Qac  cac mac (T f  Tac )
QFe  cFemFe (T f  TFe )
Imponendo dunque che i due calori siano uguali in modulo e opposti in segno abbiamo
Qac  QFe
cac mac (T f  Tac )  cFemFe (T f  TFe )
da cui
T f (cac mac  cFemFe )  cFemFeTFe  cac macTac
che da’
c m T c m T
T f  Fe Fe Fe ac ac ac  77 0C
cac mac  cFe mFe
Problema 3) (casa)
Si consideri un gas contenuto in un cilindro chiuso da un pistone mobile di sezione
S=40cm2. Il cilindro e’ un buon conduttore termico e si trova in un ambiente a
temperatura T=200C e pressione p0=1,013 105 Pa. Inizialmente sul pistone e’ posto un
blocco di massa M=1.2kg e il pistone si trova ad un’ altezza h=8cm dal fondo del
cilindro. Successivamente il gas compie il seguente ciclo: 1) la massa M viene tolta ed il
gas si espande raggiungendo l’ equilibrio termico; 2) la massa viene rimessa sul pistone,
il gas viene compresso e ritorna nello stato iniziale. Si calcoli il calore scambiato nel
ciclo.
Soluzione
Il ciclo e’ fatto da due trasformazioni, entrambe a pressione costante. Si tratta di
trasformazioni irreversibili. Il lavoro per una trasformazione a pressione costante si
calcola come
L  PV1  Vi 
Nella prima espansione la pressione e’ quella atmosferica. Nella compressione invece
essa corrisponde alla pressione atmosferica con l’ aggiunta della pressione dovuta alla
forza peso della massa M. Quindi
L1  P0 V1  Vi 
L2  P0  Mg / S Vi  V1 
La variazione di volume si calcola dall’ equazione dei gas perfetti. Infatti il cilindro e’ un
buon conduttore e dopo la prima trasformazione il sistema sara’ di nuovo alla
temperatura iniziale. Percio’
P0  Mg / S Vi  nRT
da cui
P 0V1  nRT
V 1 P0  Mg / S Vi / P0  Sh  Mgh / P0
Quindi il lavoro risulta valere
L1  P0 V1  Vi   Mgh
Per il secondo tratto
M 2 g 2h
L2  P0  Mg / S Vi  V1    Mgh 
P0 S
Nel ciclo dunque abbiamo
M 2 g 2h
Lciclo  L1  L2  
P0 S
La temperature finale e’ uguale a quella iniziale quindi la variazione di energia interna e’
nulla ( U  0) . Dal primo principio otteniamo
U ciclo  0
 Qciclo  Lciclo  
M 2 g 2h
 0.027 J
P0 S
Questo lavoro (negativo) coincide con il lavoro fatto dalla forza peso (Lext) per spostare la
massa dalla quota h alla quota h’ cambiato di segno.