Diapositiva 1

La termodinamica
Meccanica
Forze conservative, principio di conservazione dell’energia meccanica.
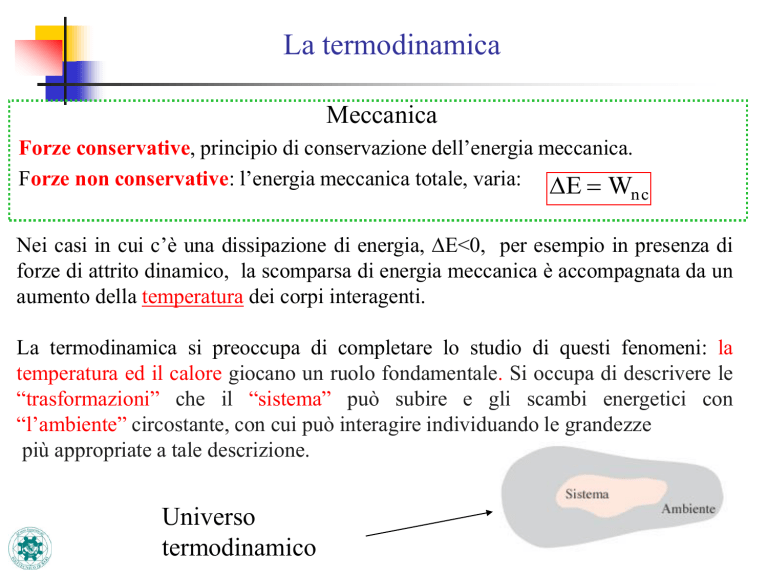
Forze non conservative: l’energia meccanica totale, varia: E  W
nc
Nei casi in cui c’è una dissipazione di energia, E<0, per esempio in presenza di
forze di attrito dinamico, la scomparsa di energia meccanica è accompagnata da un
aumento della temperatura dei corpi interagenti.
La termodinamica si preoccupa di completare lo studio di questi fenomeni: la
temperatura ed il calore giocano un ruolo fondamentale. Si occupa di descrivere le
“trasformazioni” che il “sistema” può subire e gli scambi energetici con
“l’ambiente” circostante, con cui può interagire individuando le grandezze
più appropriate a tale descrizione.
Universo
termodinamico
1
Le proprietà dei corpi solidi
Corpo solido   corpo rigido
I solidi sottoposti a sollecitazioni (normali o tangenziali alla superficie)
subiscono piccole deformazioni.
 Il fatto che le deformazioni siano piccole dipende dalla struttura cristallina e
dalle forze intermolecolari, che mantengono gli atomi nella loro posizione
all’interno del reticolo. Queste forze molto intense, simili a delle molle, sono in
grado di sviluppare una forza di reazione tale da equilibrare la forza applicata.

Gli atomi sono in continua oscillazione attorno alla posizione di equilibrio
 Con una ampiezza che dipende dalla temperatura
 È l’intensità elevatissima tra gli atomi che fa rassomigliare i solidi a corpi
rigidi.

2
I fluidi: gas e liquidi



le distanze intermolecolari sono in media più grandi nel caso dei fluidi rispetto ai solidi:

le forze di interazione sono estremamente meno intense: nei fluidi le molecole sono
debolmente legate l’una all’altra. La maggior parte dei fluidi sono incomprimibili.

esse non occupano posizioni predeterminate all’interno del fluido, ma possono
muoversi al suo interno.
I fluidi non oppongono alcuna resistenza a sollecitazioni di taglio

Se suddividiamo in due parti il fluido con una superficie ideale è possibile far
scorrere le due parti di fluido l’una rispetto all’altra (Si immagini la lama di un
coltello che scorre all’interno di un fluido.) Il fluido si adatta alla forma del
recipiente in cui viene a trovarsi.
Conseguenza:

Se separiamo il fluido in due parti mediante una superficie
qualsiasi le forze che una parte di fluido esercita sull’altra
hanno solo la componete normale alla superficie.
3
La pressione



Sulla superficie immaginaria con cui abbiamo suddiviso il fluido in due parti
prendiamo una piccola area, A, attorno al punto P

Sia A il vettore di modulo pari all’area superficiale DA e direzione
orientata per convenzione normalmente alla superficie verso l’esterno.
Si definisce pressione idrostatica nel punto P la grandezza scalare attenuta
facendo il rapporto della forza (normale) che una delle due parti di fluido
esercita sull’altra attraverso l’area A, diviso per l’area A (eventualmente si
fa il limite per A che tende a zero) :


 
F  pA  poichè Fe A sono //
F
p
A
4
Pressione: unità di misura
P  Fn A1  MLT 2L2 
• Le unità di misura nel SI sono N/m2, il “pascal”, Pa.
• Altre unità di misura della pressione:
– Atmosfera (atm) =1 atmosfera è la pressione atmosferica al livello del
mare
– torr (o mm Hg) è la pressione che esercita una colonna di 1 mm di
mercurio
– 1 bar = 105 Pa
5
1atm 1.013 10 Pa  760torr
5
Caratterizzazione di un Sistema Termodinamico
Sistema aperto: se tra il sistema e l’ambiente avvengono scambi di energia e
materia. Es. liquido in ebollizione ed il recipiente contenente il liquido,
dall’atmosfera e sorgente di calore.
Sistema chiuso: se tra il sistema e l’ambiente avvengono scambi di energia e non
di materia. Es. liquido in ebollizione ed il recipiente chiuso a contatto con sorgente.
Sistema isolato: se tra il sistema e l’ambiente non avvengono scambi né energia né
di materia.
Per studiare il comportamento di un sistema termodinamico dobbiamo
imparare a descriverlo:
microscopico
macroscopico
6
Caratterizzazione di un Sistema Termodinamico

Punto di vista microscopico: può essere studiato come un sistema di particelle.
 Si descrive il comportamento di ciascuna molecola (posizione, velocità,
energia cinetica, quantità di moto, etc). Leggi di Newton: le forze, interne
ed esterne agenti su ciascuna particella.
 è necessario un numero molto grande di grandezze per descrivere il
comportamento del sistema: che non hanno niente a che vedere con le
nostre percezioni sensoriali e che sono difficili da misurare direttamente

Punto di vista macroscopico
 Basato su grandezze, variabili termodinamiche, che descrivono il sistema
nel suo insieme, medie di caratteristiche microscopiche!!
 Non viene fatta alcuna ipotesi sulla struttura interna del sistema
 Generalmente sono in numero limitato
 Sono suggerite dai nostri sensi e sono misurabili direttamente
7
Equilibrio termodinamico
 Lo stato termodinamico di un sistema è detto di equilibrio quando le variabili
termodinamiche che lo descrivono sono costanti nel tempo, cioè non cambiano
fino a che non cambiano le condizioni esterne.
 Il numero minimo per descrivere per descrivere completamente il sistema non è
fissato a priori e dipendono dal sistema. In molti casi sono sufficienti due sole
coordinate termodinamiche X e Y per descrivere lo stato di un sistema
 Quando le condizioni esterne cambiano le coordinate termodinamiche, possono
cambiare. Il comportamento di un sistema termodinamico dipende dal tipo di
interazione che può avere con l’ambiente esterno.
 Adiabatiche: le coordinate termodinamiche del sistema non cambiano al
cambiare delle condizioni esterne
 Conduttrici. le coordinate termodinamiche del sistema variano, ma dopo un
tempo più o meno lungo, il sistema raggiunge un nuovo stato caratterizzato
da nuove coordinate termodinamiche che rimangono costanti fino a che non
cambino nuovamente le condizioni esterne.
8
Equilibrio termodinamico



Si dirà che il sistema si trova in equilibrio termodinamico, se esso si trova
contemporaneamente in:

equilibrio meccanico, quando non esistono forze o momenti non equilibrati né
all'interno del sistema, né tra il sistema e l'ambiente circostante.
 la pressione deve essere la stessa in tutte le parti del sistema e, se il contenitore
non è rigido, essa è la stessa dell’ambiente circostante.

equilibrio termico, quando tutte le parti del sistema hanno la stessa temperatura, e
se le pareti che circondano il sistema sono conduttrici, questa coincide con quella
dell'ambiente circostante.

equilibrio chimico, quando non avvengono processi che tendono a modificare la
composizione del sistema, come reazioni chimiche, né spostamenti di materia da
una parte all'altra del sistema, come accade per esempio quando una sostanza entra
in soluzione o quando una sostanza cambia fase, per esempio da liquido a vapore.
Noi riusciamo a descrivere solo gli stati di equilibrio termodinamico.
In uno stato di non equilibrio termodinamico la pressione può variare da punto a punto.
Non è possibile descrivere gli stati che non siano di equilibrio!
9
Principio dell’equilibrio termico
 Il concetto di temperatura ha origine dalla sensazione di caldo e freddo
che proviamo toccando un corpo.
Per darne un carattere obiettivo è necessario individuare una grandezza
fisica che esprima una proprietà macroscopica del corpo e che dipenda in
modo univoco dal suo stato termico. Il volume, la pressione..etc.
 Dati due sistemi A alla temperatura TA e B TB,
ciascuno in equilibrio termodinamico, si dicono in
equilibrio termico se hanno la stessa temperatura.
 Due sistemi in equilibrio termico con un terzo
sistema, sono in equilibrio termico tra loro:
principio zero della termodinamica.
A
B
A
B
C
10
Scale di temperatura
 Se A e B sono in equilibrio termico per un termometro lo sono per
qualunque altro termometro.
 Questo non è vero per la temperatura: ogni termometro definisce una sua
scala, misura una temperatura diversa.
La scala di temperature universalmente adottata è la scala kelvin. Basata
sull’assunzione che esiste un limite inferiore: temperatura dello zero
assoluto.
Per definire quanto valga 1 K occorre identificare un metodo di taratura,
un campione cui si assegna una determinata temperatura.
“1954, Conferenza dei Pesi e Misure”: punto triplo dell’acqua,
T0=273.16 K (esatto per convenzione) quel particolare stato in
cui ghiaccio, acqua e vapor saturo sono in equilibrio.
11
Le scale Celsius e Fahrenheit





La scala Celsius ha si basa su due
punti di taratura: il punto di
congelamento 0°C e di ebollizione
100 °C.
La relazione tra le due temperature è
la seguente: t C  T  273.15
L’unità di misura della scala
Celsius, 1°C, è uguale al campione
della scala Kelvin, 1 K.
1°C = 1K


La scala Fahrenheit fa coincidere
al punto di fusione dell’acqua la
temperatura tf = 32°F, e a quello di
ebollizione la temperatura di tf=
212°F
La relazione tra temperatura
Fahrenheit e centigrada è data da
t F  32 
212  32
9
tC  32  tC
100
5
Esiste solo un offset tra le due scale
0°C  273.15 K.
Dove tc temperatura in gradi Celsius e T temperatura in K (kelvin)
12
Definizione operativa di temperatura: termometri
 Scegliamo una sostanza termometrica: mercurio, elio, alcool.
 sia X la grandezza che descrivi la proprietà della sostanza che vari con la
temperatura: es. la lunghezza della colonna, la pressione
 sia T la funzione termometrica, assumiamo lineare:
T=aX
con a cost.
 Taratura del termometro: serve un sistema in equilibrio
definibile con precisione e riproducibilità cui venga attribuito
un valore arbitrario di temperatura: punto fisso, il punto triplo
dell’acqua, T0=273.16 K
T 0 = a X0
T = T0 /X0 X = 273.16 X/X0
Contatto
termico
Tuttavia a non è effettivamente lineare: bisogna individuare una
grandezza X che lo sia effettivamente.
13
Termometro a gas a volume costante
Termometri a gas a volume constante la
grandezza termometrica è la pressione del gas.
Livello di
riferimento
p
T  273.16
ptr
1. Posti n1 moli di gas nel bulbo, si
determinano le p, ptr e la T1
La pressione del gas è
misurata dal dislivello h
2. Posti n2 < n1 moli di gas nel bulbo,
si determinano le p, ptr , minori
perché p = n RT/V
Serbatoio di mercurio
14
Termometro a gas a volume costante
Temperatura vs della Pressione
del gas.
Varia linearmente con P in modo
differente a seconda del gas.
 p  0 è lo stesso per tutti i gas
I termometri a gas a volume costante, la differenza di T tra un termometro e
l’altro sono tanto più piccole quanto più il gas è rarefatto.
Scala di temperatura del termometro a gas perfetto
Tgas perfetto  lim
Ptr 0
P
273.16 K
Ptr
15
Dilatazione Termica


I corpi si dilatano con la temperatura. Esistono termometri che basano il loro
funzionamento sulla differenza di dilatazione tra i vari componenti.
I corpi unidimensionali (un filo, una sbarra, etc), per T piccoli:
   T
1d

dT
Coefficiente di dilatazione lineare
Dipende dalla temperatura, per intervalli limitati di T può essere considerato costante
16
La dilatazione superficiale e di volume
Consideriamo una lastra rettangolare, di un materiale isotropo (ossi che abbia il
coefficiente uguale in tutte le direzioni), entrambe le dimensioni si dilateranno
con la stessa legge:
1   T
'  1  T
A'  ' '  1   T  1   T 
1 2 T   T 
'1 
2
1
2
1
1 2
1
2
1
2
2
2
2

A'  A 1  2 T

Trascurando 2T2 rispetto a 2T
In maniera analoga si può vedere che il coefficiente di dilatazione
cubica è tre volte quella lineare

V'  V 1 3 T

3
1
2
17
Dilatazione di volume dei liquidi

Nel caso dei liquidi non è possibile parlare di dilatazione lineare o
superficiale

Si parla solo di dilatazione di volume, o cubica:

I valori del coefficiente di dilatazione di volume per i liquidi sono più
grandi, circa un fattore 10, dei corrispondenti valori per i solidi
(legame molecolare più debole)
b (K )
materiale
abbastanza indipendente dalla T.
acqua
1.8 10
b generalmente > 0 (se T aumenta e V anche)
Alcol etilic o 10.4 10
benz ina
9.6 10
la densità diminuisce
V  b VT
-1



-4
-4
-4
clorofo rmi o
glicerina
mercurio
14.0 10-4
5.3 10-4
1.8 10-4
18
Dilatazione di volume dell’acqua

L'acqua ha un comportamento diverso dagli altri liquidi.
 Tra 0°C e 4 °C ha un coefficiente di dilatazione negativo
 T aumenta e V diminuisce  la densità aumenta raggiungendo il
valore massimo a 4 °C.
 Per la temperatura al di sopra dei 4 °C l'acqua si dilata anche se non
in maniera lineare (T aumenta – V aumenta – la densità diminuisce).
 Quando i fiumi si raffreddano, l’acqua più fredda, a densità
maggiore scende verso il fondo, spingendo in superficie l’acqua
sottostante che a sua volta si raffredda.
 A 4 °C la densità diminuisce al diminuire di T; l’acqua fredda resta
in superficie ed inizia a solidificare (a 0°C). L’acqua sul fondo del
fiume non scende mai al di sotto dei 4° C.
19
Equazione di stato del gas perfetto
 I gas tendono ad uno stesso comportamento quanto più la pressione è
bassa e la temperatura è alta rispetto a quella di condensazione: gas perfetti
Legge di Avogadro: volumi uguali di gas nelle stesse condizioni di
pressione e temperatura contengono lo stesso numero di molecole.
 Legge di Boyle
PV = cost
T, N cost
 Legge di Charles, GayLussac: Vt = V0bT
p, N cost
Dove T è in K
20
Equazione di stato del gas perfetto
VN
1
V
p
V T
p, T cost
N, T cost
pV  NkT
Equazione di stato dei
gas perfetti
N, p cost
N: numero di molecole contenute nel V e k=1.3810-23 J/K è la cost. di Boltzmann
Se n: numero di moli (rapporto fra la massa espressa un grammi ed il peso
molecolare).
1 mole di qualsiasi sostanza contiene Na = 6.02 1023 molecole, Numero di
Avogadro
pV  nN a kT  nRT
litri  atm
joule
cal
R: costante
R  0.08205
 8.314
 1.986
mole  K
mole  K
mole 21K
universale dei gas
Applicazione
Una massa m = 5 10-3 di idrogeno è contenuta in un volume V = 100 l
alla temperatura di 20°C. Calcolare quanto vale la pressione. Quale
massa di ossigeno produce lo stesso risultato?
1mole H ha massa 2 10-3 Kg
3
510
n
 2.5moli
3
210
RT 2.5  8.34  293
4
pn


6
.
0910
Pa
1
V
10
2.5moli O  m  2.5  3210-3  80 103 Kg
22