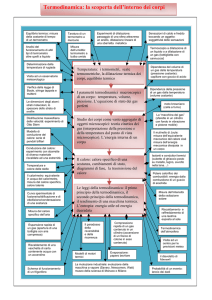
TERMODINAMICA
SISTEMI TERMODINAMICI
Il sistema è il corpo o l’insieme dei corpi sotto esame.
L’ambiente esterno è l’insieme di tutti i corpi che possono
interagire con il sistema.
Tipi di sistemi termodinamici
Un sistema termodinamico è detto:
aperto se è in grado di scambiare sia energia che materia con
l’ambiente esterno;
chiuso se si possono verificare scambi di energia, ma non di
materia, con l’ambiente;
isolato se non si verificano scambi né d’energia, né di materia
con l’ambiente.
PARAMETRI DI STATO
Non è possibile descrivere il comportamento di un sistema
macroscopico (costituito da un grandissimo numero di
componenti microscopiche) specificando lo stato di moto di
ciascuno dei suoi componenti microscopici.
Un sistema macroscopico viene descritto ricorrendo a
grandezze macroscopiche d’insieme che descrivono
caratteristiche del sistema nel suo complesso. Tali grandezze
sono dette parametri di stato o variabili termodinamiche
(volume, pressione, massa volumica, temperatura ecc.).
Lo stato di un sistema termodinamico è definito quando i
valori dei parametri di stato sono univocamente determinati.
TEMPERATURA, CALORE ED EQUILIBRIO TERMICO
La temperatura è una grandezza correlata all’energia cinetica
media di un sistema.
In particolare, per un gas a bassa pressione (gas ideale):
< Ek > =
3
kT
2
dove k è la costante di Boltzmann e T la temperatura in kelvin
(vedi in seguito).
Si considerino due sistemi A e B, come in figura, posti
inizialmente a temperature TA e TB, rispettivamente (con TA <
TB).
Finché i sistemi sono separati da una parete adiabatica (caso
a) le loro temperature non cambiano.
Se la parete adiabatica viene rimossa o sostituita con una
parete diatermica (caso b), dopo un adeguato tempo A e B si
portano entrambi ad una stessa temperatura T (TA < T < TB).
Una volta raggiunta questa situazione si dice che i due sistemi
sono in equilibrio termico.
Se due corpi a diversa temperatura vengono messi a contatto,
il corpo più caldo cede calore al più freddo.
Il calore è l’energia scambiata da due corpi (o tra due parti
dello stesso corpo) a causa della loro diversa temperatura.
Quando due sistemi sono in equilibrio termico, tra di essi
non si verifica nessuno scambio netto di energia sotto
forma di calore.
Il calore può trasformarsi in energia meccanica, così come
l’energia meccanica può trasformarsi in calore.
La termodinamica studia i fenomeni nei quali si verificano
trasformazioni di calore in altre forme di energia, oppure le
trasformazioni inverse.
Principio zero della termodinamica:
Due sistemi interagenti fra loro, ma isolati dall’ambiente
esterno, si portano all’equilibrio alla stessa temperatura.
oppure:
Due sistemi sono in equilibrio termico se, e solo se, sono
uguali le loro temperature.
Siccome potrebbe risultare difficoltoso, se non impossibile,
mettere due sistemi A e B a contatto termico tra loro, si ricorre
ad un terzo sistema C.
Se ciascuno dei due sistemi A e B è in equilibrio termico con
C, allora A e B sono in equilibrio termico tra loro.
MISURA DELLA TEMPERATURA E
SCALE TERMOMETRICHE
Scala Celsius (o centigrada)
Il metodo di taratura si attua assegnando per convenzione i
valori:
T = 100 °C
alla temperatura dell’acqua pura al punto di ebollizione in
atmosfera standard;
T = 0 °C
alla temperatura dell’acqua pura al punto di congelamento in
atmosfera standard.
In linea di principio il termometro misura una qualunque
grandezza X che dipende dalla temperatura (l’altezza di una
colonna di liquido, la resistenza elettrica di un conduttore, la
pressione di un gas, ecc.).
Il procedimento di misura si attua in due stadi:
1) Si pone il termometro in equilibrio termico con acqua pura
prima al punto di ebollizione e poi al punto di congelamento,
misurando i due valori X100 e X0, rispettivamente.
2) Si pone il termometro in equilibrio termico con il corpo di
cui si vuole determinare la temperatura, misurando per la
grandezza termometrica il valore X.
Assumendo una dipendenza lineare della grandezza
termometrica dalla temperatura, ossia:
X=aT+b
(1)
si ha:
X 0 = b
X 100 = 100 a + X 0
da cui:
b = X 0
X 100 − X 0
a
=
100
Introducendo questi valori nella (1), si ha infine:
T = (100
X − X0
) °C
X 100 − X 0
Nota: metodo scomodo poiché dipende dalla sostanza
utilizzata nel termometro e presuppone una relazione lineare
tra la grandezza termometrica e la temperatura.
Scala Fahrenheit
Il metodo di taratura si attua assegnando per convenzione i
valori:
T = 212 °F
alla temperatura dell’acqua pura al punto di ebollizione in
atmosfera standard;
T = 32 °F
alla temperatura dell’acqua pura al punto di congelamento in
atmosfera standard.
Il procedimento di misura è analogo a quello per i termometri
tarati in scala centigrada.
La relazione tra il valore della temperatura in gradi Fahrenheit
(TF) e quello in gradi centigradi (TC) è:
TF =
9
TC + 32
5
Scala Kelvin
Si definisce punto triplo, quella particolare configurazione
fisica dell’acqua pura in cui le sue tre fasi di aggregazione
(solida, liquida e aeriforme) coesistono in equilibrio.
Per convenzione si assegna alla temperatura dell’acqua pura al
punto triplo in atmosfera standard l’esatto valore T = 273.16 K
Il procedimento di misura si attua in due stadi:
1) Si pone il termometro in equilibrio termico con acqua pura
al punto triplo, misurando il valore Xtr.
2) Si pone il termometro in equilibrio termico con il corpo di
cui si vuole determinare la temperatura, misurando per la
grandezza termometrica il valore X.
Assumendo una proporzionalità diretta tra la grandezza
termometrica e la temperatura, ossia:
X=cT
si ha:
Xtr = 273.16 c
da cui:
T = (273.16
X
)K
X tr
(2)
Un corpo ha una temperatura assoluta di 1 K quando la sua
temperatura è 1/273.16 della temperatura dell’acqua al punto
triplo.
La temperatura del ghiaccio fondente (ossia la temperatura
del punto di congelamento dell’acqua) è pari a 273.15 K.
La relazione tra il valore della temperatura in gradi centigradi
e quella assoluta in kelvin (T) è:
TC = T – 273.15
In base a questa relazione si ottengono i seguenti valori.
Temperatura del punto di congelamento dell’acqua pura alla
pressione atmosferica standard: TC = 0.00 °C
Temperatura del punto di ebollizione dell’acqua pura alla
pressione atmosferica standard: TC = 99.975 °C
Temperatura dello zero assoluto: TC = – 273.15 °C
Nota importante
∆T = 1 °C ⇔ ∆T = 1 K ⇔ ∆T = 1.8 °F
DILATAZIONE TERMICA
Si chiama dilatazione lineare l’aumento di qualsiasi
dimensione lineare di un solido, come la lunghezza, la
larghezza o lo spessore.
Indicando con L la lunghezza di questa dimensione lineare, la
variazione di temperatura ∆T provoca una variazione di
lunghezza ∆L data da:
∆L = α L ∆T
Il coefficiente di dilatazione lineare α assume valori
caratteristici che variano da sostanza a sostanza.
A rigore α varia con la temperatura (ma è in buona
approssimazione costante per solidi e liquidi).
Per la maggior parte delle sostanze solide (isotrope) α è
uguale in tutte le direzioni entro il corpo.
Per un fluido il coefficiente di dilatazione lineare è privo di
significato. Per qualunque corpo (solido o fluido) è invece
possibile definire un coefficiente di dilatazione volumica β,
tale che la variazione di volume ∆V è:
∆V = β V ∆T
con V volume iniziale del corpo.
Per i solidi isotropi:
β = 3α
Tipicamente risulta:
β(gas) ≈ 10 β(liquido) ≈ 100 ÷ 1000 β(solido)
In genere si ha che β > 0, ossia i corpi si dilatano
all’aumentare della temperatura.
Comportamento anomalo dell’acqua.
Al contrario dei liquidi, i gas hanno un coefficiente di
dilatazione volumica fortemente dipendente dalla temperatura.
Fondamenti microscopici della dilatazione termica
Il motivo della dilatazione termica di un solido cristallino
risiede nella forma asimmetrica della curva che descrive
l’energia potenziale di una coppia di atomi adiacenti.
All’aumentare della temperatura l’energia vibrazionale aumenta e ciò
implica un aumento della distanza interatomica: il solido si dilata.
Anche in un fluido, all’aumentare della temperatura e quindi
dell’agitazione termica, la distanza interatomica media
aumenta.
EQUAZIONE DI STATO DEL GAS PERFETTO
Si definisce gas perfetto o ideale un gas le cui proprietà
rappresentano il comportamento limite dei gas reali quando la
loro massa volumica tende a zero.
Per i gas perfetti esiste la seguente relazione empirica tra
pressione p, volume occupato V, numero di molecole N e
temperatura assoluta T (equazione di stato del gas perfetto):
pV=NkT
(3)
dove k = 1.38 × 10−23 J/K è la cosiddetta costante di
Boltzmann.
Introducendo il numero di Avogadro NA (numero di molecole
contenute in una mole di qualsiasi sostanza, pari a 6.02 × 1023)
si ha:
N = n NA
(n numero di moli contenute nel gas)
p V = n NA k T = n R T
(3′)
dove R = k NA è detta costante molare dei gas.
La (3) e la (3’ ), rigorosamente valide per gas perfetti,
descrivono spesso in ottima approssimazione anche le
proprietà dei gas reali a bassa densità.
L’equazione di stato racchiude in sé diverse leggi,
precedentemente trovate da vari scienziati, che mettono in
evidenza le relazioni esistenti tra due variabili quando si
mantengono costanti le altre due. In particolare:
1) Sotto le medesime condizioni di pressione e temperatura,
uguali volumi di gas diversi contengono lo stesso numero di
molecole: V ∝ N, per p e T costanti.
(Legge di Avogadro)
2) Mantenendo costante il numero di molecole e la
temperatura di un gas, la pressione è inversamente
proporzionale al volume occupato: p ∝ V−1, per N e T
costanti.
(Legge di Boyle-Mariotte)
3) Mantenendo costante il numero di molecole e la pressione
di un gas, il volume occupato è direttamente proporzionale
alla temperatura: V ∝ T, per N ed p costanti.
(Prima legge di Gay-Lussac o Legge di Charles)
4) Mantenendo costante il numero di molecole ed il volume di
un gas, la pressione è direttamente proporzionale alla
temperatura: p ∝ T, per N ed V costanti.
(Seconda legge di Gay-Lussac)
IL TERMOMETRO A GAS A VOLUME COSTANTE
L’equazione di stato del gas perfetto indica che la proprietà
termometrica che si dimostra più adatta per le misure di
temperatura sulla scala Kelvin è la pressione p di un gas
mantenuto a volume fissato.
Il dispositivo per tale misura è il cosiddetto termometro a gas
a volume costante (v. figura).
Stante la proporzionalità diretta tra p e T stabilita dalla (3), si
può utilizzare la (2) con X = p e Xtr = ptr.
Finché il gas nel bulbo ha densità relativamente alta:
a) per uno stesso gas, al variare di ptr (ossia la variare della
densità), si misurano valori leggermente diversi per la
temperatura dello stesso corpo;
b) cambiando il gas, per lo stesso valore di ptr si misurano di
nuovo valori leggermente diversi per la temperatura dello
stesso corpo.
Al diminuire della densità, la temperatura del corpo tende allo
stesso valore, indipendentemente dalla densità del gas e dal
tipo di gas.
Si può concludere che la temperatura “effettiva” del corpo è
data da:
T = (273.16) lim ptr → 0
p
ptr
Con qualunque gas, a qualunque densità (sufficientemente
bassa), la temperatura è sempre la stessa.
La minima temperatura misurabile con questo strumento è di
circa 1 K (si usa elio a bassa pressione).