Fisica
Facoltà di Ingegneria, Architettura e delle
Scienze Motorie
Lezione 2 maggio 2013
Architettura
(corso magistrale a ciclo unico quinquennale)
Prof. Lanzalone Gaetano
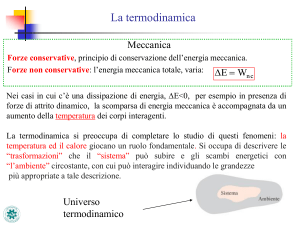
La termodinamica
•
Nello studio della meccanica abbiamo lasciato alcuni problemi aperti
– L’energia meccanica totale in presenza di forze non conservative, varia
ΔE = Lnc
•
Nei casi in cui c’è una dissipazione di energia, ΔE<0, – per esempio in presenza di forze di attrito dinamico, – la scomparsa di energia meccanica è accompagnata da un aumento della temperatura
dei corpi interagenti.
•
La termodinamica si preoccupa di completare lo studio di questi fenomeni – in questo studio la temperatura gioca un ruolo fondamentale.
•
Quindi dobbiamo studiare le interazioni – di un sistema – con l’ambiente circostante
•
La termodinamica studia ciò
Superficie ideale, o reale,
che succede all’interno del sistema.
che separa il sistema
dall’ambiente circostante
Ambiente circostante
Sistema
Descrizione macroscopica e microscopica
Per studiare il comportamento di un sistema termodinamico dobbiamo imparare a descriverlo
•
•
Punto di vista macroscopico
– Basato su grandezze, coordinate
termodinamiche, che descrivono il
sistema nel suo insieme
– Non viene fatta alcuna ipotesi sulla
struttura interna del sistema
– Generalmente sono in numero limitato
– Sono suggerite dai nostri sensi
– Sono misurabili direttamente
Per es: sistema costituito dal gas contenuto
nel cilindro del motore dell’automobile
– Il volume occupato
– La pressione esercitata sulle pareti
– La temperatura
– La composizione
•
Punto di vista microscopico
– parte da un’ipotesi della struttura
della materia (gas costituito da
molecole). – Si descrive il comportamento di
ciascuna molecola (posizione,
velocità, energia cinetica, quantità
di moto, etc) – È necessario un numero elevato di
grandezze per descrivere il
comportamento del sistema
– Che non hanno niente a che vedere
con le nostre percezioni sensoriali
– Che sono difficili da misurare
direttamente
I due punti di vista sono complementari
– Le grandezze macroscopiche sono la media di quelle microscopiche
– Il punto di vista macroscopico è più stabile
I sistemi termodinamici
•
•
La termodinamica si applica a tutto: qualunque oggetto presente in natura può
costituire un sistema termodinamico.
Le coordinate termodinamiche utili per descrivere lo stato del sistema, dipendono
dal particolare sistema studiato:
– Per una sostanza pura (sostanza costituita da un’unica specie molecolare)
• Pressione, volume, temperatura
– Per un filo sottoposto a tensione
• Sforzo, allungamento e temperatura
– Per una cella elettrolitica
• Forza elettromotrice, pressione e temperatura
•
In molti casi sono sufficienti due sole coordinate termodinamiche per descrivere
lo stato di un sistema
– Per una sostanza pura (sostanza costituita da un’unica specie molecolare)
• Pressione e volume,oppure temperatura e volume, oppure temperatura e pressione
– Nel seguito noi faremo riferimento a sistemi termodinamici descrivibili con due sole
coordinate termodinamiche, X e Y.
•
Come già detto la temperatura gioca un ruolo fondamentale in termodinamica
– Dobbiamo darne una definizione operativa
L’equilibrio termico
•
•
•
•
Un sistema termodinamico si trova in uno stato di equilibrio
caratterizzato da ben determinati valori delle coordinate X e Y, se i
valori delle coordinate X e Y non cambiano fino a che non cambiano
le condizioni esterne.
Quando le condizioni esterne cambiano, anche lo stato del sistema,
e quindi le sue coordinate termodinamiche, possono cambiare
Il comportamento di un sistema termodinamico dipende dal tipo
di interazione che può avere con l’ambiente esterno
Le interazioni dipendono dal tipo di
sistema dall’ambiente esterno :
pareti che separano il
– Adiabatiche
X,Y
X,Y
sistema
• Le coordinate termodinamiche del sistema variano, comunque
dopo un tempo più o meno lungo, il sistema raggiunge un nuovo
stato caratterizzato da nuove coordinate termodinamiche che
rimangono costanti fino a che non cambino nuovamente le
condizioni esterne
• Si è raggiunto uno stato di equilibrio termico
ambiente
Stato iniziale
• Le coordinate termodinamiche del sistema non cambiano al
cambiare delle condizioni esterne
– Conduttrici
X', Y'
Xi ,Yi
X'i ,Y'i
sistema
ambiente
Stato finale
Xf,Yf
X'f,Y'f
Il principio zero della termodinamica
•
due sistemi in equilibrio termico con un terzo sistema, sono in equilibrio
termico tra loro.
•
Questo principio è la base della misura della
temperatura
–
se il sistema A è in equilibrio termico con un
determinato stato del sistema C (termometro)
– se il sistema B è in equilibrio termico con lo stesso
stato del sistema C (termometro) – Allora i due corpi A e B hanno la stessa temperatura.
Definizione operativa della temperatura
L’uomo , attraverso il tatto, ha una percezione sensoriale della temperatura
– Riesce a distinguere un corpo più caldo da uno più freddo
– Comunque la determinazione di un numero (il risultato della misura) solo sulla base
della percezione sensoriale è molto soggettiva
• Ci sono situazioni di palese contraddizione:
–
se, in una giornata molto fredda, si tocca un oggetto di legno ed uno di ferro, tutte due alla stessa
temperatura, quello di ferro ci darà l’impressione di esser più freddo
– Se si tocca lo stesso oggetto con le due mani, che abbiamo tenuto per qualche minuto una in una
bacinella di acqua calda e l’altra in una di acqua fredda, otterremo dalle due mani della sensazioni
contraddittorie.
– Bisogna usare uno strumento di misura
– Si fa riferimento a sistemi termodinamici per i quali, mantenendo fissa una delle due
coordinate termodinamiche, l’altra varia con la temperatura
• Per esempio è noto che a pressione costante, i corpi si dilatano
– Un termometro classico è costituito da una certa quantità di mercurio che si espande all’interno di un
capillare, la lunghezza del mercurio nel capillare è legata alla temperatura
• La pressione di una certa quantità di gas contenuta in un volume costante dipende dalla
temperatura
– Termometro a gas a volume costante
• La forza elettromotrice di una cella elettrolitica che lavora a pressione costante dipende dalla
temperatura.
Taratura di un termometro
Una volta selezionato il tipo di termometro da usare
– Per esempio la lunghezza del mercurio in un capillare
Dobbiamo procedere alla taratura del termometro, – trovare la legge di corrispondenza tra il valore della grandezza
termometrica utilizzata •
la lunghezza del mercurio nel capillare
– con il valore della temperatura da misurare
•
Per la taratura si fa ricorso a cosiddetti “punti fissi”
– Per punto fisso si intende un particolare sistema termodinamico in cui la temperatura del sistema
resta invariata fin tanto che perdurano determinate condizioni
•
•
La temperatura di fusione del ghiaccio alla pressione atmosferica resta costante fintanto che il sistema risulta
composto da acqua allo stato liquido o acqua allo stato solido (ghiaccio) (tratto VERDE )
La temperatura di ebollizione dell’acqua alla pressione atmosferica resta costante fintanto che il sistema
termodinamico risulta composto di acqua nella fase liquida ed vapore acqueo (tratto ROSSO)
Taratura di un termometro
•
Per molto tempo si è usata una definizione di temperatura basata sul punto di
fusione e sul punto di ebollizione dell’acqua
–
–
–
–
Al punto di fusione dell’acqua è stato assegnato arbitrariamente il valore 0°C
Al punto di ebollizione il valore 100° C
L’intervallo di temperatura è stato suddiviso in 100 parti (gradi centigradi)
Se chiamiamo • LF la lunghezza del mercurio nel capillare quando è in equilibrio termico con il punto di fusione
dell’acqua
• Le la lunghezza del mercurio nel capillare quando è in equilibrio termico con il punto di
ebollizione dell’acqua
• L la lunghezza del mercurio nel capillare quando è in equilibrio termico con il corpo di cui si
vuol misurare la temperatura
L − Lf
T=
100 °C
Le − Lf
Le scale Celsius e Fahrenheit
•
•
•
•
•
•
•
Della scala Celsius, o centigrada,
abbiamo già parlato
L’unità di misura della scala
Celsius, 1°C, è uguale al
campione della scala Kelvin, 1 K.
1°C=1K
Esiste solo un offset tra le due
scale
Infatti alla temperatura di 0°C
corrisponde una temperatura di
273.15 K.
La relazione tra le due
temperature è la seguente:
tc temperatura in gradi Celsius
T temperatura in K (kelvin)
•
•
La scala Fahrenheit fa coincidere
al punto di fusione dell’acqua la
temperatura tf=32°F, e a quello di
ebollizione la temperatura di
tf=212°F
La relazione tra temperatura
Fahrenheit e centigrada è data da
t F = 32 +
212 − 32
9
t C 032 + t C
100
5
9
t F = 32 + t C
5
tC =
5
(t F − 32 )
9
La dilatazione termica
Abbiamo già accennato al fatto che i corpi si
dilatano con la temperatura
Ora che abbiamo una definizione più precisa della
temperatura, possiamo studiare con una
maggiore accuratezza il fenomeno
Cominciamo dai corpi solidi
In particolare corpi unidimensionali (un filo, una
sbarra, etc)
1 dl
α=
l dT
Coefficiente di dilatazione lineare
• Dipende dalla temperatura
• Per intervalli limitati di
temperatura può essere
considerato costante
La dilatazione superficiale e di volume
•
Se si ha a che fare con una lastra rettangolare, di un materiale isotropo,
entrambe le dimensioni si dilateranno con la stessa legge:
(
)
l ' = l (1+ α ΔT)
A' = l' l ' = l (1 + α ΔT )l (1 + α ΔT )=
l l (1+ 2α ΔT + α ΔT )
l ' 1 = l 1 1 + α ΔT
2
2
1
2
1
2
2
l1
2
1 2
Trascurando α2ΔT2 rispetto a 2αΔT à
(
A' = A 1 + 2α ΔT
l2
)
Il coefficiente di dilatazione superficiale è due volte quello lineare
In maniera analoga si può vedere che il coefficiente di dilatazione
cubica è tre volte quella lineare
(
V' = V 1+ 3α ΔT
)
l3
l1
l2
La dilatazione di volume dei liquidi
Nel caso dei liquidi non è possibile parlare di
dilatazione lineare o superficiale
Si parla solo di dilatazione di volume, o cubica:
V' = V(1+ βΔT)
materiale
β (K-1)
acqua
1.8 10-4
Alcol etilico 10.4 10-4
benzina
9.6 10-4
cloroformio 14.0 10-4
glicerina
5.3 10-4
mercurio
1.8 10-4
I valori del coefficiente di dilatazione di volume per i liquidi sono più grandi, circa
un fattore 10, dei corrispondenti valori per i solidi (legame molecolare più debole)
L'acqua ha un comportamento diverso dagli altri liquidi. – Aumentando la temperatura al di sopra dei 4 °C l'acqua si dilata anche se non
in maniera lineare. – Ma anche diminuendo la temperatura al di sotto dei 4 °C l'acqua continua a
dilatarsi (il ghiaccio ha una densità più bassa dell’acqua) .
N.B. Quando i fiumi si raffreddano, l’acqua più fredda, o il ghiaccio, sale in
superficie, l’acqua sul fondo del fiume non scende mai al di sotto dei 4° C (solo
così i pesci possono sopravvivere).
L'acqua ha dunque una densità massima alla temperatura di 4 °C: in queste
condizioni essa differisce per meno di 1 parte su 10000 da 1 gr/cm3. A tutte le altre temperature, la densità dell'acqua è minore di questo valore.
Esercizio: Un’asta di acciaio ha un diametro di 3.0 cm alla temperature di 25°C. Un
anello di ottone ha un diametro interno di 2.992 cm alla temperatura di 25°C. A
quale temperatura comune l’asta si infilerà nell’anello.
Dalla tabella dei coefficienti di dilatazione lineare ricaviamo
αottone=19x10-6 °C-1
αacciaio=11x10-6 °C-1 d asta = d asta _ 25°C (1 + αacciaoΔT )
d anello = d anello_ 25°C (1+ α otton eΔT)
Imponiamo l’uguaglianza tra i due diametri e ricaviamo la variazione di
temperatura ΔT comune
d asta _ 25°C (1 + αacciaoΔT) = d anello _ 25°C (1 + αotton eΔT )
d asta _25°C − danello_25°C = danello_25°Cα ottoneΔT − dasta _ 25°CαacciaoΔT =
ΔT =
dasta _ 25°C − d anello_ 25°C
=
d anello_ 25°C αottone − dasta _ 25°C αacciao
3.000cm − 2.992cm
0.008 × 106
=
=
= 335.4°C
−6
−1
−6
−1
2.992cm
×
19
×
10
°C
−
3.000
×
11
×
10
°C
23.848
1 44 2 4 43
14 2 43
56.848
33.000
ΔT = T − 25°C = 335.4°C ⇒ T = 335.4°C + 25°C = 360°C
Esercizio 1: Si riempie fino all’orlo un contenitore di pyrex di capacità 1litro con
acqua a 10°C. Si scalda quindi il recipiente, aumentando la temperatura
dell’acqua fino a 30°C. Quanta acqua fuoriesce dal contenitore? βacqua=0.207 ⋅
10-3K-1 et αpirex=3.25 ⋅ 10-6K-1
R= 4 ml.
Esercizio 2: Un tratto rettilineo di un oleodotto lungo 220 m si trova alla temperatura
di -50°C prima di essere riempito dal petrolio a temperatura massima 64°C.
L’oleodotto è avvolto da una guaina isolante, in modo che la tubatura ed il
petrolio abbiano la medesima temperatura.
a) Determinare di quanto si dilata la tubatura quando è riempita di petrolio;
b) Se lo stesso effetto si verificasse per tutto l’oleodotto che è lungo 676Km, quale
sarebbe la sua variazione complessiva di lunghezza ?
R. 28cm et 860m
Esercizio 3: La base di acciaio di un ponte sospeso è lunga 200m a 20°C. Se le
temperature estreme alle quali è esposto sono -30°C e +40°C, che intervallo
devono compensare i giunti del ponte ? αacciaio=12 ⋅10-6K-1
R. 4.8cm +12cm= 16.8cm
Esercizio 4: A Parigi la massima e la minima temperatura rilevate tra la notte ed il
giorno sono state le seguenti: -28°C et 22°C. Sapendo che, alla temperatura
minima, essa è alta 301m e che per l’acciaio αacciaio=12 ⋅ 10-6K-1 determinare la
sua altezza.
R. +18cm
Equilibrio Termodinamico
Un sistema termodinamico si dice isolato se non ha interazioni con l’ambiente
Qualunque sia lo stato di partenza del sistema, anche se – la pressione all’interno del sistema è differente da punto a punto ed è differente da quella
esterna – La temperatura del sistema è differente da punto a punto ed è differente da quella esterna
– Il sistema, a causa della differenza di pressione, è soggetto a moti turbolenti, con
accelerazioni, etc
– Tra le varie componenti del sistema possono avvenire reazioni chimiche
aspettando un tempo sufficientemente lungo si
osserva che il sistema si porta in
uno stato stazionario (si esauriscono i moti)
– in cui sono cessate tutte le reazioni chimiche
– in cui la pressione risulta essere la stessa in tutti i punti del sistema, e se il sistema non è
isolato meccanicamente dall’ambiente esterno deve essere la stessa di quella esterna
– e in cui la temperatura risulta essere la stessa in tutti i punti del sistema, e se il sistema
interagisce con l’ambiente esterno attraverso pareti conduttrici, è la stessa di quella
esterna
Il persistere contemporaneamente dei tre equilibri: meccanico, termico, chimico, à realizza l’equilibrio termodinamico.
Equilibrio Termodinamico
Si dirà che il sistema si trova in equilibrio termodinamico, se esso si trova
contemporaneamente in:
– equilibrio meccanico, quando non esistono forze o momenti non equilibrati né all'interno
del sistema, né tra il sistema e l'ambiente circostante. • la pressione deve essere la stessa in tutte le parti del sistema e, se il contenitore non è rigido, essa
è la stessa dell’ambiente circostante.
– equilibrio termico, quando tutte le parti del sistema hanno la stessa temperatura, e se le
pareti che circondano il sistema sono conduttrici, questa coincide con quella dell'ambiente
circostante.
– equilibrio chimico, quando non avvengono processi che tendono a modificare la
composizione del sistema, come reazioni chimiche, né spostamenti di materia da una parte
all'altra del sistema, come accade per esempio quando una sostanza entra in soluzione o
quando una sostanza cambia fase, per esempio da liquido a vapore. (Con l'espressione
reazione chimica si intendono sia le reazioni chimiche vere e proprie che il trasporto di
materia e i cambiamenti di fase.)
Gli stati di equilibrio termodinamico sono estremamente importanti
Si riesce a descrivere solo gli stati di equilibrio termodinamico
In uno stato di non equilibrio termodinamico la pressione può variare da punto a punto. Quale valore possiamo assegnare all’intero sistema?
Non è possibile descrivere gli stati che non siano di equilibrio!
Il piano PV o piano di Clapeyron
•
•
•
•
Se il sistema è in equilibrio termodinamico, allora sono definite le coordinate
termodinamiche relative a quello stato.
Molti sistemi termodinamici hanno bisogno di solo due coordinate
termodinamiche per individuare un particolare stato
Tipico è l’esempio delle sostanze pure per le quali sono sufficienti le coordinate
pressione e volume per individuare il particolare stato
Lo stato di equilibrio può essere rappresentato in un diagramma (piano PV o
piano di Clapeyron) così fatto:
P
Coordinate
Attenzione: solo gli stati di
equilibrio termodinamico
Possono essere rappresentati
nel piano PV
Pi
i
Vi
termodinamiche
(Vi,Pi)
V
L’equazione di stato
•
Sostanze pure
– Solo due coordinate termodinamiche sono sufficienti per identificare gli stati di
equilibrio termodinamico
• Per esempio pressione e volume (le due coordinate di tipo meccanico)
– Cosa succede della terza coordinata termodinamica, la temperatura?
• Si vede che una volta determinato lo stato, ossia una volta scelto il valore del volume e della
pressione, la temperatura è univocamente determinata dalla scelta delle altre due coordinate.
• Esiste una relazione che lega tra loro le coordinate termodinamiche!!
•
•
f(V,P,T)=0
Questa funzione implicita rappresenta l’equazione di stato.
Generalmente l’equazione di stato non è nota. – Essa va determinata sperimentalmente o dedotta per via teorica
– Per noi è importante sapere che tutti i sistemi termodinamici hanno una equazione di
stato che lega le coordinate termodinamiche di tipo meccanico (P e V) alla temperatura.
– L’equazione di stato più nota è quella del gas perfetto:
PV=nRT
Esempio
• Un gas ha volume pari a 2 litri, temperatura 30°C e
pressione 1 atm. Quando il gas viene riscaldato a 60
°C e compresso fino ad un volume di 1,5litri, quanto
misurerà la pressione ?
[P=1,47atm]
Le trasformazioni
Consideriamo un sistema termodinamico in equilibrio
Per esempio una certa quantità di gas contenuto in un cilindro dotato di
pistone mobile
Supponiamo ora di alterare improvvisamente uno degli equilibri
Quello meccanico
Il pistone sotto l’azione della pressione interna non più bilanciata da quella
esterna si metterà in moto
La presenza di attriti tra pistone e cilindro può far variare la temperatura
localmente
L’aumento della temperatura può innescare reazioni chimiche
L’aver alterato uno degli equilibri, porta il sistema ad evolvere attraverso stati di non equilibrio
(la pressione è diversa da punto a punto e sicuramente diversa da quella esterna, lo
stesso vale per la temperatura)
verso un nuovo stato di equilibrio
Si è verificato un cambiamento di stato
Il sistema ha subito una trasformazione
Pgas = Pest +
Mg
A
Rappresentazione di una trasformazione nel
piano PV
In una trasformazione che procede per stati di non equilibrio termodinamico
Siamo in grado di conoscere coordinate termodinamiche solo nello stato di
partenza (iniziale) e nello stato di arrivo (finale)
Solo questi due stati possono essere rappresentati nel diagramma PV
P
la trasformazione non può essere
rappresentata nel diagramma PV.
Negli stati intermedi non è nota la pressione.
Pi
i
f
Pf
Vi
Vf
V
Le trasformazioni quasi statiche
•
Pgas = Pest +
Una trasformazione come quella descritta nella trasparenza precedente
non è descrivibile in termodinamica
– Non passa per stati di equilibrio termodinamico!!!
•
Dobbiamo costruire delle trasformazioni ideali nelle quali il sistema passa
attraverso stati di equilibrio termodinamico (o comunque stati vicinissimi
ad uno stato di equilibrio termodinamico)
– Solo così è possibile descrivere la trasformazione
– Ed eventualmente fare dei conti
Per esempio, se suddividiamo la massa M poggiata sul
pistone in tanti piccoli pesetti,
–
e togliamo un pesetto alla volta, ci saremo allontanati poco
dallo stato di equilibrio iniziale
– aspettiamo ora il tempo necessario perché l’equilibrio
comunque si ripristini, e poi togliamo un secondo pesetto.
– Così facendo potremo portare il sistema dallo stesso stato
iniziale allo stesso stato finale della trasformazione
precedente
– Ma in questo caso durante tutta la trasformazione siamo
passati attraverso stati di equilibrio o stati molto prossimi a
stati di equilibrio, e quindi confondibili con essi.
Pi Vi
Pi -ΔP
V i +ΔV
Mg
A
Trasformazioni reversibili
Trasformazione quasistatica
Definizione: È una trasformazione in cui il sistema passa per stati di equilibrio
•
Pi Vi
termodinamico o stati così prossimi ad uno di equilibrio termodinamico da poter
essere confusi con stati di equilibrio.
Una trasformazione quasi statica è una trasformazione ideale
– Richiede un tempo molto grande di esecuzione
Se non sono presenti effetti dissipativi,
– Lavoro effettuato da forze non conservative (forze di attrito dinamico)
– Passaggi di corrente all’interno di resistori
Allora la trasformazione può essere percorsa all’indietro.
– Consideriamo la trasformazione quasi statica che abbiamo descritto
– Supponiamo di aver già tolto un certo numero di pesetti
– Anziché continuare a togliere i pesetti dal pistone, possiamo rimetterli ad
uno ad uno sul pistone.
– Quando li avremo rimessi tutti avremo riportato il sistema nello stato da cui
eravamo partiti
– Abbiamo cioè percorso la trasformazione all’indietro.
La trasformazione si dirà reversibile.
– Una trasformazione per essere reversibile deve essere quasistatica e non
devono essere presenti effetti dissipativi.
Pi -ΔP
V i +ΔV
Rappresentazione di una trasformazione
reversibile nel piano PV
•
•
•
•
In una trasformazione reversibile tutti gli stati intermedi sono di equilibrio
termodinamico
Quindi siamo in grado di conoscere le coordinate termodinamiche in tutti gli stati
intermedi
Possiamo rappresentare una trasformazione reversibile nel piano PV, mediante
una linea continua che connette lo stato iniziale con quello finale
Una trasformazione reversibile può essere suddivisa in tratti infinitesimi
P
Pi
i
Pf
P
f
V
Vf
Vi
V
Espansione isoterma reversibile
•
•
•
•
•
•
Realizziamo una espansione isoterma in maniera reversibile
di un certa quantità di gas contenuta in un cilindro chiusa da
un pistone mobile
Togliendo un pesetto, la pressione esterna si abbassa, il gas si espande, il suo volume diventa più grande,
durante l’espansione il gas si raffredda poco, assorbe pertanto un po’ di calore dal termostato per tornare
alla temperatura costante T
In tutto questo processo, se il pesetto rimosso è piccolo, il gas
si trova o in uno stato di equilibrio o in uno stato molto vicino
ad uno di equilibrio che può approssimato con uno stato di
equilibrio
Se non ci sono attriti la trasformazione può essere percorsa
anche al contrario
– Anziché togliere i pesetti, si rimettono ad uno ad uno sul pistone
Pi Vi
Τ
Pi -ΔP
V i +ΔV
Τ
P
i
Stati di equilibrio
termodinamico
f
Stati che differiscono da uno stato
equilibrio termodinamico per un
infinitesimo
V
Trasformazioni causate da una differenza di temperatura
Abbiamo già accennato al fatto che alcune trasformazioni sono
causate dalla mancanza di equilibrio termico
Se la temperatura dell’ambiente esterno è diversa da quella
del sistema :
– Il sistema e l’ambiente esterno interagiscono fino a
raggiungere un valore comune di temperatura
(generalmente quella dell’ambiente esterno)
– Possiamo immaginare che l’interazione è avvenuta
attraverso lo scambio di qualcosa che chiameremo
calore, senza meglio precisare cosa sia (per il
momento).
– Vedremo in seguito che il calore altro non è che
l’energia scambiata tra sistema e ambiente circostante
a causa della differenza di temperatura La calorimetria
•
Prima che attraverso il lavoro di Joule si riuscisse a stabilire l’equivalenza tra il
calore e il lavoro meccanico,
– E quindi identificare il calore come una forma di energia
•
•
Molto pragmaticamente, i fisici avevano dato una definizione operativa del calore.
Questa definizione parte dalla osservazione che molti sistemi termodinamici
variano la loro temperatura quando acquistano o cedono del calore.
•
Se un sistema termodinamico a cui viene ceduta una quantità di calore Q
subisce una variazione di temperatura ΔT
Q
C=
Si definisce capacità termica il rapporto
ΔT
•
•
Naturalmente questa è la Capacità media nell’intervallo di temperatura ΔT.
La Capacità termica è una funzione della temperatura.
Se si vuole determinare la capacità termica ad una particolare temperatura
bisogna effettuare il passaggio al limite
C = lim ΔT →0
•
Q
dQ
=
ΔT dT
Per tutti gli effetti pratici la capacità termica può essere considerata costante per
variazioni di temperatura limitate intorno alla temperatura ambiente.
Il calore specifico
Il calore specifico è la capacità termica riferita all’unità di massa
Consideriamo il sistema termodinamico di massa m
A cui viene somministrato il calore Q
Subisce una variazione di temperatura ΔT
Il calore specifico è anche uguale alla capacità termica diviso la massa.
Questa definizione è l’equazione fondamentale per definire il campione di calore: la caloria
Definizione della
caloria
• Si sceglie una particolare sostanza: l’acqua e le si assegna arbitrariamente calore specifico 1
• Si prende l’unità di massa di questa sostanza: 1g
• Si prende una variazione unitaria di temperatura
La caloria è dunque la quantità di calore che riesce a far aumentare la temperatura di un
grammo di acqua da 14.5 °C a 15.5 °C alla pressione atmosferica.
– L’acqua dunque ha un calore specifico di 1 cal/(g°C) alla pressione atmosferica e a 15°C.
Analogamente definiremo CALORE SPECIFICO MOLARE come la capacità
termica riferita alla numero di moli della sostanza. Il calore somministrato al corpo, invertendo la definizione di calore specifico
è dato da:
Tabella dei calori specifici
Anche i calori specifici come la capacità termica dipendono dalla temperatura
Comunque per piccole variazione della temperatura nell’intorno della temperatura ambiente
possono essere considerati costanti.
• Il calore specifico dell'acqua
diminuisce tra zero e 35°C poi
cresce nuovamente; [vale 1.007 cal/g°C sia a 0°C che a
100 °C, mentre vale 0.998 cal/g°C
intorno a 35 °C. ]
• varia poco tra 0°C e 100°C, si può
considerare costante.
I calori specifici, dipendono anche
dal tipo di trasformazione con cui
viene ceduto il calore.
• Per i solidi ed i liquidi è facile
effettuare
trasformazioni
a
pressione costante (pressione
atmosferica).
• Per i gas vengono forniti due
valori (diversi), a pressione e a
volume costante.
CS = F(T, trasformazione, etc.)
1 Q
C molare =
n ΔT
La misura del calore -il calorimetro
•
•
•
Per la misura del calore si può usare un strumento
come quello illustrato in figura
È costituito da una certa quantità di liquido, per es.
acqua, in un recipiente il tutto circondato da pareti
adiabatiche, per evitare scambi di calore con
l’esterno.
Completano lo strumento Termometro
Agitatore
– Un agitatore per far si che la temperatura diventi
uniforme nel più breve lasso di tempo
– E un termometro che misura la temperatura del
liquido.
•
•
•
è necessario conoscere la capacità termica Ctotale del
liquido, recipiente, agitatore e termometro
Si misura la temperatura iniziale, Ti, e finale Tf, ossia
dopo il trasferimento di calore Il calore scambiato sarà dato da:
(
Q = C totale T f − Ti
)
Esercizio: Calcolate il calore specifico di un metallo dai seguenti dati. Un
contenitore fatto di questo metallo ha una massa di 3.6kg e contiene 14 litri
di acqua. Un pezzo di metallo m=1.8Kg inizialmente alla temperatura di
180°C viene immerso nell’acqua.
Il contenitore e l’acqua inizialmente hanno una temperatura di 16 °C e la
temperatura finale di tutto il sistema è 18°C.
Dalla tabella dei calori specifici ricaviamo che quello dell’acqua vale
: cacqua=4190 J/ kgK
Osserviamo che il calore ceduto dal pezzo di metallo è stato tutto acquisito
dall’acqua e dal contenitore.
Il calore ceduto dal pezzo di metallo vale
c
metallo
Q = cmΔT
Il calore acquisito dall’acqua e dal contenitore vale:
Qa = cacquamacquaΔTacqua + cmcontenitoreΔTacqua
cacquamacquaΔTacqua + cmcontenitoreΔTacqua = −mcΔTmetallo
c=−
cacqua macqua ΔTacqua
mΔTmetallo + mcontenitore ΔTacqua
4190 ×14 × 2
117320
J
=−
=
= 412
1.8 × (− 162) + 3.6 × 2 284.4
kgK
Il serbatoio di calore o termostato
Con questo nome indicheremo un sistema termodinamico tale che può
assorbire o cedere quantità anche rilevanti di calore senza che la sua
temperatura vari apprezzabilmente.
Dalla definizione di capacità termica appare che un tale sistema deve avere
una capacità termica molto elevata o equivalentemente una massa molto
grande
Nota:
Serbatoi di calore naturali sono gli oceani e l’atmosfera
Trasformazioni con scambio di calore
Trasformazioni con trasferimento di calore ma
senza aumento di temperatura
Cambiamenti di fase
Somministrando calore al sistema
La temperatura non varia
Varia invece la quantità di sostanza che ha cambiato fase,
Q=LFΔm
fusione
Q=LvΔm
evaporazione
Esercizio: Un thermos isolato contiene 130 g di caffè caldo, alla temperatura di 80° C.
Per raffreddare il caffè aggiungete all’interno del thermos un cubetto di ghiaccio di massa 12g
tolto da una cella frigorifera alla temperatura di -10°C. Di quanti gradi si sarà raffreddato il caffè
dopo che il ghiaccio si è fuso e si sarà raggiunta la condizione di equilibrio finale? Trattate il caffè
come se fosse acqua pura e trascurate gli scambi termici con l’ambiente circostante.
Dalla tabella dei calori specifici e da quello dei calori latenti ricaviamo:
cacqua=4190 J/ kgK,
cghiaccio=2220J/kgK,
Lf=333kJ/kg
Il ghiaccio subirà le seguenti trasformazioni
– Riscaldamento da -10°C a 0°C
Q1=mghiacciocghiaccio (Tf=0°C-Ticghiaccio)=266.4J
– Fusione a 0°C
Q2=mghiaccioLf=3996J
– Riscaldamento da 0°C alla temperatura finale Q3=mghiacciocacqua (Tf-T0°)
Il caffè, invece, subirà la seguente trasformazione
– Raffreddamento da 80°C alla temperatura finale Q4=mcaffècacqua (Tf-Ticaffè) (<0)
Problemi per casa.
1) I polmoni di una persona adulta possono contenere 6,0 litri d’aria alla temperatura del
corpo (t=37°C) e alla pressione atmosferica (P=1,013 10+5 Pa). Dato che l’aria contiene il 21%
di ossigeno, trova il numero di molecole di ossigeno contenute nei polmoni. 2) L’aula che occupiamo misura una base di 8mx12m ed altezza 7m. Se la temperatura è di
22°C e la pressione è 1atm, determinare il numero di moli di gas che si trovano all’interno
dell’aula.
Quanti respiri può fare uno studente ? Se mediamente fa 10 respiri al minuto, per quanto
tempo sopravvivrà ?
3) Supponi che la pressione di una palla da basket sia di 171 kPa, ad una temperatura di 20
°C, e che il suo diametro sia di 30,0 cm.
1. Quante moli di aria contiene una palla da basket gonfia? 2. Qual è la pressione dell’aria contenuta, espressa in atm ?
NOTA: Una mole di una sostanza è quella che contiene 6.022 x 1023 particelle di quella
sostanza. Le particelle possono essere – atomi, molecole, mele o anche persone. Se avessi il
numero di Avogadro di popcorn, potresti sotterrare gli Stati Uniti sotto uno strato di 15Km di
popcorn. Il numero 6,022 x 10+23 è detto numero di Avogadro: NA= 6.022 x 1023