Diapositiva 1 - Docenti.unina

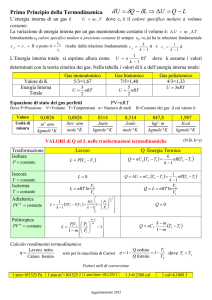
Esercizio 1. La potenza necessaria per portare in 2 ore 60 litri di acqua da 20 °C a 80
°C vale circa:
a) 1800 kcal
b) 7.2 kWh
c) 2 kW
d) 2 J/s
La potenza è data da:
L
P
t
J
  W
s
Il calore necessario per innalzare la temperatura del volume
d’acqua da 20 °C a 80 °C è:
Q = m c T
Dall’equivalente meccanico della caloria:
L
J
Q
L=QJ
Quindi la potenza richiesta:
cmΔTJ (1kcal/kg C)  (60kg)  (60C)  (4186J/kca l)
P


t
2  (3600s)
 2kW
Esercizio 2. La temperatura di una massa di 1 grammo di ferro passa da 18 °C a 20
°C, alla pressione atmosferica. Calcolare la variazione di energia interna della massa
di ferro. (calore specifico del ferro c = 448 J/kg K, coefficiente di dilatazione termica
del ferro  = 1.1 10-6 K-1, densità del ferro 7.8 103 kg/m3).
a) 8.9 10-1 J
b) 1.1 MJ
c) 9.8 10-4 J
d) 0.6 kJ
e) 2.3 J
Applichiamo il primo principio della termodinamica:
U = Q - L
La quantità di calore scambiata dalla massa di ferro è:
Per calcolare il lavoro L bisogna considerare la dilatazione termica della massa:
Il lavoro L (trasformazione isobara):
Il lavoro è trascurabile rispetto al calore Q, quindi possiamo scrivere:
U = Q – L  8.9 10-1 J
Esercizio n. 3 In una trasformazione isobara di un gas perfetto la variazione di
energia interna è ΔE = -240 kcal mentre la variazione di entalpia è ΔH = -260
kcal. Quale delle seguenti affermazioni è corretta?
a) la temperatura del sistema non varia
b) il sistema si espande
c) il volume del sistema diminuisce
d) l’entropia aumenta
e) nessuna delle precedenti
I° principio della termodinamica per trasformazioni isobare:
U = Q – L= Q – pV
Sappiamo che l’entalpia è data da:
H = U +pV
Per una trasformazione isobara la variazione di entalpia è:
H = U + (pV) = U + pV
Sostituendo il I° principio della termodinamica abbiamo:
H = Q – pV + pV = Q <0
L’entropia non può aumentare
La variazione di energia interna è:
U = H – pV
Abbiamo quindi che la variazione di volume è:
ΔV 
ΔH  ΔU (260kcal  240kcal)

0
p
p
Quindi
V <0
Per un gas perfetto
Il volume del sistema diminuisce
U  T quindi la temperatura del sistema
diminuisce (dal testo U <0)
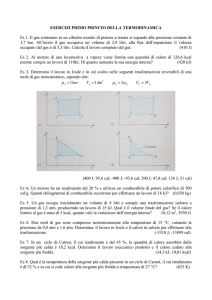
Esercizio n. 4 Una macchina termica opera utilizzando un gas perfetto monoatomico
secondo il ciclo mostrato in figura con p(B) = 3 atm, V(A) =0.1 l, V(B) = 1 l e p(C)
= 1 atm. Il lavoro fatto nell’intero ciclo vale:
a) 91 J
b) 0 J
c) 1000 kcal
d) 120 MJ
p
A
B
C
Il lavoro fatto nell’intero ciclo è dato dall’area delimitata dal ciclo:
LABC   pdV
Quindi:
LABC 
V(B)  V(A)  p(B)  P(C) 
2
1  0.1 ) 10 3 m 3  2 1.01105 Pa

 0.9110 2 m 3 Pa  91J
2

 

V
Esercizio n. 5 Una centrale elettrica opera al 80% del suo rendimento teorico di
Carnot tra le temperature 300 °C e 700 °C. Se la centrale eroga 1.3 GW di potenza,
quanto calore disperde in un’ora?
a) 2.6 109 J/h
b) 1010 J/h
c) 9.5 1012 J/h
d) 2 kcal/h
Il rendimento ideale di una macchina di Carnot è dato da:
η  1
Il rendimento reale della centrale elettrica vale:
ηR  0.80  0.41  0.33
Inoltre sappiamo che il rendimento si può esprimere anche:
η
L
L

Q A L  QC
ηL  ηQ C  L
T2
573
 1
 0.41
T1
973
η
L
QA
L(1  η)
QC 
η
(1.3 109 J/s)  (1  0.33)
QC 
 2.64 109 J/s  9.5 1012 J/h
0.33
Esercizio n. 6 Due moli di elio gassoso, inizialmente alla temperatura di 300 K e alla pressione
di 0.400 atm, subiscono una compressione isoterma fino ad una pressione di 1.20 atm.
Assumendo che il gas si comporti come un gas perfetto, determinare il volume finale del gas, il
lavoro compiuto sul gas, l’energia trasferita tramite calore.
a) 0.0290 m3, -3.33kJ, 3.33kJ
b) 44.5 dm3, 2.78 J, 3.44 J
c) 0.0410 m3, -5.48 kJ, -5.48 kJ
d) 5 l, 6.56 kJ, -6.56kJ
e) 0.029 mm3, 6.67J, 9.21 kJ
Dall’equazione di stato dei gas perfetti ricaviamo il volume iniziale:
Vi 
nRT (2 moli )(8.31 J / mol  K )(300 K )

 0.123 m3
5
pi
(0.400atm)(1.0110 Pa / atm)
Per una compressione isoterma
V f  Vi
Il lavoro compiuto dal gas è:
PiVi = PfVf:


Pi
 0.400 atm 
3
 0.123 m3 
  0.0410 m
Pf
 1.20 atm 
f
Vf
dV
 0.0410 
L  nRT 
 nRT ln
 (2  8.31J / mol  K )  (300 K )  ln 
  5.48 kJ
V
Vi
 0.123 
i
QL
Q  5.48 kJ
U  Q  L  0
Se l’ambiente compie sul sistema il lavoro L, il sistema, per mantenere costante
U, deve cedere una pari quantità di energia all’ambiente sotto forma di calore.
Esercizio n. 7 Una sorgente alla temperatura di 576 K trasferisce 1050 J di calore ad
una sorgente alla temperatura di 305 K attraverso una trasformazione irreversibile.
Calcolare la variazione di entropia del sistema.
a) 1.62 J/K
b) 2.98 J/K
c) 7.00 J/K
d) 5.78 J/K
e) 9.10 J/K
La variazione di entropia della sorgente calda è:
S c  
Q
1050 J

 1.82 J / K
Tc
576 K
Tc = 576 K
Q = 1050 J
La variazione di entropia della sorgente fredda è:
TF= 305 K
Q 1050 J
S F 

 3.44 J / K
TF
305K
Sommiamo i contributi per ottenere la variazione di entropia del sistema:
S sistema  Sc  S F  
Q
TC

Q
TF
 (1.82  3.44 ) J / K  1.62 J / K
Esercizio n. 8 Una massa di 100 g di piombo a 100 °C viene immersa in un calorimetro
contenente 200 g di acqua a 20 °C. Trovare la variazione di entropia del sistema tra lo stato
finale e lo stato iniziale (calore specifico del piombo cPb = 000345 cal/g°C e dell’acqua cH2O =
1 cal/g°C).
a) 1.2 cal/K
b) 0.11 cal/K
c) 9.0 cal/K
d) 0.45 cal/K
e) 6.9 cal/K
Una volta immersa la massa di piombo nel calorimetro, il sistema acqua-piombo
raggiunge la temperatura di equilibrio:
m Pb c Pb (TPb  TF )  c H 2O m H 2O (TF  TH 2O )
TF 
mPbcPbTPb  mH 2O cH 2OTH 2O
T2
cPb mPb  cH 2O mH 2O
 21 C
T
T2
dQ 2
dT
S


mc

mc
ln
Dalla definizione di entropia possiamo scrivere:
T T T T
T1
1
1
Dove c m dT è il calore assorbito o ceduto dal corpo di massa m durante la
variazione di temperatura dT.
La variazione di entropia del sistema acqua-piombo tra lo stato finale e quello
iniziale sarà quindi:
S  S Pb  S H 2O  mPbcPb ln
TF
T
294
294 

 mH 2O cH 2O ln F   3.45 ln
 200 ln
 cal / K  0.11 cal/K
TPb
TH 2O 
373
293 
Esercizio n. 9 Un recipiente cilindrico di sezione S = 1 dm2, chiuso superiormente da
un pistone di massa m = 10 kg e scorrevole verticalmente senza attrito, contiene n =
2 moli di un gas perfetto; le pareti del recipiente sono perfettamente trasparenti al
calore. L’ambiente esterno ha pressione P0 = 1 atm e temperatura T0 = 300 K. Si
aggiungono dei pallini di piombo sopra il pistone, fino a raddoppiarne la massa. Si
calcoli l’abbassamento h del pistone e il lavoro L subito dal gas, approssimando
come reversibile la trasformazione subita dal gas.
a) 3.8 10 -2m, -442 J
b) 38 10-4 m, -44.6 kJ
c) 3.8 102 mm, -30 J
d) 38 mm, 44.6 mJ
e) 3.8 mm, 4.6 kJ
Nello stato iniziale il pistone è in equilibrio sotto l’azione della sua forza peso e delle
forze dovute alla pressione esterna e alla pressione p1 del gas:
p1 
mg
 p0  1.1 atm
S
Nota la pressione iniziale a cui si trova il gas, possiamo determinare il volume
iniziale del gas:
nRT 2  ( 0.0821 atm  l/K  moli)  ( 300 K)
V1 

 44.8 l
p1
( 1.1 atm)
Dopo l’aggiunta dei pallini di piombo avremo nuovi valori di pressione e
volume:
p2  2
mg
 p0  1.2 atm
S
nRT 2  ( 0.0821 atm  l/K  moli)  ( 300 K)
V2 

 41.0 l
p2
( 1.2 atm)
Conoscendo la variazione di volume si può determinare l’abbassamento del
pistone:
V1  V2 (44.8 103  41.0 103 )m3
h 

 0.38 m
2
2
S
(110 )m
Poiché la trasformazione è isoterma e reversibile, il lavoro è dato da:
L
V2

V1
pdV  nRT
V2

V1
 41.0 10-3
dV
V2
 nRT ln
 2  (8.31J / K  moli )  (300 K ) ln 
 44.8 10-3
V
V1



  442 J

11
Esercizio n. 10 L’argon gassoso, che come tutti i gas nobili è monoatomico, viene
compresso lentamente in modo adiabatico in un cilindro isolato finché il suo volume
diventa la metà di quello iniziale Vi = 0.100 m3. Se all’inizio era a pressione
atmosferica (1 atm) ed alla temperatura di 27.0 °C, quanto varranno la pressione
finale e la temperatura finale?
a) 0.322 atm, 479 °C
b) 30 Pa, 30 K
c) 0.322 MPa, 478 K
d) 2 atm, 273 K
e) 322 mPa, 479 °C
Per le trasformazioni adiabatiche abbiamo:
Per gas monoatomici  = 1.67
Scriviamo l’equazione di stato dei gas perfetti per lo stato iniziale e finale:
Da cui: