IPSIA_2010(2)

Canali di comunicazione
Lezione tenuta presso l’Istituto
I.I.S.S. “Egidio Lanoce”
Maglie, 11 Febbraio 2010
Prof Antonio Cazzato
OBIETTIVI FORMATIVI
(Conoscenza e comprensione)
•
•
•
•
•
•
•
•
•
•
•
•
Saper definire una linea di trasmissione
Conoscere i tipi fondamentali di linee in cavo
Conseguenze della frequenza elevata: effetto Pelle
Saper definire le costanti primarie di una linea
Saper definire le costanti secondarie
Saper rappresentare il circuito elettrico equivalente di una linea
Sapere sotto quali condizioni una linea di lunghezza finita permette il
propagarsi di onde progressive
Saper definire le onde dirette e quelle riflesse
Saper comprendere il comportamento di una linea aperta o in corto circuito
se al suo ingresso si immette un segnale sinusoidale
Saper definire il coefficiente di riflessione
Conoscere l’origine e l’andamento di un’onda stazionaria (V ed I)
Comprendere l’andamento in ampiezza e fase dell’onda stazionaria
OBIETTIVI FORMATIVI
(Conoscenza e comprensione)
• Saper definire il ROS di una linea
• Saper calcolare i coefficienti di riflessione e ROS di una linea chiusa su un
carico resistivo noto
• Conoscere il legame tra il coefficiente di riflessione e ROS
• Comprendere il funzionamento di un adattatore a trasformatore l/4
• Comprendere cos’è uno “Stub” e come si realizza
• Comprendere come effettuare adattamento di impedenza con Stub e con
adattatori a trasformatore l/4
OBIETTIVI FORMATIVI
(Progettazione)
• Saper valutare, dalla lettura delle caratteristiche della linea, l’attenuazione in
funzione della lunghezza e della frequenza di lavoro
• Saper progettare un tronco di linea come circuito risonante ad una
determinata frequenza
• Saper dimensionare un adattatore di impedenza a l/4, note le frequenze di
lavoro, l’impedenza della linea e la resistenza di carico
Indice
•
INTRODUZIONE ALLE LINEE DI
TRASMISSIONE
•
EQUAZIONI GENERALI SULLA
PROPAGAZIONE
•
CLASSIFICAZIONE DEI MEZZI
TRASMISSIVI
•
CONDIZIONI DI PROPAGAZIONE
LUNGO LA LINEA
•
CARATTERISTICHE DEI CANALI
DI COMUNICAZIONE
•
COEFFICIENTE DI RIFLESSIONE
•
RAPPORTO SEGNALE RUMORE
•
SOGNIFICATO FISICO DEL
COEFFICIENTE DI RIFLESSIONE
•
L’ EFFETTO PELLE
•
•
LINEE DI TRASMISSIONE SU
SUPPORTI METALLICI
REGIME STAZIONARIO – L’ONDA
STAZIONARIA
•
ROS – RAPPORTO D’ONDA
STAZIONARIA SWR
•
IMPEDENZA DI INGRESSO
•
ADATTAMENTO CON TRONCO l/4
•
ADATTAMENTO CON STUB
•
DIVERSI TIPI DI LINEE
•
COSTANTI PRIMARIE
•
COSTANTI SECONDARIE
•
•
VELOCITA’ DI PROPAGAZIONE
LINEA NON DISTORCENTE
Introduzione alle Linee di Trasmissione
Un sistema di trasmissione è costituito da tre parti fondamentali:
•il lato trasmittente che rappresenta la sorgente dell’ informazione;
•il lato ricevente, che rappresenta la destinazione;
•il canale o mezzo trasmissivo che consente il trasferimento dell’ informazione.
GENERATORE
CARICO
•Dal mezzo trasmissivo dipendono maggiormente la qualità di trasmissione e le
prestazioni dell’ intero sistema.
•La scelta del mezzo trasmissivo deve essere legata al tipo di trasmissione e le
prestazioni dell’ intero sistema di trasmissione impiegato e deve consentire il
trasferimento di segnali che appartengono ad un certo campo di frequenze.
•I mezzi trasmissivi che vengono impiegati per trasmissioni di tipo analogico
devono consentire il trasporto dei segnali mantenendo inalterate le forme d’ onda
originarie istante per istante. Quelli impiegati invece per trasmissioni di tipo
numerico(bit) devono consentire il riconoscimento del valore del segnale
corrispondente in certi istanti di tempo per poterlo restituire in modo corretto.
•Un miglioramento della capacità del canale si può ottenere allargando la banda
passante o manipolando il rapporto segnale rumore (S/N).
I Mezzi Trasmissivi
Il mezzo trasmissivo non è altro che il mezzo lungo il quale si propagano i segnali da
una località all’altra cioè consentono il trasferimento dell’informazione. I mezzi
trasmissivi si dividono in due grandi gruppi in base al tipo di propagazione delle
onde.
1) Mezzi trasmissivi ad onde guidate (supporti fisici): in quanto esiste un
collegamento fisico tra il lato trasmittente ed il lato ricevente (tutti i mezzi in rame e
le fibre ottiche). Il loro difetto è relativo all’attenuazione che aumenta con la distanza.
2) Mezzi trasmissivi ad onde irradiate (ponti radio): in quanto non esiste un
collegamento fisico tra il lato trasmittente ed il lato ricevente, in quanto
l’informazione viaggia sotto forma di onde elettromagnetiche che si propagano
nell’aria tra due punti fissi (antenne).
Classificazione dei mezzi trasmissivi
Canali
Supporti fisici ad onde guidate
Ponti radio ad onde irradiate
Supporti metallici
Supporti non metallici
Fibre ottiche
Guide d’onda
Linee
In cavo
Aeree
Terrestri
Spaziali
( antenne)
( satelliti)
Caratteristiche dei canali di comunicazione
•La scelta del mezzo trasmissivo dipende dal tipo di segnale da trasmettere e quindi dalla
banda di frequenza. Nelle linee di trasmissione sia in cavo sia in aeree i segnali trasportati
sono di natura elettrica. Nelle fibre ottiche sono di natura diversa in quanto le
informazioni vengono trasmesse da sorgenti che emettono onde elettromagnetiche
luminose.
•La velocità di propagazione nei mezzi trasmissivi dipende dal tipo di mezzo impiegato,
ma maggiormente dipende dal tipo di isolamento utilizzato.
•Ad esempio per le linee a conduttori non isolati, nelle quali l’ isolante in questo caso è l’
aria, la velocità di propagazione è circa uguale alla velocità della luce, mentre per i
conduttori isolati la velocità di propagazione è più bassa.
Tipo di canale
Banda passante
(Hz)
Capacità del
canale (bit/sec)
Rapporto S/N
(dB)
Doppino telefonico
4 x 103
40 x 103
30
Fibre Ottiche
10 x 109
265 x 109
80
Guide D’onda
2 x 109
40 x 109
60
Ponti radio (2700
canali)
12 x 106
200 x 106
50
NOTA BENE
Esiste un legame tra la velocità e la frequenza del segnale dato dalla
seguente relazione:
λ= v/f
dove
λ:
rappresenta la distanza percorsa da un onda elettromagnetica in un
periodo e prende il nome di lunghezza d’onda ed è inversamente
proporzionale alla frequenza del segnale da trasmettere;
v: è la velocità di propagazione dell’onda sul mezzo trasmissivo;
f: è la frequenza del segnale propagato.
Rapporto segnale-rumore del canale
•Una delle caratteristiche più importanti dei canali è il rapporto segnale-rumore (S/N) il quale
indica la qualità di trasmissione.
•Per rapporto segnale-rumore si definisce come rapporto fra la potenza del segnale e la potenza
del rumore all’ uscita del quadripolo.
•Il rumore può essere suddiviso in:
•Rumore di origine esterna: è un segnale casuale costituito da picchi di breve durata. Le
principali cause sono le interferenze tra circuiti telefonici vicini, ecc… Il rumore di origine
esterne è a sua volta suddiviso in due categorie:
•Rumore atmosferico: causato da onde elettromagnetiche prodotte da scariche atmosferiche
naturali (fulmini)
•Rumore cosmico: causato da onde elettromagnetiche generate dai motori delle automobili,
ecc…
•Rumore di origine interna: si verifica all’ interno degli apparati stessi (resistori, circuiti
elettronici). Questo tipo di rumore è presente quasi sempre nei sistemi di comunicazione e non è
possibile eliminarlo.
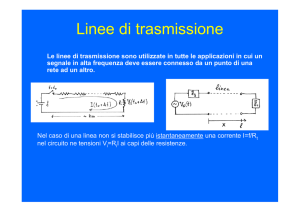
•Nel caso della nostra linea di trasmissione reale è necessario considerare più tratte della stessa
linea.
EFFETTO “PELLE”
L’Effetto Pelle fa variare la resistenza del conduttore al variare della frequenza.
Per capire in che cosa consiste tale effetto e da cosa dipende dobbiamo passare
attraverso le seguenti considerazioni teoriche:
1)Qualsiasi conduttore percorso da corrente variabile produce intorno a se un
campo elettrico variabile.
2)Quando esiste un campo elettrico variabile ci sarà necessariamente un campo
magnetico: si parla quindi di campo elettromagnetico.
3)Le linee di forza di tale campo saranno concatenate con il conduttore e
concentrate nell’intorno dell’asse dello stesso; le cariche in movimento saranno
quindi costrette a migrare negli strati più esterni: Effetto Pelle.
4)La sezione di passaggio delle cariche si riduce ad una corona sicuramente
minore rispetto all’intera sezione del conduttore e quindi, diminuendo tale sezione
di passaggio delle cariche, la resistenza del conduttore aumenta ( essendo S al
denominatore ) secondo la relazione:
R = * l / S
LINEE DI TRASMISSIONE A SUPPORTO
METALLICO
Le linee di trasmissione provvedono a trasferire segnali, sotto forma di
energia elettrica, o informazione, tra due posti distanti (generatore e carico).
La costituzione di questi mezzi è diversa in quanto dipende dall’impiego a cui
sono destinate.
GENERATORE
CARICO
La costituzione di questi mezzi dipende dall’impiego a cui sono destinate. Essi
attenuano i segnali che li percorrono e si comportano come dei quadripoli
passivi.
Due parametri fondamentali che interessano le linee di trasmissione sono:
COSTANTI PRIMARIE
COSTANTI SECONDARIE
COSTANTI PRIMARIE
Quando la linea è molto più corta di un quarto di lunghezza d'onda, pertanto
viene considerata a bassa frequenza e lo studio viene effettuato con le costanti
concentrate, mentre se la sua lunghezza è eguale o maggiore di un quarto di
lunghezza d'onda, la linea viene considerata ad alta frequenza e lo studio si
effettua con la teoria delle costanti distribuite.
Le costanti primarie fanno riferimento ai parametri resistivi e reattivi.
I parametri resistivi rappresentano la resistenza equivalente (R) e la
conduttanza equivalente (G) dovuta al non perfetto allineamento tra i
conduttori.
I parametri reattivi invece rappresentano l’ induttanza equivalente (L) e la
capacità equivalente (C).
La resistenza (R) e l’ induttanza (L) vengono chiamate costanti
longitudinali, la capacità (C) e la conduttanza (G) vengono chiamate
costanti trasversali.Tali costanti devono essere considerate lungo tutta la
linea e non in un punto soltanto della stessa.
Zl= R + jwL Impedenza Longitudinale
Yt= G + jwC Ammettenza trasversale
a) Resistenza kilometrica [W / m]
In generale la resistenza è definita dalla relazione
Dove:
r = resistività del conduttore e dipende dalla temperatura
l = lunghezza della linea [km]
S = sezione del conduttore [mmq]
La resistenza aumenta in modo proporzionale all’aumentare della frequenza a causa
del già esaminato effetto pelle.
b) Induttanza kilometrica [H / m] è data dal rapporto tra il flusso magnetico che
attraversa lo spazio fra i due conduttori della linea e la corrente che li percorre. Essa
dipende principalmente dal diametro dei conduttori e dalla loro distanza.
Per arrivare alla formula bisogna considerare un tratto di linea e
applicando ai suoi estremi una differenza di potenziale, all’ interno della linea ci sarà
una certa corrente che genererà un campo magnetico il quale anch’esso genera un
flusso che si concatena con il conduttore. Questo conduttore presenterà una certa
induttanza L che dipenderà solo dal flusso interno (Li).
Poiché la linea è costituita da due conduttori, si deve tener conto del campo
magnetico esterno che anch’esso dipenderà solo dal flusso esterno che viene generato
dal campo magnetico (Le).
Infine l’ induttanza kilometrica è data dalla somma delle due induttanze: esterna e
interna.
A frequenze elevate l’induttanza interna decresce a seguito dell’effetto pelle,
l’induttanza complessiva L è leggermente variabile in base alla frequenza.
c) Capacità Kilometrica [F / m] è quella equivalente a tutte le capacità presenti fra i
conduttori tra loro isolati e dipende dalla costante dielettrica del mezzo isolante fra i
due conduttori, dal loro diametro e dalla loro distanza.
d) Conduttanza Kilometrica [S / m] tiene conto della perdite che hanno luogo fra i
due conduttori per le imperfezioni dell’isolamento (perdita in corrente continua) e per
l’isteresi dielettrica (perdita in corrente alternata e dipende dalla frequenza).
In pratica la conduttanza rappresenta le correnti di dispersione esistenti tra i conduttori
e si calcola tramite la formula:
In questa espressione Go rappresenta la conduttanza che non dipende dalla
frequenza ed è l’inverso della resistenza di isolamento; Gf, invece, rappresenta la
conduttanza dipendente dalla frequenza.
In definitiva, le costanti primarie, variano al variare della frequenza e vengono
suddivise in funzione della loro indipendenza.
COSTANTI SECONDARIE
Lo schema a fianco ci fa
capire come queste tre
componenti sono correlate fra
loro e come la frequenza
influenzi le costanti primarie
e, di conseguenza, le
secondarie (che dipendono
dalle primarie).
COSTANTI
PRIMARIE
COSTANTI
SECONDARIE
FREQUENZA
Le costanti secondarie sono:
•l’impedenza caratteristica (Zo)
•la costante di propagazione (g).
e dipendono dall’impedenza longitudinale e dall’ammettenza trasversale, così prima
definite
Zl= R + jwL Impedenza Longitudinale
Yt= G + jwC Ammettenza trasversale
1) Zo =
2)  =
=
=
Inoltre essendo g un numero complesso, deve avere una parte reale a e una
immaginaria b:
 costante di attenuazione: è la parte reale e ci indica di quanto si
attenua il segnale ogni metro che avanza e si misura in Neper
/metro (o km), anche se la sua unità di misura più diffusa è il
decibel/metro - aumenta al crescere della frequenza (distorsione
di ampiezza).
 costante di fase: è la parte immaginaria ed indica di quanto
ruota la fase del segnale ogni metro che avanza e si misura
quindi in radianti/ metro (o km), anche se è pure misurata in
gradi/metro - varia in funzione della frequenza ( distorsione di
fase ).
N.B - Poiché la fase avanza di 2p radianti per ogni lunghezza d’onda l che
avanza, essa risulta:
2p=bl
VELOCITA’ DI PROPAGAZIONE
La velocità con cui si propagano queste onde è data per definizione dallo
spazio percorso s diviso il tempo t impiegato a percorrerlo, e cioè:
ma, essendo l lo spazio percorso dall’onda nel tempo T in cui avviene
un’oscillazione completa del segnale prodotto dal generatore, si ottiene,
sostituendo:
ma poiché è:
sostituendo risulta:
Moltiplicando numeratore e denominatore per 2p e ricordando che:
si ha:
La velocità così definita è chiamata velocità di propagazione dell’onda di
tensione e di corrente lungo la linea, e anche velocità di fase poiché rappresenta
la velocità con cui un osservatore deve spostarsi lungo la linea per vedere
sempre la stessa fase dell’onda.
LINEA NON DISTORCENTE
Esiste un caso particolare dove la costante di attenuazione è indipendente dalla
frequenza, cioè costante, e la costante di fase variabile linearmente con essa.Tale
condizione è data dalla seguente relazione RC = LG detta condizione di Heaviside, in
questo caso la linea risulterebbe non distorcente quindi ideale (senza
perdite).Certamente la condizione di Heaviside è da considerarsi ideale in quanto
RC>LG, si può tuttavia avvicinarsi alla condizione ideale tramite tecniche chiamate di
pupinizzazione che consistono nell’interporre lungo la linea delle bobine a intervalli
regolari (passo di pupinizzazione) le quali hanno il compito di aumentare l’induttanza
kilometrica che dipende dal valore delle bobine. I vantaggi di questo metodo è
l’attenuazione che diventa bassa e costante.
α
LINEA NON
PUPINIZZATA
LINEA
PUPINIZZATA
f
Richiami sulla
Distorsione di
ampiezza e di fase
EQUAZIONI GENERALI SULLA PROPAGAZIONE
Nell’analisi che segue, per determinare le equazioni differenziali che legano
tensione e corrente in ogni punto della linea, supponiamo di esaminare
inizialmente una porzione di linea dx molto più piccola di un quarto di
lunghezza d’onda e tale quindi da potersi studiare con la teoria delle costanti
concentrate.
Successivamente, estendendo la variazioni a tutta la lunghezza della linea, troveremo
le equazioni di propagazione che esprimeranno l’andamento della tensione Vx e della
corrente Ix lungo tutta la linea.
Ecco lo schema del tratto di
linea dx con le costanti
primarie (longitudinali e
trasversali)
Si supponga per semplicità, che il generatore di segnale sia di tipo sinusoidale e sia
x la distanza della sezione generica della linea dal generatore.
Dall’esame del circuito, applicando i due principi di Kirchhoff, si ha:
e, dividendo membro a membro per dx:
Queste equazioni esprimono il legame esistente fra la tensione, la corrente, e
le loro variazioni, lungo la linea in funzione delle costanti primarie R, L,
G, C, della linea.
Le soluzioni delle equazioni dei telefonisti e dei telegrafisti sono:
In cui:
è la costante di propagazione
è l’ impedenza caratteristica
Ambedue, come già visto, prendono il nome di costanti secondarie delle linee e sono,
come si può osservare, dei numeri complessi.
CONSIDERAZIONI SULLE EQUAZIONI GENERALI DI PROPAGAZIONE
Per comprendere meglio il significato fisico delle soluzioni delle equazioni dei Telefonisti,
è opportuno esaminare separatamente i termini a secondo membro delle due espressioni.
1) Matematicamente ciascuna delle due equazioni, che sono uguali nella struttura, è
costituita dalla somma di due funzioni matematiche “ESPONENZIALI”:
•
la prima ad esponente negativo, con ampiezza decrescente
•
la seconda ad esponente positivo, con ampiezza crescente
2) Ciascun termine esponenziale, matematicamente, rappresenta un vettore ruotante sul
piano (Re;Im)
N.B. il senso della rotazione dipende dal segno dell’esponente
3) Un vettore ruotante sul piano dell’immaginario rappresenta un segnale analogico,
variabile nel tempo.
4) Esaminiamo quindi separatamente i membri che costituiscono le equazioni:
•
I primi membri rappresentano, rispettivamente, un’onda di tensione ed una di
corrente che partendo dal generatore, percorrono tutta la linea fino al carico:
ONDE DIRETTE
•
I secondi membri rappresentano, rispettivamente, un’onda di tensione ed una
corrente che, partendo dal carico, percorrono la linea verso il generatore: ONDE
RIFLESSE
5) Esaminiamo il termine che rappresenta l’onda diretta di tensione
Essendo x la distanza generica dall’inizio della linea,
ponendo in questa formula x = 0, si ottiene la tensione
dovuta all’onda diretta all’inizio della linea:
V(0) = A = Vd
6) Analogamente analizzando il termine che rappresenta l’onda diretta di corrente per x=0,
si ottiene la corrente dovuta all’onda diretta all’ingresso in linea:
I(0) = A/Zo = Id
7) Il termine B invece rappresenta la tensione all’inizio della linea dovuta all’onda riflessa
ed il termine B/Z0 la corrente all’inizio della linea dovuta all’onda riflessa.
V(0) = B = Vr
I(0) = B/Zo = Ir
CONCLUSIONE: le equazioni generali della propagazione diventano
Onda diretta
V= Vd *
e-  x +
Vr * e
x
e-  x
Onda riflessa
ex
I= Id * e-  x + Ir * e x
GENERATORE
CARICO
Le quali equazioni ci dicono che la tensione o la corrente in un qualsiasi punto della
linea è data dalla somma vettoriale di due vettori ruotanti in senso opposto, il
primo detto onda diretta, decrescente dal generatore al carico, e l’altro onda
riflessa decrescente dal carico verso il generatore.
Inoltre i valori di tensione e corrente assumeranno, a seconda la posizione x lungo la
linea, valori compresi tra un massimo (quando Vd e Vr sono in fase) ed un minimo
(quando Vd e Vr sono in opposizione di fase ).
RICAPITOLANDO
SEGNALE DA
TRASMETTERE
ALTA
FREQUENZA
EQUAZIONI DI
PROPAGAZIONE
EFFETTO
PELLE
COSTANTI
PRIMARIE
COSTANTI
SECONDARIE
Le equazioni di propagazione, quindi sono equazioni matematiche che ci
permettono di conoscere l’uscita in funzione del segnale di ingresso.
CONDIZIONI DI PROPAGAZIONE LUNGO LA LINEA
Esistono due casi di propagazione: 1) Linea adattata  Regime Progressivo;
2) Linea disadattata  Regime Stazionario
Dipende dai valori di R0 ed RL
LINEA ADATTATA
Pd
Pa
In linea adattata cioè Ro=RL tutta la potenza viene assorbita dal carico abbiamo
quindi il massimo trasferimento di potenza e non abbiamo perdite cioè Pd=Pa siamo
in regime progressivo.
LINEA DISADATTATA
Pd
Pr
Pa
In linea disadattata cioè Ro≠RL la potenza non viene assorbita tutta dal carico cioè
Pd= Pr+Pa e vi saranno perdite di potenza.
In questo caso abbiamo la comparsa della potenza riflessa cioè Pr ovvero la perdita,
in questo caso ci troviamo in regime d’onda stazionario.
Lungo la linea avremo la presenza delle onde riflesse della tensione e della corrente.
COEFFICIENTE DI RIFLESSIONE
Essi ci danno l’idea del disadattamento del sistema e quantificano la percentuale
di tensione o corrente perse per riflessioni. Esso è dato dal rapporto vettoriale
fra il segnale riflesso e quello diretto, sia della tensione che della corrente:
Kv = Vr/Vd
e
Ki = Ir/Id
Il coefficiente di riflessione K è funzione dell’impedenza di carico ZL e
dell’impedenza caratteristica della linea Z0 secondo l’espressione:
Kv
Si può dimostrare che:
Kv = - Ki
Ki = - Kv
CASI PARTICOLARI
Dalla precedente relazione si possono fare le seguenti considerazioni:
1) Ro=RL  Ki=-Kv =0
allora il sistema è adattato
2) Se il carico è un cortocircuito: RL= 0  Kv=-Ro/Ro= -1 quindi KI=1
non c’è assorbimento di potenza in poche parole vi è una riflessione
totale
3) Se il circuito è aperto: RL = ∞  Kv = 1 quindi Ki = -1
anche in questo caso non c’è assorbimento di potenza, cioè si avrà
riflessione totale
Pertanto i valori che possono assumere i coefficienti di riflessione sono:
-1 < K I,V < 1
SIGNIFICATO FISICO DEL COEFFICIENTE DI RIFLESSIONE
Kv= Vr/Vd = +1
Il Segno (+)
Il valore (1)
Kv= Vr/Vd = -1
Il Segno (-)
l’onda riflessa dal carico è uguale in ampiezza all’onda diretta
quindi, quest’ultima è stata totalmente riflessa con la stessa
fase dell’onda diretta.
indica che l’onda riflessa nasce con la stessa fase dell’onda
diretta.
Il numero 1 indica la percentuale di segnale perso in
rapporto al segnale diretto.
l’onda riflessa dal carico è uguale in ampiezza all’onda diretta
quindi, quest’ultima è stata totalmente riflessa sfasata di 180°
rispetto all’onda diretta.
indica che l’onda riflessa nasce sfasata di 180° rispetto
all’onda diretta.
Esempio: Ki=0,6 ; Kv=-0,6
0,6 il 60% di segnale viene riflesso, mentre il restante 40% (0,4) viene assorbito
dal carico.
REGIME STAZIONARIO – L’ONDA STAZIONARIA
Le onde stazionarie (rispettivamente di tensione e corrente) nascono dalla
somma vettoriale dell’onda diretta e dell’onda riflessa.
Essa è costituita da un susseguirsi di valori
massimi (Vd + Vr) quando i due vettori sono in fase
minimi (Vd – Vr) quando i due vettori sono in opposizione di fase
L’onda stazionaria, essendo i valori di Vd o Id sempre maggiori rispetto a
Vr ed Ir, assumerà valori sempre positivi.
Essendo la fase tra i due vettori ruotanti dipendente dalla posizione x in cui ci
troviamo lungo la linea, l’onda stazionaria di tensione e di corrente,
rappresentano uno “stato” della linea stessa (non è un segnale che viaggia in
linea ma è una condizione in cui la linea si trova).
La forma dell’onda stazionaria di tensione o corrente presenta i valori massimi
piuttosto appiattiti mentre i valori minimi sono stretti. In condizioni limite, con
sistema completamente disadattato, il valore minimo assume valore 0.
Partendo dalla situazione in figura (condizione di massimo)
compiendo i due vettori una rotazione di soli 90° in senso opposto, si
troveranno in opposizione di fase e, pertanto in condizione di minimo;
Ad una ulteriore rotazione di 90° in senso opposto si ritroveranno in
fase e quindi in condizione di massimo.
Pertanto il periodo dell’Onda Stazionaria è di soli 180° cioè l/2.
Vd
Essendo Ki = -Kv se sul carico abbiamo un valore massimo dell’onda stazionaria di
corrente, avremo un valore minimo dell’onda stazionaria di tensione.
Pertanto le due onde stazionarie sono sfasate di 90° cioè l/4.
Vr
Kv = 1
Kv =-1
Kv = 1
Kv =-1
ROS RAPPORTO D’ONDA STAZIONARIA - SWR
SWR (in inglese: Standing Wave Ratio)
Per definizione
Legame tra K e ROS
ROS= Vmax/Vmin = Imax/Imin = 1+Kv/1-Kv
1< ROS < ∞
-1< K < 1
Kv = ROS-1/ROS+1
Il valore del ROS può variare fra uno e infinito al variare di K fra zero e uno.
Per una linea adattata, il ROS è uguale a uno, mentre nel caso di una linea chiusa in
corto circuito od aperta o con carico puramente reattivo, è infinito.
IMPEDENZA DI INGRESSO
L’impedenza in un punto qualsiasi della linea è definita come il rapporto fra la tensione e
la corrente in quel punto della linea, intendendo naturalmente come tensione, la tensione
totale, cioè la somma della tensione incidente più quella riflessa e come corrente, la
corrente totale.
Infatti uno strumento di misura come il voltmetro, non è in grado di distinguere se le
cariche elettriche che determinano quella tensione in quel punto siano venute da destra o
da sinistra.
L’impedenza allora, per una lunghezza “d” della linea, per quanto detto si ricava dalla
formula:
N.B. nella formula r = K
N.B. nella formula r = K
Per una linea senza perdite, essendo in questo caso: a = 0, e quindi: g = jb , e
ricordando che:
risulta, dopo molti passaggi che
per semplicità non si riportano:
Alcuni casi particolari:
1) l’impedenza di ingresso di un tratto di linea pari a l/2:
2) l’impedenza di ingresso di un tratto di linea pari a l/4:
Zl/2 = ZL
Zl/4 = Zo2/ZL
N.B. – quest’ultima formula ci aiuta a capire il comportamento di un tronco l/4
come adattatore di impedenza
ADATTAMENTO CON TRONCO l/4
Il disadattamento di una linea a radiofrequenza può
comportare parecchi inconvenienti.
Se il segnale prodotto dal generatore, viene in parte riflesso dal carico, una parte della
potenza sviluppata gli ritorna indietro sovraccaricandolo, ed eventualmente
distruggendolo, se non è stato dimensionato per sopportare questa nuova potenza che si
trasforma in calore.
Il caso peggiore si ha ovviamente nel caso del massimo disadattamento che si manifesta con
il carico in corto circuito o a circuito aperto.
Un trasmettitore, pertanto, non deve mai essere cortocircuitato ai piedi dell’antenna, ma
neanche deve essere staccata l’antenna mentre sta trasmettendo.
Lo stesso pericolo corre, a bassa frequenza, un amplificatore se si staccano le casse mentre
sta lavorando.
Inoltre un disadattamento d’antenna comporta, in ogni caso, una minore potenza trasmessa,
e quindi una minore portata del trasmettitore.
Quindi, fermo restando la potenza sviluppata dal generatore a radio frequenza, la portata
del trasmettitore viene drasticamente ridotta da un ROS troppo alto.
Si tollera un ROS di 1,2 – 1,5 ma mai valori superiori
Visti gli inconvenienti presentati dal disadattamento, si cercano delle tecniche per ridurre,
correggere o eliminare il disadattamento tra linea e carico.
Si può adattare un carico di tipo resistivo ad una linea inserendo un breve tratto di linea a
l/4 secondo lo schema della figura successiva:
Pertanto il nuovo schema del collegamento diventa:
Il dimensionamento
del troco l/4 avviene
in due fasi:
1) Calcolo della resistenza caratteristica del tronco, note quella della linea e la resistenza di
carico
2) I tronchi vengono realizzati in linea aerea con due fili paralleli: il valore già calcolato della
resistenza caratteristica viene raggiunto con opportuno dimensionamento della distanza “D” e
del diametro “d” dei conduttori ricordando che si ha:
R0’ = 276 log(D/d)
Avendo calcolato R0’, si ipotizza una delle due variabili “D” o “d” e si calcola l’altra,
con la formula inversa.
ADATTAMENTO CON STUB
Si può realizzare l’adattamento nel caso di carico costituito da resistenza e reattanza con uno
STUB, cioè un tratto di linea, dello stesso tipo di quella principale, ma collocata in
parallelo al carico in modo da eliminare la parte reattiva dell’impedenza e riducendola al
valore resistivo della resistenza caratteristica R0 della linea principale con l’aggiunta della
linea a l/4.
Il dimensionamento
dello STUB avviene
in due fasi:
1) Calcolo della POSIZIONE x dove piazzare lo STUB, imponendo che il tale punto la parte
reale dell’impedenza di linea deve coincidere con la resistenza caratteristica della stessa ;
2) Calcolo della reattanza dello STUB in quanto deve annullare la parte reattiva
dell’impedenza di linea nel punto dove è posizionato lo STUB.
I relativi calcoli si effettuano con la carta di SMITH.