L’ATOMO E I QUANTI DI ENERGIA
Relazione di
Elisa Colombo , Chiara Esposti , Chiara
Ferrari , Francesca Gallina , Rosa
Marchetti , Stefano Ponzoni , Laura
Riva , Michele Scotti , Martina Siena ,
Marco Travagliati .
I PRIMORDI DELL’ATOMO
Sebbene il concetto di atomo fosse già noto anche
nei secoli precedenti l’ottocento , tuttavia il suo
studio rientrava più nelle competenze della
filosofia. Ricordiamo , infatti , le teorie di Democrito
e Leucippo , fondatori della scuola atomista , o
successivamente quelle epicuree. Infatti la fisica
classica si concentrò per lo più sullo studio della
dinamica e della cinematica , utilizzando modelli
macroscopici e non soffermandosi su esperimenti
tesi a dimostrare l’esistenza dell’atomo e della sua
struttura.
LA CRISI DELLA FISICA
CLASSICA
Con l’aprirsi di alcune “crepe” nel sistema della
fisica classica , che non riusciva a spiegare
fenomeni come la radioattività o il secondo
principio della termodinamica , si avvertì
l’esigenza di indirizzare la sperimentazione
verso modelli microscopici , con i quali studiare
l’essenza particellare della natura e verificare
l’esistenza di unità subatomiche costituenti la
materia.
EVOLUZIONE DEL CONCETTO DI ATOMO
La prima disputa si aprì tra i laboratori di
Thomson ed Hertz : riscontrando fenomeni di
luminescenza in un esperimento realizzato con
un tubo sigillato contenente gas al quale è stata
applicata una determinata differenza di
potenziale, sono state formulate due teorie
discordanti. Secondo Thomson si trattava di un
flusso di particelle materiali , mentre Hertz
sosteneva fossero raggi . Prevalse la prima teoria.
IL MODELLO DI THOMPSON
Una seconda disputa si aprì
nuovamente tra la stessa
teoria di Thomson e quella
elaborata da Rutherford a
proposito della struttura
atomica per giustificarne la
neutralità e la stabilità. Il
modello di Thomson , noto
come “a panettone” ,
prevedeva che la carica
positiva si trovasse
distribuita all’interno
dell’atomo come in una nube.
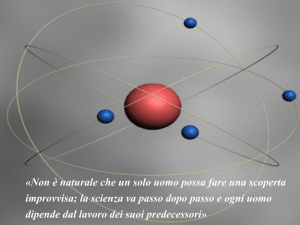
IL MODELLO DI RUTHERFORD
Rutherford sosteneva che la
carica positiva fosse
concentrata interamente nel
centro dell’atomo e che gli
elettroni descrivessero
attorno ad esso traiettorie
ellittiche. Grazie alla
rilevazione del fenomeno del
back-scattering e , solo pochi
anni più tardi , alla prima
memoria di Bohr , questo
modello è stato qualificato
come il più attendibile.
IL MODELLO DI BOHR
Bohr perfeziona il modello di
Rutherford il cui grande
limite riguardava il
movimento disordinato
degli elettroni , che
avrebbero dovuto
progressivamente
avvicinarsi al nucleo
positivo , sino ad annullarsi.
Secondo la nuova teoria di
Bohr questi si muovevano
lungo orbite stazionarie non
emettendo energia.
Breve scheda su Thomson
Nel 1897, J. J. Thomson dimostrò che i raggi sconosciuti
presenti nel catodo erano particelle cariche
negativamente - egli aveva scoperto gli elettroni. Nello
stesso anno egli calcolò il rapporto tra la carica e la
massa dell’elettrone (e/m) determinando la prima misura
di una costante fondamentale.
Introduzione all’esperimento
L’esperimento di Thomson si inserisce nel
dibattito di fine ottocento volto a
determinare la natura e le proprietà della
materia. Thomson determina il rapporto
e/m di una particella che verrà definita
elettrone aprendo la strada a successivi
studi sulla materia in grado di spiegare
talune contraddizioni emerse dagli studi
degli scienziati della fisica classica.
Strumentazione
Ampolla di vetro con
elio a bassa pressione
Catodo riscaldato
Anodo forato
Bobine di Helmholtz
Indice graduato
riflettente
Descrizione dell’esperimento
All’interno dell’ampolla viene immesso elio a bassa
pressione quindi rarefatto
Il catodo viene riscaldato e gli elettroni della placca
metallica vengono liberati e si crea un campo elettrico.
Gli elettroni quindi escono dall’anodo forato.
Viene fornita corrente continua alle due bobine e si crea
un campo magnetico uniforme perpendicolare alla
traiettoria del fascio di elettroni.
Per effetto della forza di Lorentz gli elettroni vengono
deviati dal campo magnetico descrivendo una
circonferenza.
Dati
sx
r
0,036
0,039
0,04
0,043
0,044
0,045
0,045
0,048
sx
T (v)
0,0295
0,0325
0,0345
0,0365
0,038
0,039
0,0395
0,0415
r
0,04
0,041
0,044
0,046
0,048
0,051
0,053
1,75E+11
I (A)
175
225
250
275
300
325
350
375
T (v)
0,0345
0,0355
0,038
0,0405
0,042
0,0455
0,048
200
200
200
200
200
200
200
media delle medie scarto %
1,81253E+11
3,6%
2
2
2
2
2
2
2
2
media
dev. st
err. %
V/r^2
2,011E+05
2,130E+05
2,100E+05
2,064E+05
2,078E+05
2,137E+05
2,243E+05
2,11E+05
2,11E+05
6,8E+03
3,2%
e/m
1,65263E+11
1,75064E+11
1,72617E+11
1,6964E+11
1,7074E+11
1,75604E+11
1,84355E+11
1,78943E+11
1,74E+11
5,9E+09
3,4%
I (A)
1,8
1,7
1,6
1,5
1,4
1,3
1,2
media
dev. st
err. %
r^2I^2
3,856E-03
3,642E-03
3,697E-03
3,691E-03
3,457E-03
3,499E-03
3,318E-03
3,59E-03
1,8E-04
5,0%
e/m
1,70486E+11
1,80516E+11
1,77854E+11
1,78147E+11
1,90159E+11
1,87915E+11
1,98164E+11
1,83E+11
9,3E+09
5,1%
Intensità
costante
Tensione
costante
Come calcolare e/m
1 2
eDV = mv
2
mv 2
= qvB
ma =
R
2DV
q
=
2
m (KIR )
ESPERIENZA DI RUTHERFORD
Scopo dell’esperienza
Studiare la struttura interna dell'atomo: conferma del modello planetario
di Rutherford.
Modello di Rutherford
a) la carica positiva è concentrata nel nucleo atomico di dimensioni
ridotte rispetto al volume occupato dall’atomo e di elevata densità
b) le cariche negative ruotano su orbite esterne al nucleo
Modello di Thomson
a)l’atomo viene considerato come una nube atomica con carica positiva
distribuita in modo continuo sull’intero volume
b)all’interno di tale regione si muovono le cariche negative
ESPERIENZA DI RUTHERFORD
Materiale utilizzato
Apparato sperimentale costituito da una camera a vuoto contenente una
sorgente di particelle indirizzata contro la lamina d’oro. Alla
superficie superiore della camera è collegato il rilevatore di particelle a
semiconduttore in grado di ruotare a diverse angolazioni .
ESPERIENZA DI RUTHERFORD
Angolo (°)
-15
-12,5
-10
-7,5
-5
-2,5
0
2,5
5
7,5
10
12,5
15
PROVA 1
tempo (s) conteggi (n)
n/t
180
1228
6,822
160
3159
19,744
140
4259
30,421
100
4623
46,230
80
4278
53,475
60
3401
56,683
60
3212
53,533
60
3135
52,250
80
3762
47,025
100
3645
36,450
140
3347
23,907
160
1794
11,213
180
958
5,322
Prova n°1: risultati
sperimentali
ESPERIENZA DI RUTHERFORD
Angolo (°)
-20
-17,5
-15
-12,5
-10
-7,5
-5
-2,5
0
2,5
5
7,5
10
12,5
15
17,5
20
PROVA 2
tempo (s) conteggi (n)
n/t
360
271
0,753
330
848
2,570
300
1857
6,190
270
5173
19,159
240
8315
34,646
210
10439
49,710
180
9803
54,461
150
8310
55,400
120
6586
54,883
150
7415
49,433
180
8235
45,750
210
7558
35,990
240
5294
22,058
270
2648
9,807
300
1516
5,053
330
740
2,242
360
335
0,931
Prova n°2: risultati
sperimentali
ESPERIENZA DI RUTHERFORD
Calcolo dell'errore
100
media 1-2
Errore media
0,753
2,570
6,506
0,316
19,452
0,292
32,534
2,112
47,970
1,740
53,968
0,493
56,042
0,642
54,208
0,675
50,842
1,408
46,388
0,637
36,220
0,230
22,983
0,924
10,510
0,703
5,188
0,134
2,242
0,931
90
80
70
60
50
40
30
20
10
0
-25
-20
-15
-10
-5
0
5
10
15
20
25
Prova 1
Prova 2
Curva teorica
ESPERIENZA DI RUTHERFORD
Conclusioni ed osservazioni
Abbiamo verificato che per angoli di ampiezza superiore a
12°30’ i risultati sono compatibili con la relazione di
Rutherford.
n() = C (sen4 /2 ) -1
Risulta inaccettabile il modello di Thomson in quanto è stato
osservato il fenomeno di back-scattering.
SPETTRI DI EMISSIONE
Strumentazione:
Lampada al mercurio
Focalizzatori
Reticolo di diffrazione
Sensori
L’ESPERIMENTO
Descrizione:
la radiazione luminosa della lampada a
mercurio produce, una volta diffratta, uno
spettro di righe colorate.
SIMMETRIA
FENDITURE
Confronto tra diverse
fenditure:
•fenditura più piccola = minor
intensità
•fenditura più grande =
maggior numero di picchi
NEON VS MERCURIO
MODELLO ATOMICO DI BOHR
POSTULATI DI BOHR
L’idea di atomo:
fisica classica + 2 ipotesi
•Le orbite stazionarie sono caratterizzate
da un momento angolare dell’elettrone
uguale a un multiplo intero della costante
di Planck
L = n h/2p
•La transizione di un elettrone tra orbite
stazionarie è accompagnata dall’emissione
di radiazione la cui frequenza n è legata
all’energia iniziale E1 e a quella finale E2
dalla relazione
E2 - E1 = hn
Gli spettri
Se si fornisce energia ad un elettrone, questo è in grado di emettere, sotto
forma di radiazione luminosa, questa stessa energia, tornando nel suo stato
fondamentale.
Gli spettri
Già noti ma non
completamente
spiegabili con la fisica
classica
La serie di Balmer
1/l = R (1/4 - 1/n2)
GENERALIZZATA
R (1/m2 - 1/n2)