COGNOME _________________________ NOME ______________________
CLASSE ______________________ DATA _________________________
Scheda 3
COME SI MUOVE UNA FILA DI RUOTE INGRANATE?
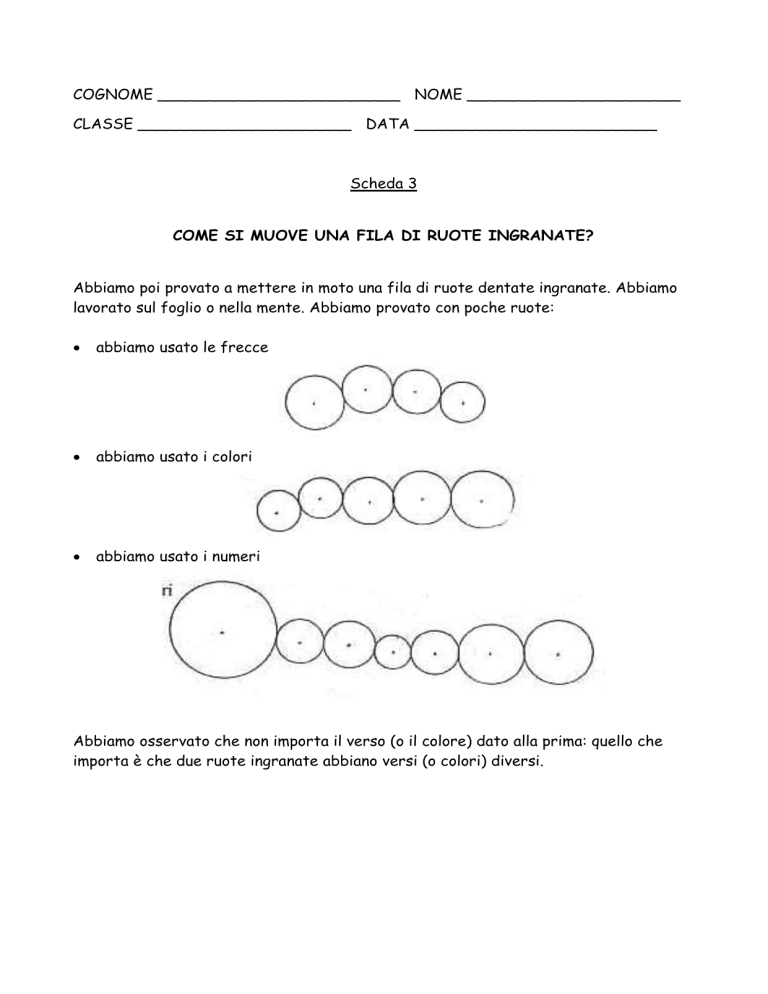
Abbiamo poi provato a mettere in moto una fila di ruote dentate ingranate. Abbiamo
lavorato sul foglio o nella mente. Abbiamo provato con poche ruote:
abbiamo usato le frecce
abbiamo usato i colori
abbiamo usato i numeri
Abbiamo osservato che non importa il verso (o il colore) dato alla prima: quello che
importa è che due ruote ingranate abbiano versi (o colori) diversi.
Abbiamo concluso che:
SE UNA FILA CONTIENE UN NUMERO PARI DI RUOTE DENTATE LA PRIMA E
L'ULTIMA GIRANO IN VERSI OPPOSTI.
SE UNA FILA CONTIENE UN NUMERO DISPARI DI RUOTE DENTATE LA PRIMA
E L'ULTIMA GIRANO NELLO STESSO VERSO.
Lo DIMOSTRIAMO facendoci prestare le parole da Erone
Se la prima ruota si muove col verso contrario a quello della seconda (e la seconda col
verso contrario a quello della prima), il movimento della prima sarà lo stesso che quello
della terza.
Se poi c'è una quarta ruota, si farà la stessa dimostrazione.
Riassumendo, quello che si ha con tre ruote si ripete per tutte le file di ruote in
numero dispari, e quello che si ha per due ruote di ripete per tutte le file in cui le
ruote sono accoppiate a due a due (cioè sono in numero pari).
Con questo ragionamento possiamo PREVEDERE il verso di rotazione dell'ultima ruota
di una fila di ruote anche molto lunga, SENZA METTERLE IN MOTO DAVVERO:
basta sapere se sono in numero pari o in numero dispari.
numero pari - verso opposto
numero dispari - stesso verso