MATURITA’ 1998
Disegni a cura del prof. Cristiano DOMENICHELLI
Testi della prof.ssa Tiziana LA TORELLA
LICEO SCIENTIFICO “GALILEO FERRARIS
1
ESAME DI STATO DI LICEO SCIENTIFICO
CORSO DI ORDINAMENTO
Sessione 1998
Indirizzo: SCIENTIFICO
Tema di : MATEMATICA
Un cateto di un triangolo rettangolo è lungo 2a, dove a è una lunghezza nota, e l’angolo acuto
adiacente ad esso ha coseno uguale a
.
a) Condotta per il vertice dell’angolo retto una retta t che non attraversa il triangolo e indicata
con x la misura dell’angolo che questa retta forma col cateto maggiore, esprimere in funzione
di x il volume V(x) del solido generato dal triangolo quando compie una rotazione completa
intorno alla retta t.
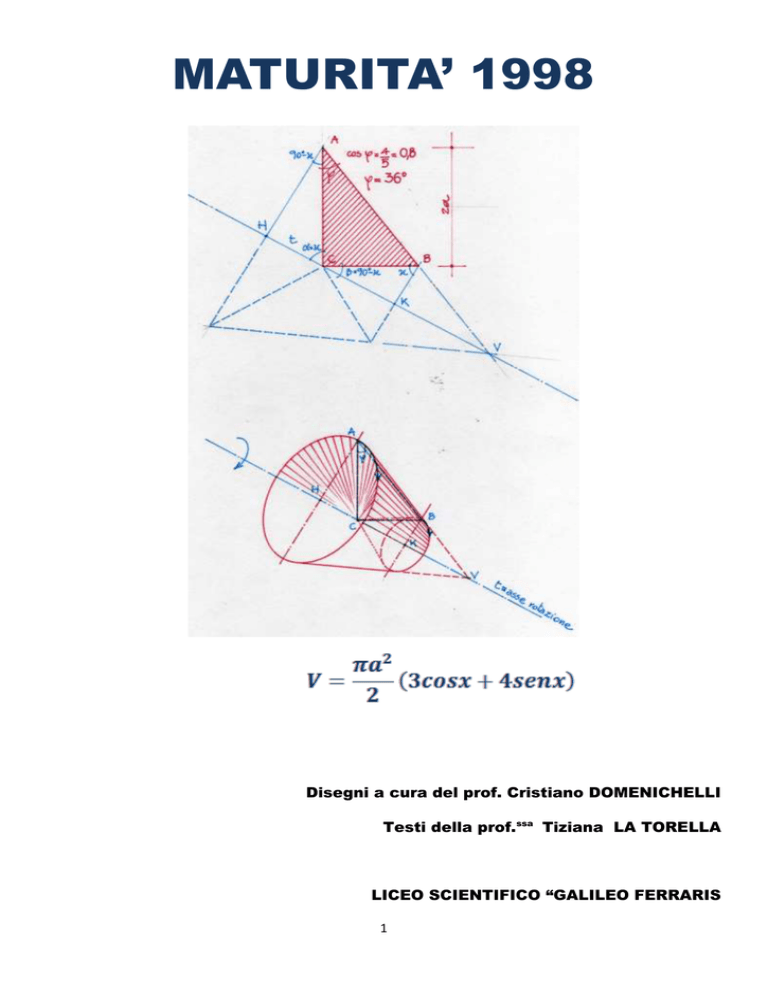
b) Verificato che risulta:
V( x )
1 3
a ( 4 sen x 3 cos x ),
2
con x appartenente ad un determinato intervallo, studiare la funzione V(x) nell’intervallo
stabilito e disegnarne il grafico in un piano cartesiano.
c) Utilizzare il grafico disegnato per determinare x in modo che il volume del solido di rotazione
descritto sopra sia kπa3, dove k è un parametro reale assegnato.
d) Completare la risoluzione dimostrando, col metodo preferito, che il volume V di un tronco di
cono di raggi R ed r ed altezza h è espresso dalla seguente formula:
V
1
h ( R 2 r 2 Rr )
3
Breve spiegazione
Il problema presenta più argomenti distinti in ambiti diversi:
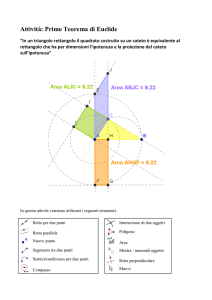
a) Si applica la trigonometria per determinare i lati del triangolo rettangolo iniziale ABC e dei due
triangoli AHC e CKB, le cui rotazioni intorno alla retta t genereranno due coni.
Si considera la geometria solida e si costruisce un solido di rotazione definito da un tronco di cono al
quale sono stati sottratti due coni. Si calcola il volume
del solido ottenuto.
b) L’analisi permette lo studio della funzione trigonometrica
c) Si trovano le intersezioni tra il grafico della curva
discute il sistema.
d) Si dimostra la formula del volume di un tronco di cono .
2
.
e della retta orizzontale
kπa3 e si
Un cateto di un triangolo rettangolo è lungo 2a, dove a è una lunghezza nota, e l’angolo
acuto adiacente ad esso ha coseno uguale a
.
a) Condotta per il vertice dell’angolo retto una retta t che non attraversa il triangolo e
indicata con x la misura dell’angolo che questa retta forma col cateto maggiore, esprimere
in funzione di x il volume V(x) del solido generato dal triangolo quando compie una
rotazione completa intorno alla retta t.
L’angolo x , compreso tra il cateto maggiore del triangolo ABC e la retta t, varia tra 0° e 90°
perché non deve attraversare il triangolo.
3
Si applicano i teoremi relativi al triangolo rettangolo ABC per determinare
L’ipotenusa AB:
Il cateto minore BC:
I raggi AH e BK delle basi del tronco di cono :
Le altezze dei coni ACH e BCK :
L’altezza HK del tronco di cono
4
Il volume del solido di rotazione è una differenza di volumi
Ricordando la formula del tronco di cono :
V
1
h ( R 2 r 2 Rr )
3
punto a)
5
b) Verificato che risulta:
V( x )
1 3
a ( 4 sen x 3 cos x ),
2
con x appartenente ad un determinato intervallo, studiare la funzione V(x)
nell’intervallo stabilito e disegnarne il grafico in un piano cartesiano.
Punto b)
6
c) Utilizzare il grafico disegnato per determinare x in modo che il volume del solido di
rotazione descritto sopra sia kπa3, dove k è un parametro reale assegnato.
E’ la soluzione del sistema
La discussione presenta la seguente soluzione grafica :
e
. punto c)
d)
Si dimostra la formula del volume di un tronco di cono come differenza di volumi.
1
V h ( R 2 r 2 Rr )
3
7
punto d)