Divisibilità tra polinomi

2aC - PROVA DI ALGEBRA
28-sett-2055
Es1) Semplifica le espressioni.
4
2 
2 


a)  a  b   a  a  b 
3 
3 


3
1
1
1   1

 2
 2
 1

 x  x  6 x  5x  6 x  9   x  2


b) 
2
1
 1
1

x
c)  x

1

x
1 
x



 x 3 x 2





x
b
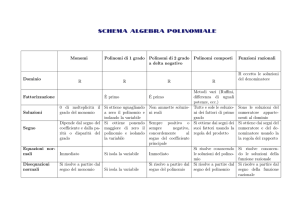
Es2) Determina l’area complessiva della figura, costituita da tre quadrati.
(i dati sono sul disegno; il polinomio che esprime l’area va messo in
forma normale)
a
Es3) Calcola MCD e MCM dei seguenti polinomi
4x 3  4x 2  x
2x 3  x 2  2x  1
Es4) Quali dei seguenti polinomi è divisibile sia per
A)
x 3  3x  2
B)
x 3  x 2  4x  4
2x 3  3x 2  x
x  2 che per x  1 ?
C)
x 4  5x 2  4
D)
x 3  2x 2  x  2
Trova la scomposizione in fattori di tali polinomi.
Es5) Verifica che togliendo 5 alla somma dei quadrati di quattro numeri interi consecutivi qualunque si ottiene un
quadrato.
Es6)
a) Determina il resto della divisione tra il polinomio
ed il polinomio
f ( x )  x 10  x 9  x 8  ...  x 2  x  1
x 1
b) Generalizzando, stabilisci una legge che associ al grado n del polinomio
f ( x )  x n  x n 1  x n 2  ...  x 2  x  1
il resto della divisione tra il polinomio ed il polinomio
x 1