problema-risolto-con

Problema
In un sistema di riferimento cartesiano Oxy sono date le due rette
r ed s di equazione, rispettivamente, y=1 e y=-k, dove k è un
parametro reale positivo.
a)Indicati con P il punto di r di ascissa
di ascissa k/√3, determinare
triangolo OPQ.
1/√3 e Q il punto di s
la circonferenza  circoscritta al
b)Scrivere in funzione di k:
 le coordinate del centro C
 il valore del raggio r
 l’equazione di 
 le coordinate del punto S, diverso da O in cui incontra
l’asse x e del punto R diverso da P in cui incontra la
retta r
c) Verificare che per qualunque valore
di k :
 il quadrilatero OPRQ è un trapezio isoscele
 il triangolo PQS è equilatero
d)Determinare la posizione limite , al tendere di k a 0 :
 del centro C
 della circonferenza 
La risoluzione del problema si trova nella PAGINA :Problemi di Matematica con
soluzione
Sotto-Pagina
Geometria Analitica
File Problema sulla circonferenza
Costruzione della figura con Geogebra
 Definire il numero k come slider , con valore min. 0 e valore max 10
 Definire la retta r y=1
 Definire i punti
O=(0,0) P=(1/sqrt(3) , 1)
Q=(k/sqrt(3), -k)
 Definire i segmenti OP e OQ
 Costruire gli assi dei suddetti segmenti
 Definire C, intersezione dei due assi
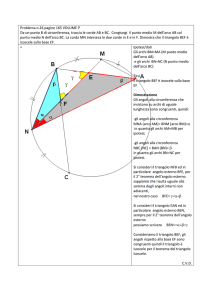
 Costruire la circonferenza di centro C passante per O
 Osservare che la circonferenza passa per P e per Q
( per costruzione C deve essere equidistante da O, da P e da Q)
 Definire i punti R ed S ( intersezioni della circonferenza con la retta y=1 e
con l’asse x)
 Far variare il valore di k e osservare le diverse figure
Con lo strumento angolo evidenziare l’ampiezza dell’angolo S Q
Osservare che al variare di k varia la posizione di Q, ma non quella della
retta OQ, in quanto l’angolo evidenziato ha sempre ampiezza 60°
QUADRILATERO
 Costruire il poligono OPQR
 Con lo strumento angolo evidenziare le ampiezze degli angoli e verificare
che il quadrilatero è un trapezio isoscele
 Far variare il valore di k e osservare le diverse figure
Per qualunque valore di k il quadrilatero è un trapezio isoscele avente due angoli,
adiacenti alla base minore , di 120° e gli altri due di 60°.
TRIANGOLO
 Costruire il poligono PQS
 Con lo strumento angolo evidenziare le ampiezze degli angoli e verificare che il
triangolo è equilatero
 Far variare il valore di k e osservare le diverse figure
Gli angoli interni del triangolo PQS hanno sempre ampiezza 60°, quindi il triangolo
è equilatero
POSIZIONE LIMITE
Spostare il valore di k sullo slider in modo da fargli assumere valori vicino allo 0
Per k = 0 la figura perde di significato, ma per valori prossimi a 0 la circonferenza tende assumere la
configurazione tangente in O alle retta OQ