Martedì 06 maggio 2008 - Fisica Generale II ing. Civile - dr. Lenisa
Esercizio 1
Determinare l’accelerazione del centro di massa di una sfera omogenea di massa m e raggio R che
rotola senza strisciare su di un piano inclinato di un angolo rispetto all’orizzontale. Si calcoli
l’accelerazione nelle stesse condizioni per un cilindro di raggio ed un anello anch’esso di raggio R.
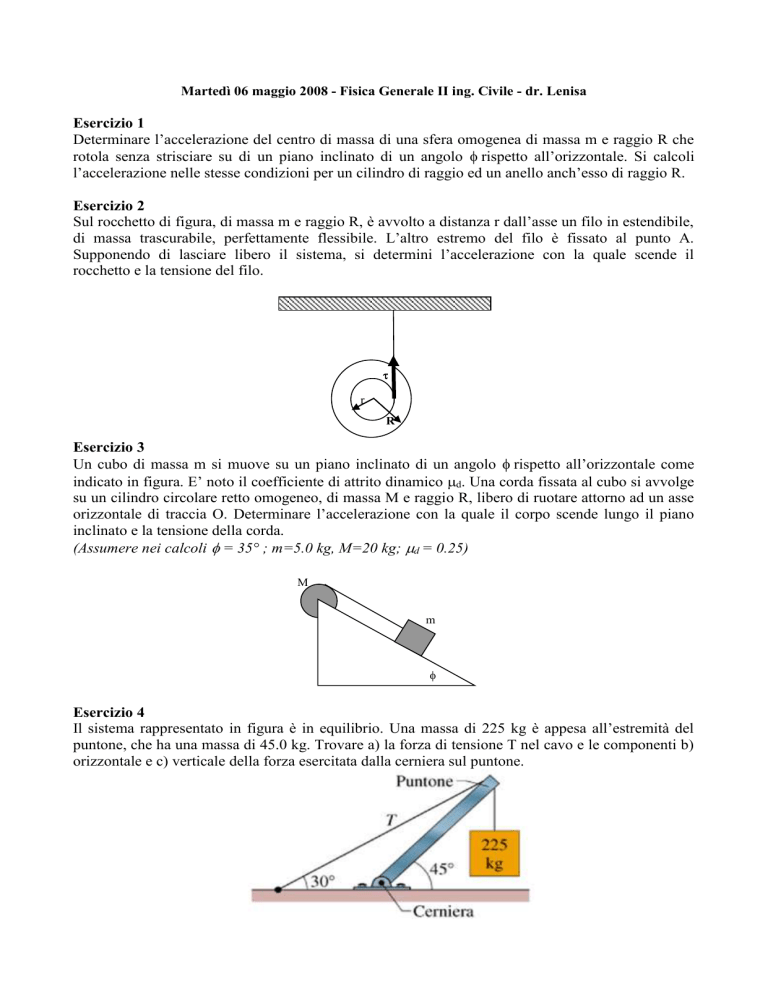
Esercizio 2
Sul rocchetto di figura, di massa m e raggio R, è avvolto a distanza r dall’asse un filo in estendibile,
di massa trascurabile, perfettamente flessibile. L’altro estremo del filo è fissato al punto A.
Supponendo di lasciare libero il sistema, si determini l’accelerazione con la quale scende il
rocchetto e la tensione del filo.
r
R
Esercizio 3
Un cubo di massa m si muove su un piano inclinato di un angolo rispetto all’orizzontale come
indicato in figura. E’ noto il coefficiente di attrito dinamico d. Una corda fissata al cubo si avvolge
su un cilindro circolare retto omogeneo, di massa M e raggio R, libero di ruotare attorno ad un asse
orizzontale di traccia O. Determinare l’accelerazione con la quale il corpo scende lungo il piano
inclinato e la tensione della corda.
(Assumere nei calcoli = 35° ; m=5.0 kg, M=20 kg; d = 0.25)
M
m
Esercizio 4
Il sistema rappresentato in figura è in equilibrio. Una massa di 225 kg è appesa all’estremità del
puntone, che ha una massa di 45.0 kg. Trovare a) la forza di tensione T nel cavo e le componenti b)
orizzontale e c) verticale della forza esercitata dalla cerniera sul puntone.
Venerdì 09 maggio 2008 - Fisica Generale II ing. Civile - dr. Lenisa
Esercizio 1
La puleggia di figura può ruotare senza attrito attorno al proprio asse. Essa è assimilabile ad un cilindro retto omogeneo
di raggio R e massa M. Il filo, di massa trascurabile, porta agli estremi due corpi puntiformi rispettivamente di massa m 1
e m2 e fa ruotare la puleggia senza scivolare su di essa. Nell’ipotesi che le due masse si muovano con accelerazione a, si
determinino le tensioni 1 e 2 di ciascuno dei due tratti di filo e la massa M della puleggia.
(Si effettuino i calcoli assumendo m1=2m2=2.00 kg; a=1.45 m/s2)
1
M
2
m2
m1
Esercizio 2
Sul rocchetto di figura, di massa m e raggio R, è avvolto a distanza r dall’asse un filo in estendibile, di massa
trascurabile, perfettamente flessibile. L’altro estremo del filo è fissato al punto A. Supponendo di lasciare libero il
sistema, si determini l’accelerazione con la quale scende il rocchetto e la tensione del filo.
Esercizio 3
Un’asta rigida filiforme, di massa M e lunghezza l, è incernierata all’estremo O in modo da poter ruotare liberamente
nel piano verticale. Un proiettile di massa m, dotato di velocità v0 orizzontale, colpisce l’asta a distanza d dalla cerniera.
Sapendo che l’asta devia dalla verticale di un angolo e che il proiettile, subito dopo l’urto, cade lungo la verticale si
determini la velocità v0 posseduta dal proiettile prima dell’urto.
(Assumere nei calcoli M=1.0 kg; l= 50 cm; m=1/10M; d=30 cm; =/6)
d
v0











