Matematica Discreta
Lezione del giorno 26 gennaio 2011
Numeri primi
Sia a un qualunque numero naturale. Dall’eguaglianza a=a•1 segue che a,1 sono in ogni caso
divisori di a (detti divisori banali di a).
Definiamo numero primo un numero naturale a>1 i cui unici divisori sono i divisori banali 1,a .
Nota: osserviamo che, nella definizione di numero primo, il numero naturale 1 non è considerato
primo. Il motivo di questa esclusione del numero 1 dai numeri primi sarà chiarito nella
dimostrazione del “Teorema di fattorizzazione unica”.
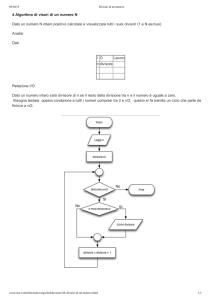
Per verificare se un numero naturale a>1 è primo o non lo è, un test “ingenuo” (poco efficiente)
consiste ovviamente nell’esaminare tutti i numeri naturali x compresi fra 2 e (a-1), e per ognuno di
tali x testare se esso è divisore o no di a (cioè dividere a per x e verificare se il resto è 0): se nessun
valore x fra 2 ed (a-1) è divisore di a, si conclude che a non ha divisori non banali, quindi a è primo;
se qualche valore x compreso fra 2 ed (a-1) è divisore di a, si è trovato un divisore non banale di a, e
si conclude quindi che a non è primo.
Si devono dunque effettuare (nel caso peggiore) a-2 divisioni.
Esempio:
Dato il numero a=1009, non si trova nessun valore x con x=2,3,4,….,1008, che sia divisore di x
(effettuando 1007 divisioni). Quindi a=1009 è primo.
Nota: nell’agosto del 2008 è stato trovato il più grande numero primo attualmente conosciuto (esso
ha quasi 13.000.000 cifre in base 10).
Utili notizie possono essere trovate sul sito www.mersenne.org
L’efficienza dell’algoritmo “ingenuo” illustrato nella lezione precedenza (per testare se un numero
naturale a è primo) può essere migliorata con la seguente osservazione: se un numero naturale a>1
non è primo, allora a ha certamente almeno un divisore non banale che sia a (infatti se a non è
primo, allora a ha un divisore non banale b1, ba, ed esiste un numero naturale c tale che a=bc,
con c1, ca: da ciò si deduce che almeno uno dei divisori b,c è a perché se fosse per assurdo
b> a , c> a si avrebbe bc>( a )2=a contraddizione).
Dunque per testare se a è primo, basta eseguire le divisioni di a per i valori 2,3,….. che siano a :
se nessuno di tali valori è un divisore di a allora si può concludere con certezza che a è primo,
operando un numero di divisioni molto inferiore.
Per esempio, se a=1009, invece di effettuare 1007 divisioni si possono effettuare le 30 divisioni di
a=1009 per i numeri 2,3,…..,31 (tenendo conto che 1009 è circa 31,76), e poiché ognuna di esse
ha resto diverso da 0 si può concludere che a=1009 non ha divisori non banali ed è dunque primo.
Anche questo test “ingenuo” migliorato ha però tempi di calcolo troppo lunghi nel caso di numeri
molto “grandi”: per esempio se l’ordine di grandezza del numero a da testare è circa 10 40 (1 seguito
da 40 zeri in base 10), l’ordine di grandezza di a è circa 1020, e se un computer potesse eseguire 1
miliardo di divisioni al secondo, il numero di secondi impiegati nell’esecuzione dell’algoritmo
sarebbe dell’ordine di grandezza di circa 1011 (oltre 3000 anni…….).
Per questo sono stati introdotti test molto più efficienti per verificare se un numero naturale è primo,
ma questo è un argomento che esula dagli scopi del nostro corso.
Basti osservare che per testare il numero primo più grande attualmente conosciuto (citato sopra, con
13 milioni di cifre in base 10) è bastato circa 1 mese di calcoli su un computer dotato di un
processore con una velocità di 3 Ghz.
Fattorizzazione in primi
Dimostreremo che i numeri primi sono come i “mattoni” elementari con cui si possono “costruire “
tutti i numeri naturali >1, nel senso che ogni naturale >1 è prodotto di numeri primi e tale
rappresentazione è sotto certi aspetti “unica”. Ricordiamo che per convenzione il termine
“prodotto” si intende al limite anche con 1 solo fattore.
Premettiamo un risultato preliminare sui numeri primi:
Teorema.
Se a è un numero primo e se a é divisore del prodotto di 2 numeri naturali b,c:
a (bc)
allora a è divisore di almeno uno dei fattori b,c.
Dimostrazione:
Per assurdo supponiamo che a non sia divisore né di b né di c.
Essendo a (bc) esiste un numero naturale t tale che at=bc.
Poniamo d=mcd(a,b). Essendo da, db ed essendo a numero primo, si ha d=1 oppure d=a. Ma non
può essere d=a (perché d è divisore di b mentre a non lo è) dunque è d=1. Per una proprietà del
mcd(a,b), esistono 2 interi relativi x, y tali che d=1=ax+by. Moltiplicando ambo i membri per c e
tenendo conto che at=bc si ha:
c=acx+bcy=acx+aty=a(cx+ty)
e si ottiene ac (contraddizione).
Dimostreremo ora un risultato fondamentale dell’aritmetica.
Premettiamo un’ooservazione.
Osservazione. Abbiamo già dimostrato il seguente: risultato:
se un numero primo a è divisore di un prodotto bc di 2 numeri naturali b,c, allora a è divisore di
almeno uno dei 2 fattori b,c.
Tale risultato si può estendere facilmente al caso del prodotto di 3 o più fattori.
Per esempio se il numero primo a è divisore di un prodotto bcd di 3 numeri naturali b,c,d allora,
utilizzando la proprietà associativa del prodotto, si può osservare che a sarà divisore del prodotto
(bc)d di 2 fattori bc,d dunque (utilizzando la proprietà precedente valida per 2 fattori) si otterrà
a(bc) oppure ad, e di nuovo applicando la proprietà precedente sarà ab oppure ac oppure ad,
quindi a sarà divisore di almeno uno dei 3 fattori b,c,d.
Con ragionamenti analoghi (oppure più formalmente ragionando per induzione) si ottiene che se un
numero primo a è divisore del prodotto di n numeri naturali, allora a è divisore di almeno uno dei
fattori (qualunque sia il numero n di fattori).
Teorema di fattorizzazione unica. Ogni numero naturale a>1 è fattorizzabile come prodotto di
numeri primi (al limite con 1 solo fattore) e tale fattorizzazione è unica (a meno dell’ordine dei
fattori), nel senso che, se sono date 2 fattorizzazioni dello stesso a in prodotto di numeri primi:
a=p1p2….pr=q1q2…qs (dove tutti i pi e i qj sono numeri primi)
allora:
1) r=s (il numero dei fattori primi nelle 2 fattorizzazioni è uguale)
2) riordinando opportunamente i fattori, si ha p1=q1, p2=q2, …., pr=qr (cioè i fattori coincidono
ordinatamente nelle due fattorizzazioni)
Dimostrazione:
Esistenza della fattorizzazione:
Supponiamo per assurdo che esistano numeri naturali non fattorizzabili nel prodotto di numeri
primi, e costruiamo l’insieme S di tali numeri:
S = {x / xN, x>1, x non é fattorizzabile nel prodotto di numeri primi}
L’insieme non vuoto S, per l’Assioma del minimo, contiene un elemento minimo sS: sarà sN,
s>1, s non fattorizzabile nel prodotto di numeri primi. In particolare s non è un numero primo
(altrimenti s sarebbe fattorizzabile nel prodotto di numeri primi, con 1 solo fattore) quindi s ha un
divisore non banale b, con b1,bs. Esiste allora un naturale c tale che s=bc, e ovviamente anche
c1,cs. In totale si ha 1<b<s, 1<c<s, ed essendo s il minimo in S, si deduce che b,cS, dunque b,c
sono entrambi fattorizzabili nel prodotto di numeri primi, ma allora anche a=bc sarebbe
fattorizzabile nel prodotto di numeri primi, contraddizione.
Unicità della fattorizzazione:
Sia a un numero naturale >1 e siano date 2 fattorizzazioni di a in prodotto di numeri primi:
a=p1p2….pr=q1q2…qs (dove tutti i pi e i qj sono numeri primi)
Le tesi sono allora le seguenti:
1) r=s (il numero dei fattori primi nelle 2 fattorizzazioni è uguale)
2) riordinando opportunamente i fattori, si ha p1=q1, p2=q2, …., pr=qr (cioè i fattori coincidono
ordinatamente nelle due fattorizzazioni).
Dall’eguaglianza a=p1(p2….pr)=q1q2…qs segue che p1 è divisore del prodotto q1q2…qs. Per
l’Osservazione preedente, il numero primo p1 è divisore di almeno uno dei fattori q1,q2,…,qs e,
riordinando opportunamente i fattori, possiamo fare in modo che p1q1. Essendo q1 primo, le
possibilità per il suo divisore p1 sono p1=1 oppure p1=q1. Ma allora p1=q1 (perché per definizione di
numero primo si ha p1>1).
Dividendo ambo i membri dell’eguaglianza per p1 si ottiene l’eguaglianza: p2p3….pr=q2q3…qs, e si
può iterare il ragionamento ottenendo p2=q2 (riordinando di nuovo opportunamente i fattori). La tesi
2) è dunque dimostrata. Dimostriamo ora la tesi 1): se per assurdo la supponessimo falsa, si avrebbe
rs. Supponiamo per esempio che sia r>s (se r<s si ragiona in modo simile): dopo s passi del
precedente procedimento iterativo, dividendo per ps, si avrebbe alla fine l’eguaglianza:
ps+1ps+2….pr=1, contraddizione perché i numeri primi pi sono tutti >1.
Illustriamo 1 conseguenza del Teorema di fattorizzazione unica:
Teorema.
La radice quadrata di un numero primo p è un numero non razionale.
Dimostrazione:
Per assurdo supponiamo p =a/b dove a,b sono naturali. Si ha p=a2/b2, b2p=a2.
Nel caso a=1, si ha b2p=1, contraddizione perché p>1.
Nel caso b=1 si ha p=a2=aa, contraddizione perché il primo p avrebbe un divisore a non banale.
Infine nel caso a>1, b>1, fattorizziamo a, b in prodotto di primi:
a=p1p2….pr , b=q1q2…qs
da cui si avrebbe:
b2p= q1q1q2q2…qsqsp=a2=p1p1p2p2…prpr
e per il Teorema di fattorizzazione unica sarebbe uguale il numero di fattori primi nelle 2
fattorizzazioni, ottenenendo l’eguaglianza 2s+1=2r, contraddizione perché 2s+1 è dispari, 2r è pari.