Esempi di esercizi risolti (statica corpo rigido)
Esempio 1
d
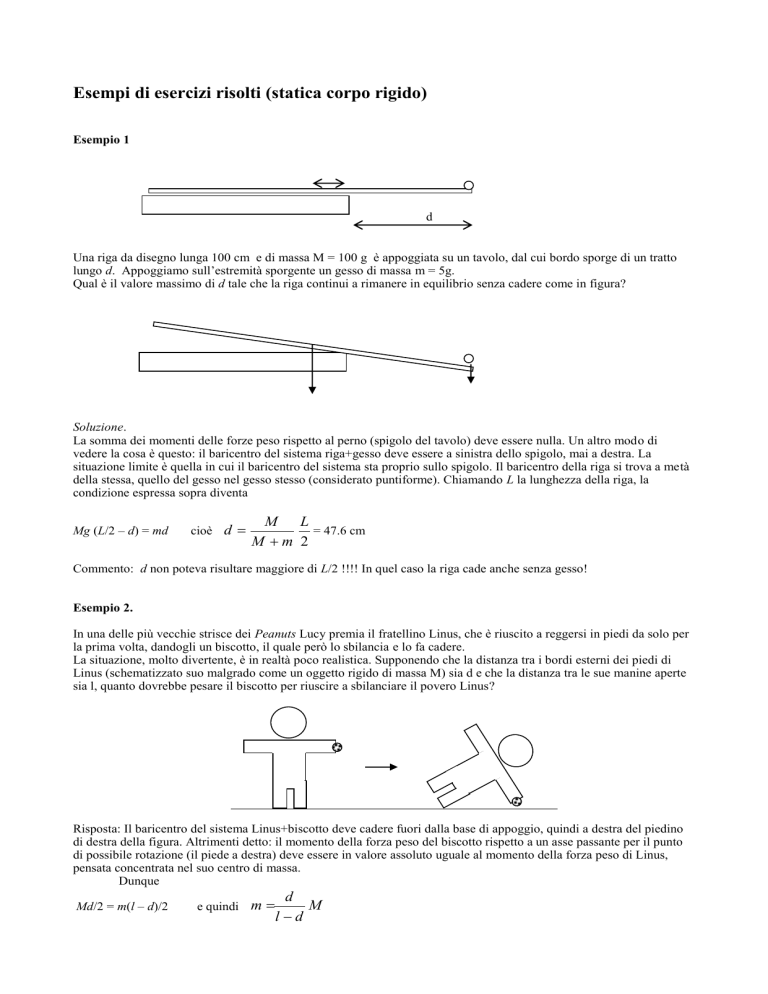
Una riga da disegno lunga 100 cm e di massa M = 100 g è appoggiata su un tavolo, dal cui bordo sporge di un tratto
lungo d. Appoggiamo sull’estremità sporgente un gesso di massa m = 5g.
Qual è il valore massimo di d tale che la riga continui a rimanere in equilibrio senza cadere come in figura?
Soluzione.
La somma dei momenti delle forze peso rispetto al perno (spigolo del tavolo) deve essere nulla. Un altro modo di
vedere la cosa è questo: il baricentro del sistema riga+gesso deve essere a sinistra dello spigolo, mai a destra. La
situazione limite è quella in cui il baricentro del sistema sta proprio sullo spigolo. Il baricentro della riga si trova a metà
della stessa, quello del gesso nel gesso stesso (considerato puntiforme). Chiamando L la lunghezza della riga, la
condizione espressa sopra diventa
Mg (L/2 – d) = md
cioè d
M L
= 47.6 cm
M m 2
Commento: d non poteva risultare maggiore di L/2 !!!! In quel caso la riga cade anche senza gesso!
Esempio 2.
In una delle più vecchie strisce dei Peanuts Lucy premia il fratellino Linus, che è riuscito a reggersi in piedi da solo per
la prima volta, dandogli un biscotto, il quale però lo sbilancia e lo fa cadere.
La situazione, molto divertente, è in realtà poco realistica. Supponendo che la distanza tra i bordi esterni dei piedi di
Linus (schematizzato suo malgrado come un oggetto rigido di massa M) sia d e che la distanza tra le sue manine aperte
sia l, quanto dovrebbe pesare il biscotto per riuscire a sbilanciare il povero Linus?
Risposta: Il baricentro del sistema Linus+biscotto deve cadere fuori dalla base di appoggio, quindi a destra del piedino
di destra della figura. Altrimenti detto: il momento della forza peso del biscotto rispetto a un asse passante per il punto
di possibile rotazione (il piede a destra) deve essere in valore assoluto uguale al momento della forza peso di Linus,
pensata concentrata nel suo centro di massa.
Dunque
Md/2 = m(l – d)/2
e quindi m
d
M
ld
Esempio 3
Una stadera è composta da un’asta rigida, di massa trascurabile, libera di ruotare attorno al perno O che la divide in due
bracci asimmetrici. All’estremità del braccio più corto è appeso il piatto su cui si posa l’oggetto da pesare, mentre
sull’altro braccio si possono spostare un pesino «grande» m 1=100 g e uno «piccolo» m2=10 g.
Il braccio lungo misura a=1 m mentre quello corto misura d=5 cm.
a) Se la bilancia è in equilibrio quando il pesino m1 si trova a distanza x dal perno e m2 a distanza 0, quanto pesa
l’oggetto sul piatto?
b) Se ora aggiungo al piatto una massa m, di quanto devo spostare il pesino piccolo m2?
c) Qual è la massima massa che posso aggiungere riuscendo a pesarla spostando solo il pesino piccolo, lasciando al suo
posto il pesino grande?
Sol.:
a) La bilancia è in equilibro quando i momenti assiali delle forze rispetto all’asse passante per il perno hanno somma
zero (o, alternativamente, quando il baricentro del sistema è sulla verticale rispetto al punto di sospensione).
Il pesino leggero, essendo al punto di sospensione, non contribuisce al conto.
La condizione è espressa da Md = m1x. Dunque
M = m1x/d
b) L’equilibrio dei momenti deve valere di nuovo. Chiamando y la distanza dal punto di sospensione del pesino leggero,
si ha
(M+m)d = m1x + m2y.
Ma siccome Md = m1x, si ottiene md = m2y e quindi
y = md/m2 .
La stessa relazione si ottiene osservando che la bilancia è già in equilibrio con i pesi M e m1. Quindi occorre equilibrare
solo il nuovo momento delle forze aggiunto, quello dovuto alla nuova massa sul piatto (e quindi md = m2y).
c) Il massimo bilanciamento dei momenti che può dare il solo pesino leggero si ottiene quando lo si sposta in fondo al
braccio, cioè per y=a. Dunque se non si vuole spostare l’altro pesino, la massima massa che si può aggiungere al piatto
è tale che md = m2a, cioè
m = m2a/d.
Esempio 4.
Un tizio compra un quadro di dimensioni (base per altezza) 50 cm x 70 cm e, quando lo appende al muro con un
gancetto fissato lungo il lato superiore, osserva che “pende”, formando un angolo di 5 rispetto alla verticale.
a)
Di quanto deve spostare il gancetto lungo il lato superiore della cornice affinché il quadro rimanga dritto
quando viene appeso?
b) Se il quadro ha massa m, base b e altezza h, con che forza deve “spingere” orizzontalmente lo spigolo
inferiore perché il quadro stia dritto, indicando con x lo spostamento del gancetto dalla posizione centrale?
x
h
F
g
b
Soluzione:
a) Il quadro è in equilibrio quando il suo baricentro è sulla verticale rispetto al punto di sospensione.
Il baricentro si trova al centro del rettangolo. I cateti del triangolo mostrato in figura sono dunque
la semialtezza del rettangolo e la distanza del punto di sospensione dal centro della base.
∆x
h/2
Vale dunque
∆x = tan () h/2
b) Il momento totale delle forze rispetto al punto di sospensione deve essere nullo.
La forza peso, applicata nel baricentro, ha un braccio rispetto al punto di sospensione pari a x. Dunque il momento della
forza peso tende a far ruotare il quadro in senso orario e vale in modulo mgx.
La forza applicata tende a far ruotare il quadro in senso antiorario. Il suo braccio è pari a h, dunque il momento vale in
valore assoluto Fh. Se imponiamo che i due momenti siano uguali e opposti essi devono avere lo stesso valore assoluto
e dunque Fh = mgx. La forza deve quindi valere F = mgx/h .