2.2 Il baricentro
2 Geometria delle masse e momento statico
1
2.2.4 Baricentro di figure geometriche regolari
Baricentro di un settore circolare
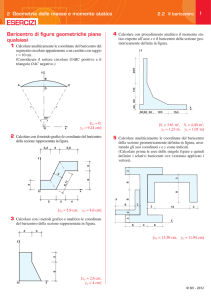
Il settore circolare ammette come asse di simmetria la bisettrice dell’angolo AOB e quindi su di essa giace il baricentro G
[fig. a].
y
M
M’
A
g
g
yG =
G
g4
g
ultime è anche baricentro del settore circolare e giace sull’arco
di circonferenza +
A⬘M⬘B⬘, luogo geometrico dei baricentri g,
per cui il problema è ricondotto alla determinazione del baricentro di un arco di circonferenza.
La posizione del baricentro G viene determinata come indicato in figura a relativamente all’arco+
A⬘M⬘B⬘, con la stessa costruzione grafica, e analiticamente vale la stessa formula
ponendo (2/3) ⋅ r al posto di r, cioè:
3
B
2
2 r ⋅ sen α
⋅
⋅ R⬙
3
α⬙
[1]
Nel caso di un semicerchio [fig. b] la [1] diventa:
1
yG
B’
A’
a
yG =
4 r
⋅
3 π
[2]
2
3 r
r
0
x
y
Fig. a
G
yG
Immaginando di scomporre il settore circolare in settori circolari piccolissimi, ognuno di questi è assimilabile a un triangolo isoscele il cui baricentro g dista dal centro O della
quantità (2/3) ⋅ r; pensando di concentrare nei baricentri g dei
vari triangoli elementari le loro aree, il baricentro di queste
x
Fig. b
© SEI - 2012