2 Geometria delle masse e momento statico
2.2 Il baricentro
1
ESERCIZI
Baricentro di figure geometriche piane
qualsiasi
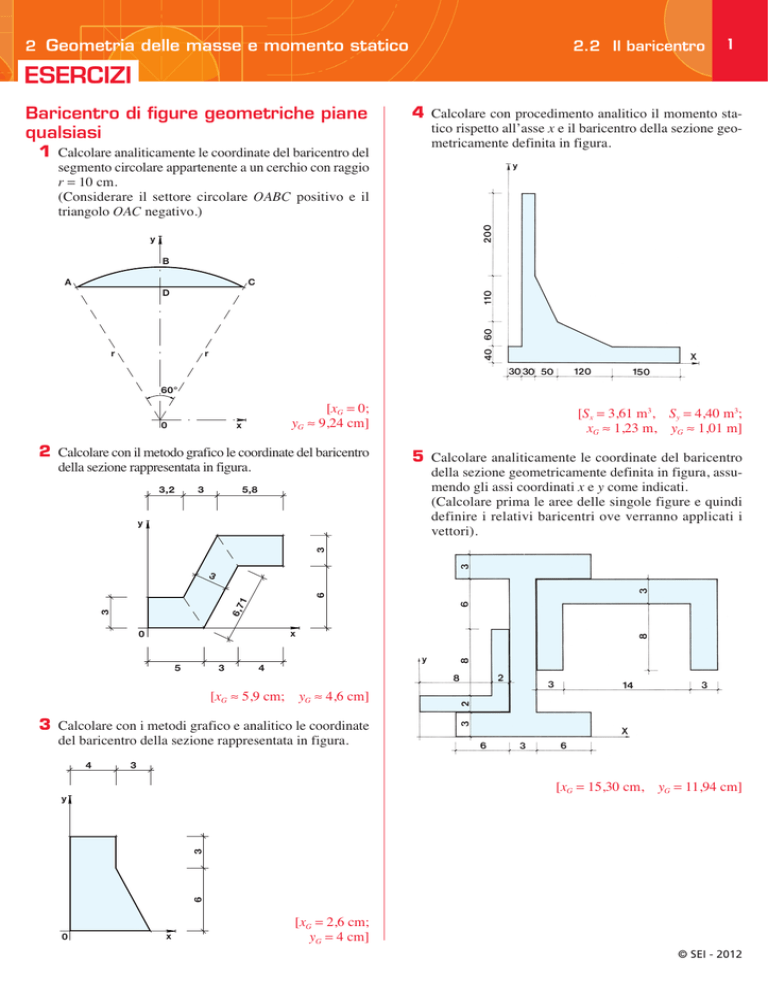
1 Calcolare analiticamente le coordinate del baricentro del
4 Calcolare con procedimento analitico il momento statico rispetto all’asse x e il baricentro della sezione geometricamente definita in figura.
segmento circolare appartenente a un cerchio con raggio
r = 10 cm.
(Considerare il settore circolare OABC positivo e il
triangolo OAC negativo.)
y
B
A
C
D
r
r
60°
[xG = 0;
yG ≈ 9,24 cm]
[Sx = 3,61 m3, Sy = 4,40 m3;
xG ≈ 1,23 m, yG ≈ 1,01 m]
2 Calcolare con il metodo grafico le coordinate del baricentro
5 Calcolare analiticamente le coordinate del baricentro
0
x
della sezione rappresentata in figura.
3,2
3
della sezione geometricamente definita in figura, assumendo gli assi coordinati x e y come indicati.
(Calcolare prima le aree delle singole figure e quindi
definire i relativi baricentri ove verranno applicati i
vettori).
5,8
3
y
3
6,7
1
6
3
x
0
5
3
4
[xG ≈ 5,9 cm; yG ≈ 4,6 cm]
3 Calcolare con i metodi grafico e analitico le coordinate
del baricentro della sezione rappresentata in figura.
4
3
[xG = 15,30 cm, yG = 11,94 cm]
6
3
y
0
x
[xG = 2,6 cm;
yG = 4 cm]
© SEI - 2012
2 Geometria delle masse e momento statico
2.2 Il baricentro
2
6 La sezione composta metallica riportata in figura è co-
7 Calcolare le coordinate del baricentro G della sezione
stituita di profilati in ferro normalizzati collegati con
piastre metalliche.
Si richiede il calcolo analitico del baricentro.
(La posizione del baricentro di ogni profilato e la relativa area sono forniti dalle tabelle delle travi in acciaio
riportate sul Manuale).
riportata in figura, con procedimento analitico, assumendo un sistema di assi cartesiani tangenti ai lati
estremi della figura.
[xG = 6,14 cm, yG = 7,23 cm]
[xG = 11,21 cm, yG = 10,75 cm]
© SEI - 2012